Lineaarisen regression kertoimien tulkinta

Lineaarisen regression kertoimien tulkinta

Tänä päivänä on olemassa lukuisia koneoppimisalgoritmeja, joita voimme kokeilla löytääkseen parhaimman sopivan omaan ongelmaamme. Joillakin algoritmeilla on selkeä tulkinta, toiset taas toimivat mustalaatikkona, ja voimme käyttää LIME:n tai SHAP:n kaltaisia lähestymistapoja joidenkin tulkintojen johtamiseen.

Tässä artikkelissa haluan keskittyä perustavanlaatuisimman regressiomallin eli lineaarisen regression kertoimien tulkintaan, mukaan lukien tilanteet, joissa riippuvaisia/riippumattomia muuttujia on muunnettu (tässä tapauksessa puhun log-muunnoksesta).

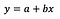
Oletan, että lukija on perehtynyt lineaariseen regressioon (jos ei ole, niin hyviä artikkeleita ja Mediumin viestejä löytyy paljon), joten keskityn pelkästään kertoimien tulkintaan.

Lineaarisen regression peruskaava on nähtävissä yllä (jätin jäännökset tarkoituksella pois, jotta asiat pysyisivät yksinkertaisina ja ytimekkäinä). Kaavassa y tarkoittaa riippuvaista muuttujaa ja x on riippumaton muuttuja. Oletetaan yksinkertaisuuden vuoksi, että kyseessä on yksimuuttujainen regressio, mutta periaatteet pätevät ilmeisesti myös monimuuttujaisessa tapauksessa.

Tulkitaksemme asiaa, sanotaan, että mallin sovittamisen jälkeen saamme:

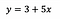
Sisäpiste (a)

Jakaannun leikkauspisteen tulkintaan kahteen tapaukseen:

• x on jatkuva ja keskitetty (kun jokaisesta havainnosta vähennetään x:n keskiarvo, muunnetun x:n keskiarvoksi tulee 0) – keskiarvo y on 3, kun x on yhtä suuri kuin otoskeskiarvo
• x on jatkuva, mutta ei keskitetty – keskiarvo y on 3, kun x = 0
• x on kategorinen – keskiarvo y on 3, kun x = 0 (tällä kertaa osoittaa luokan, tästä lisää jäljempänä)

Kerroin (b)

• x on jatkuva muuttuja

Tulkinta: Yksikön lisäys x:ssä johtaa keskimääräisen y:n kasvuun 5 yksikköä, kun kaikki muut muuttujat pidetään vakiona.

• x on kategorinen muuttuja

Tämä vaatii hieman enemmän selitystä. Oletetaan, että x kuvaa sukupuolta ja voi ottaa arvoja (’mies’, ’nainen’). Muunnetaan se nyt dummy-muuttujaksi, joka ottaa arvot 0 miehille ja 1 naisille.

Tulkinta: Keskimääräinen y on 5 yksikköä suurempi naisilla kuin miehillä, kaikki muut muuttujat pidetään vakiona.

log-tason malli

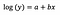
Tyypillisesti käytämme log-muunnosta vetääksemme positiivisesti vinoutuneen jakauman reunimmaista dataa lähemmäs datan enemmistöä, jotta muuttuja saataisiin normaalisti jakautuneeksi. Lineaarisen regression tapauksessa yksi lisähyöty log-muunnoksen käytöstä on tulkittavuus.

Kuten aiemminkin, sanotaan, että alla oleva kaava esittää sovitetun mallin kertoimet.

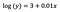
Sisäpiste (a)

Tulkinta on samanlainen kuin vaniljaisessa (tasotason) tapauksessa, mutta tulkintaa varten on kuitenkin otettava eksponenttina sisäpisteen eksponentti exp(3) = 20,09. Erona on se, että tämä arvo tarkoittaa y:n geometrista keskiarvoa (erotuksena aritmeettisesta keskiarvosta tasomallin tapauksessa).

Kerroin (b)

Periaatteet ovat jälleen samankaltaiset kuin tasomallissa, kun kyse on kategoristen/numeeristen muuttujien tulkinnasta. Analogisesti interceptin kanssa meidän on otettava kertoimen eksponentti: exp(b) = exp(0.01) = 1.01. Tämä tarkoittaa, että yksikkökohtainen lisäys x:ssä aiheuttaa 1 %:n lisäyksen keskimääräisessä (geometrisessa) y:ssä, kun kaikki muut muuttujat pidetään vakiona.

Kaksi mainitsemisen arvoista asiaa tässä:

• On olemassa nyrkkisääntö, kun on kyse tällaisen mallin kertoimien tulkinnasta. Jos abs(b) < 0.15 on melko turvallista sanoa, että kun b = 0.1 havaitsemme 10 %:n kasvun y:ssä yksikkömuutosta x:ssä. Suuremmilla absoluuttisilla arvoilla varustetuille kertoimille on suositeltavaa laskea eksponentti.
• Koska kyseessä ovat vaihteluvälillä olevat muuttujat (kuten prosenttiluku), on tulkinnan kannalta kätevämpää ensin kertoa muuttuja 100:lla ja sen jälkeen sovittaa malli. Näin tulkinta on intuitiivisempi, koska kasvatamme muuttujaa yhdellä prosenttiyksiköllä 100 prosenttiyksikön sijasta (heti 0:sta 1:een).

level-log-malli

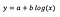
Esitetään, että mallin sovittamisen jälkeen saamme:

Tulkinta leikkauspisteestä on sama kuin tasomallin tapauksessa.

Kertoimen b osalta – 1 %:n kasvu x:ssä johtaa keskimääräisen y:n likimääräiseen kasvuun b/100 (tässä tapauksessa 0,05), kun kaikki muut muuttujat pidetään vakiona. Saadaksemme tarkan määrän, meidän olisi otettava b × log(1,01), mikä tässä tapauksessa antaa 0,0498.

log-log-malli

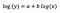
Asetetaan, että mallin sovittamisen jälkeen saamme:

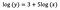
Keskityn jälleen kerran b:n tulkintaan. Kasvu x:ssä 1 %:lla johtaa keskimääräisen (geometrisen) y:n 5 %:n kasvuun, kun kaikki muut muuttujat pidetään vakiona. Saadaksemme tarkan määrän, meidän on otettava

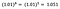
joka on ~5,1 %.

Johtopäätökset

Toivottavasti tämä artikkeli on antanut sinulle yleiskuvan siitä, miten lineaarisen regression kertoimia tulkitaan, mukaan lukien tapaukset, joissa osa muuttujista on log-muunnettu. Kuten aina, kaikki rakentava palaute on tervetullutta. Voit ottaa minuun yhteyttä Twitterissä tai kommenteissa.