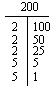Luvut alkulukuina
Kaikki kokonaisluvut luokitellaan joko alkuluvuiksi tai yhdistelmäluvuiksi lukuun ottamatta nollaa ja yhtä, jotka ovat erikoistapauksia. Katsotaanpa, mitä eroa on prime- ja komposiittilukujen välillä. Primaluvuilla on täsmälleen kaksi tekijää, yksi ja itse luku. Jos tunnet jaettavuussäännöt (joita käsitellään seuraavassa jaksossa), alkulukujen 1-100 määrittäminen on suhteellisen helppo tehtävä. Tässä ovat alkuluvut 25:een asti:
2, 3, 5, 7, 11, 13, 17, 19, 23
Kaikkien olemassa olevien alkulukujen löytämiseen ei ole kaavaa, vaikka matemaatikot ovatkin löytäneet alkulukuja, joissa on lähes kahdeksan miljoonaa numeroa. Tämä on yksi jäljellä olevista suurista matemaattisista mysteereistä matemaatikoille.
Yhdysluvuilla on enemmän kuin kaksi tekijää, mutta ei ääretöntä määrää tekijöitä. Kaikki parilliset luvut (lukuun ottamatta lukua kaksi) ovat komposiittilukuja, koska ne kaikki voidaan jakaa kahdella.
Nolla ei ole alkuluku eikä komposiittiluku. Koska mikä tahansa luku kertaa nolla on yhtä kuin nolla, nollan tulolla on ääretön määrä tekijöitä. Yhdistelmäluvulla on oltava äärellinen määrä tekijöitä.
Yksi ei myöskään ole alkuluku eikä yhdistelmäluku. Ainoa tapa saada ykkösen tulo on kertomalla 1 x 1. Mutta kaksoistekijät lasketaan vain kerran, joten ykkösellä on vain yksi tekijä. (Primaariluvulla on täsmälleen kaksi tekijää, joten ykkönen ei voi olla primääri.)
Tyypillisessä testikysymyksessä sinun pitäisi tunnistaa, mikä luku luettelosta on primääri (tai komposiitti tai ei kumpikaan).
Kokeile tätä:
Kysymys
Kuka seuraavista on primääriluku?
- 33
- 45
- 41
- 51
Paljasta vastaus
Oikein vastaus on C. 41 on alkuluku; muut luvut ovat koostettuja. Ole varovainen 51:n kanssa – se tulee 3 x 17:stä.
Viileät säännöt
Jakosäännöt ovat apuvälineitä, jotka auttavat sinua tekemään vähemmän jakoja. Jaettavuussäännöt voivat auttaa sinua määrittämään, onko luku alkuluku vai yhdistetty luku, sekä auttamaan sinua jakamaan yhdistetyt luvut niiden alkutekijöihin, aihetta käsittelemme seuraavaksi.
Divisibiliteettisäännöt ovat oikoteitä, jotka kertovat, onko jokin luku jaollinen toisella luvulla. Säännöt kattavat jakamisen luvuilla 2-10, ja niiden avulla voit tarkistaa luvut aina sataan asti. Napsauta taulukossa olevia numeroita.
| Jakautuvuussäännöt | |||
|---|---|---|---|
| 2 | 3 | 4 | |
| 5 | 6 | 6 | 7 |
| 8 | 9 | 10 | |
Kysymys
Kuka seuraavista luvuista ei ole jaollinen kolmella?
- 4,873
- 7,521
- 12,642
- 25,308
Vastauksen paljastaminen
Oikein vastaus on A. Nopea tapa ratkaista tämä tehtävä on käyttää jaollisuussääntöä; laske yhteen jokaisen luvun numerot etsien sitä lukua, joka ei ole kolmosen kerrannainen. Hidas tapa olisi tehdä jokainen jako-ongelma – jopa laskimella tämä menetelmä kestää kauemmin!
Primäärän kertolasku: T:t ja puu
Tämä on toinen aihe, jota et ehkä ole ajatellut yläasteen jälkeen. Aritmetiikan perusteoriassa sanotaan, että jokainen yhdistetty luku voidaan pilkkoa yksikäsitteiseksi alkulukujen tuotteeksi.
Primitekijöinti on prosessi, jolla löydetään tietyn yhdistetyn luvun alkulukutuotteet. Primfaktorisointi on sinänsä hyödyllistä, mutta monet sen sovellukset liittyvät murtolukuihin, joita käsittelemme myöhemmin.
Voi olla, että pystyt löytämään luvun primfaktorisoinnin mielelläsi. Esimerkiksi 12 on 2 x 2 x 3 tai 22 x 3. (Primfaktorisaatiot esitetään usein eksponenttien avulla.)
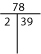
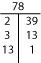
Jos et löydä primfaktorisaatiota henkisesti, kokeile joko Factor-T:tä tai Factor Tree:tä.
Kertaus
- Primaariluvuilla on täsmälleen kaksi tekijää, yksi ja oma itsensä.
- Komposiittiluvuilla on enemmän kuin kaksi tekijää, mutta niitä ei ole ääretön määrä.
- Nolla ja ykkönen eivät ole primetekijöitä eivätkä komposiitteja.
- Jaollisuussäännöt ovat oikoteitä, jotka voivat auttaa lukujen tekijöiden määrittämisessä.
- Jokainen yhdistetty luku voidaan kirjoittaa alkulukujen yksikäsitteisenä tulona, jota kutsutaan luvun alkutekijöinniksi.
- Kaksi kätevää menetelmää alkutekijöintien etsimiseen ovat faktori-T:t ja faktoripuut.