Nelikulmioiden ominaisuudet – suorakulmio, neliö, rinnakkaisneliö, rombi, puolisuunnikas

Nelikulmioiden ominaisuudet – suorakulmio, neliö, rinnakkaisneliö, rombi, puolisuunnikas

Nelikulmio on euklidisessa geometriassa nelikulmio eli nelikulmio on nelisivuinen 2D-kuvio, jonka sisäkulmien summa on 360°. Sana nelikulmio on johdettu kahdesta latinankielisestä sanasta ’quadri’ ja ’latus’, jotka tarkoittavat neljää ja sivua. Siksi nelikulmioiden ominaisuuksien tunnistaminen on tärkeää, kun yritetään erottaa ne muista monikulmioista.

Mitkä ovat siis nelikulmioiden ominaisuuksia? Nelikulmioilla on kaksi ominaisuutta:

• Nelikulmion tulee olla suljettu muoto, jossa on 4 sivua
• Nelikulmion kaikki sisäkulmat ovat yhteensä 360°

Tässä artikkelissa saat käsityksen viidestä nelikulmiotyypistä ja tutustut nelikulmioiden ominaisuuksiin.

Se mitä luet artikkelista:

• Nelikulmioiden eri tyypit
• Suorakulmio
  • Suorakulmioiden ominaisuudet
  • Suorakulmion kaavat
• Neliö
  • Ominaisuudet. neliön
  • Neliön kaavat
• Rinnakkaisneliö
  • Rinnakkaisneliön ominaisuudet
  • Rinnakkaisneliön kaavat
• Rombus
  • Rombuksen ominaisuudet
  • Rombuksen kaavat
• Trapetsin/Trapetsin ominaisuudet
  • Trapetsin ominaisuudet
  • Trapetsin kaavat
• Nelikulmion ominaisuudet
• Tärkeitä nelikulmion kaavoja
• Nelikulmion kysymyksiä

Tässä videossa selitetään nelikulmion ominaisuuksia:

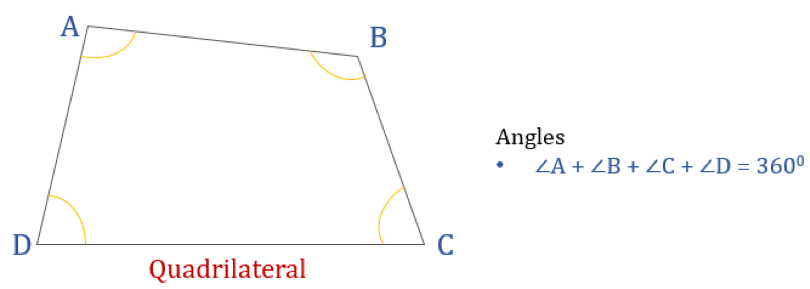
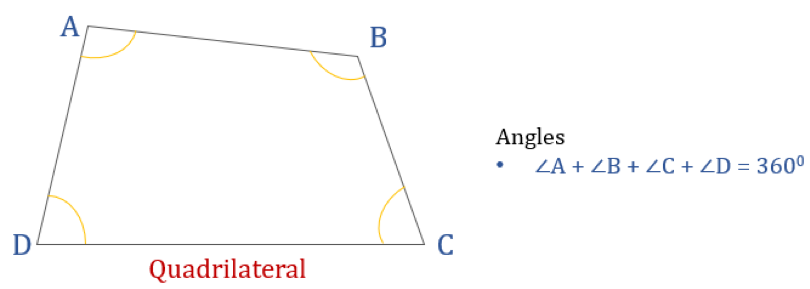
Alla olevassa kaaviossa on nelikulmio ABCD ja sen sisäkulmien summa. Kaikkien sisäkulmien summa on 360°.

Siten ∠A + ∠B + ∠C + ∠D = 360°

Nelikulmioiden eri tyypit

Nelikulmioita on niiden muodon perusteella 5 tyyppiä. Nämä 5 nelikulmiota ovat:

1. Nelikulmio
2. Neliö
3. Parallelogrammi
4. Rombi
5. Trapezio

Keskustellaan jokaisesta näistä viidestä nelikulmiosta yksityiskohtaisesti:

Tässä on kysymyksiä, jotka opettavat sinua soveltamaan kaikkien 5 nelikulmion ominaisuuksia, jotka opit tässä artikkelissa.

Nelikulmio

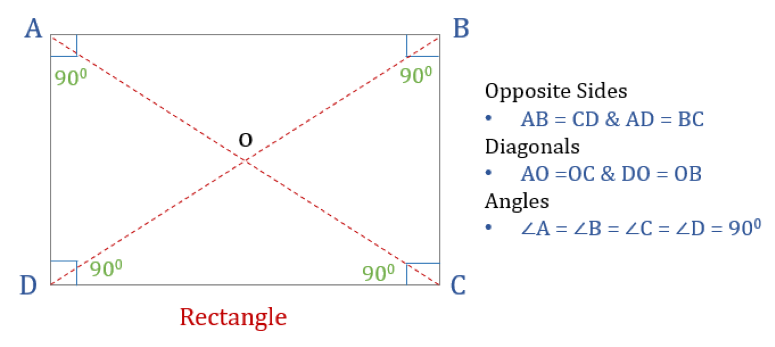
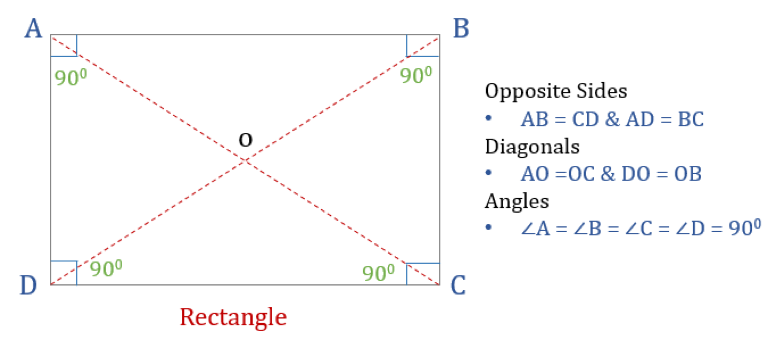
Nelikulmio on nelikulmio, jossa on neljä suoraa kulmaa. Suorakulmion kaikki kulmat ovat siis yhtä suuret (360°/4 = 90°). Lisäksi suorakulmion vastakkaiset sivut ovat yhdensuuntaiset ja yhtä suuret, ja lävistäjät puolittavat toisensa.

Suorakulmion ominaisuudet

Suorakulmiolla on kolme ominaisuutta:

• Suorakulmion kaikki kulmat ovat 90°
• Suorakulmion vastakkaiset sivut ovat yhtä suuret ja yhdensuuntaiset
• Suorakulmion lävistäjät puolittavat toisensa

Suorakulmion kaava – Suorakulmion pinta-ala ja ympärysmitta

Jos suorakulmion pituus on L ja leveys B, niin,

1. Suorakulmion pinta-ala = Pituus × leveys eli L × B
2. Suorakulmion ympärysmitta = 2 × (L + B)

Nämä harjoituskysymykset auttavat sinua vakiinnuttamaan suorakulmion ominaisuuksia

Neliö

Neliö on nelikulmio, jolla on neljä yhtä pitkää sivua ja neljä yhtä pitkää kulmaa. Se on myös säännöllinen nelikulmio, koska sekä sen sivut että kulmat ovat yhtä suuret. Neliössä on suorakulmion tavoin neljä kulmaa, joista kullakin on 90°. Se voidaan nähdä myös suorakulmiona, jonka kaksi vierekkäistä sivua ovat yhtä suuret.

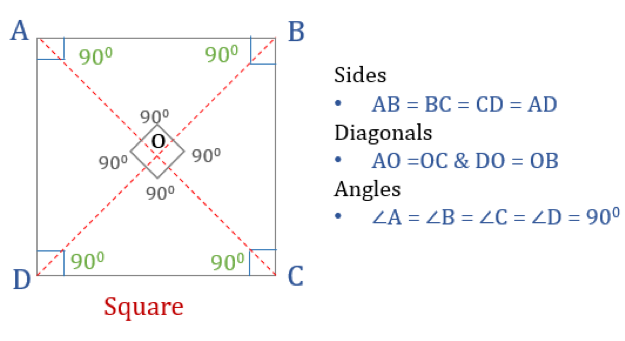
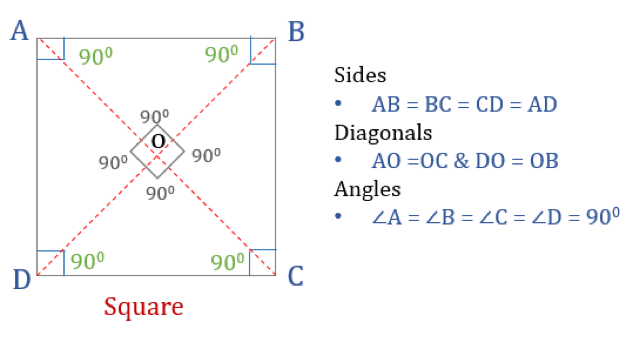
Neliön ominaisuudet

Jotta nelikulmio olisi neliö, sillä on oltava tiettyjä ominaisuuksia. Tässä on kolme neliön ominaisuutta:

• Neliön kaikki kulmat ovat 90°
• Neliön kaikki sivut ovat yhtä suuret ja yhdensuuntaiset
• Lävistäjät puolittavat toisensa kohtisuoraan

Neliön kaava – Neliön pinta-ala ja ympärysmitta

Jos nelikulmion sivu on ’a’, niin,

1. Neliön pinta-ala = a × a = a²
2. Neliön ympärysmitta = 2 × (a + a) = 4a

Nämä harjoituskysymykset auttavat sinua vakiinnuttamaan neliöiden ominaisuuksia

Pistemäärän Q50-51 saavuttaminen GMAT-kokeessa auttaa sinua saamaan GMAT-pistemäärän, joka on yli 700. Mikset alkaisi valmistautua GMAT-kokeeseen ilmaisten valmentautumisresurssiemme avulla ja aloittaisit matkasi saadaksesi Q50-51 GMAT-kokeessa. Opi Carrie Law’lta, joka paransi Q35:stä Q50:een kolmessa viikossa.

Parallelogrammi

Parallelogrammi on nimensä mukaisesti yksinkertainen nelikulmio, jonka vastakkaiset sivut ovat yhdensuuntaiset. Sillä on siis kaksi paria yhdensuuntaisia sivuja. Lisäksi rinnakkaisneliön vastakkaiset kulmat ovat yhtä suuret ja sen lävistäjät puolittavat toisensa.

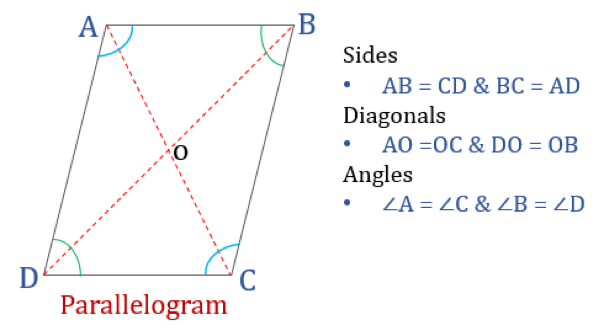
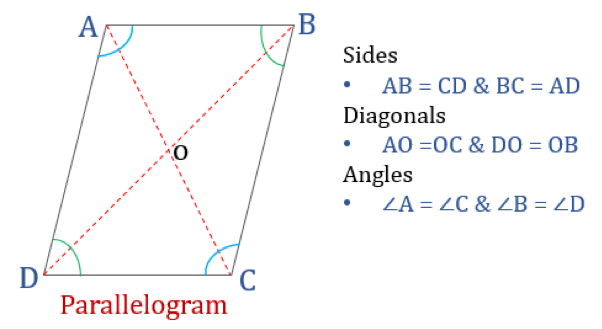
Parallakulmion ominaisuudet

Nelikulmio, joka täyttää alla mainitut ominaisuudet, luokitellaan rinnakkaisneliöksi. Parallelogrammilla on neljä ominaisuutta:

• Vastakkaiset kulmat ovat yhtä suuret
• Vastakkaiset sivut ovat yhtä suuret ja yhdensuuntaiset
• Lävistäjät puolittavat toisensa
• Kahdesta vierekkäisestä kulmasta muodostuva summa on 180°

Parallelogrammin kaavat – Rinnakkaisneliön pinta-ala ja ympärysmitta

Jos samansuuntaisen nelikulmion pituus on ’l’, leveys on ’b’ ja korkeus on ’h’, niin:

1. Parallelogrammin ympärysmitta= 2 × (l + b)
2. Parallelogrammin pinta-ala = l × h

Nämä harjoituskysymykset auttavat sinua vakiinnuttamaan parallelogrammin ominaisuuksia

Rombi

Rombi on nelikulmio, jonka kaikki neljä sivua ovat yhtä pitkiä ja vastakkaiset sivut ovat yhdensuuntaisia. Kulmat eivät kuitenkaan ole yhtä suuria kuin 90°. Rombista, jossa on suorat kulmat, tulisi neliö. Toinen nimitys rombille on ”timantti”, koska se muistuttaa pelikorttien timanttiväriä.

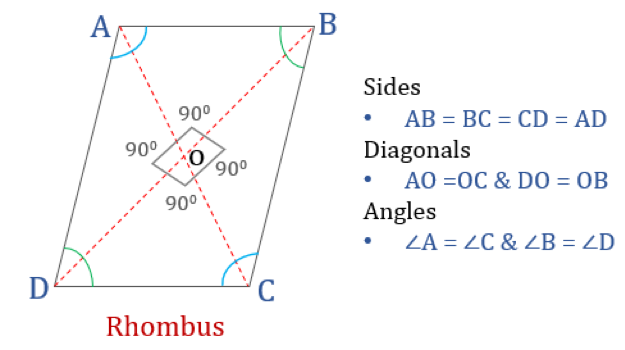
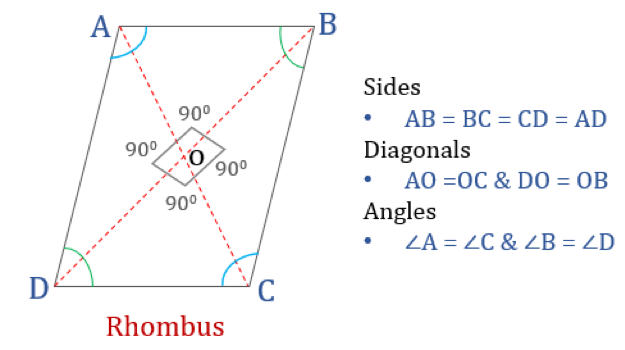
Rombin ominaisuudet

Rombi on nelikulmio, jolla on seuraavat neljä ominaisuutta:

• Vastakkaiset kulmat ovat yhtä suuret
• Kaikki sivut ovat yhtä suuret ja, vastakkaiset sivut ovat toistensa suuntaisia
• Lävistäjät puolittavat toisensa kohtisuoraan
• Kahden vierekkäisen kulman summa on 180°

Rombin kaavat – Rombin pinta-ala ja ympärysmitta

Jos rombin sivu on a niin, rombin ympärysmitta = 4a

Jos rombin kahden lävistäjän pituus on d1 ja d2, niin silloin rombin pinta-ala = ½ × d1 × d2

Nämä harjoituskysymykset ovat auttavat sinua vakiinnuttamaan rombin ominaisuuksia

Trapezium

Trapezium (Yhdysvalloissa Trapezoid) on nelikulmio, jolla on vain yksi pari yhdensuuntaisia sivuja. Yhdensuuntaisia sivuja kutsutaan ’tyvisivuiksi’ ja kahta muuta sivua ’jaloiksi’ tai sivusivuiksi.

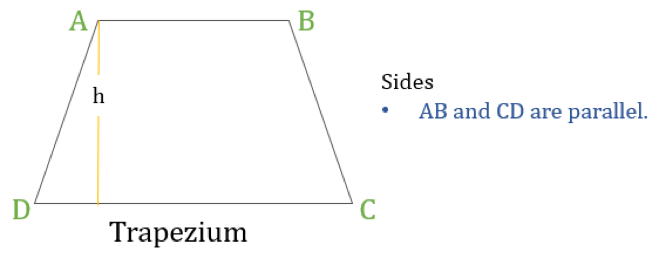
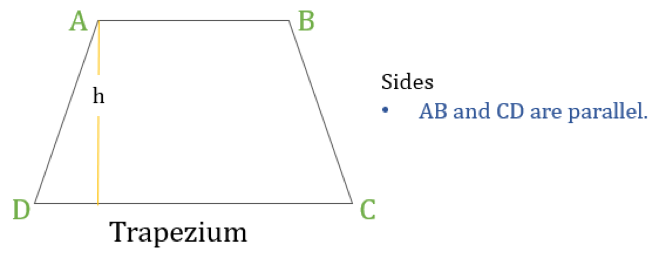
Trapetsin ominaisuudet

Trapetsi on nelikulmio, jolla on seuraava yksi ominaisuus:

• Vain yksi vastakkaisten sivujen pari on yhdensuuntainen

Trapetsin kaavat – Trapetsin pinta-ala ja ympärysmitta

Jos trapetsin korkeus on ’h’ (kuten yllä olevassa kaaviossa on esitetty) niin:

1. Trapetsin ympärysmitta= Kaikkien sivujen pituuksien summa = AB + BC + CD + DA
2. Trapetsin pinta-ala = ½ × (Yhdensuuntaisten sivujen pituuksien summa) × h = ½ × (AB + CD) × h

Tämä… harjoituskysymykset auttavat sinua vakiinnuttamaan trapetsin ominaisuuksia

Nelikulmioiden ominaisuudet

Alla olevaan taulukkoon on koottu yhteen kaikki nelikulmioiden ominaisuudet, jotka olemme tähän mennessä oppineet:

Nelikulmioiden ominaisuudet	Suorakulmio	Neliö	Parallelogrammi	Rombi	Trapezium
Kaikki sivut ovat yhtä suuret	✖	✔	✖	✔	✖
Vastakkain Sivut ovat yhtä suuret	✔	✔	✔	✔	✖
Vastakkain Sivut ovat yhdensuuntaiset	✔	✔	✔	✔	✔	✔
Kaikki kulmat ovat yhtä suuret	✔	✔	✖	✖	✖
Vastakkaiset kulmat ovat yhtä suuret	✔	✔	✔	✔	✖	✖
Kahden vierekkäisen kulman summa on 180	✔	✔	✔	✔	✖
Puolistavat toisiaan	✔	✔	✔	✔	✖
Puolistavat toisiaan kohtisuoraan	✖	✔	✖	✔	✖

Alla olevaan kuvaan on tiivistetty myös nelikulmioiden ominaisuuksia:

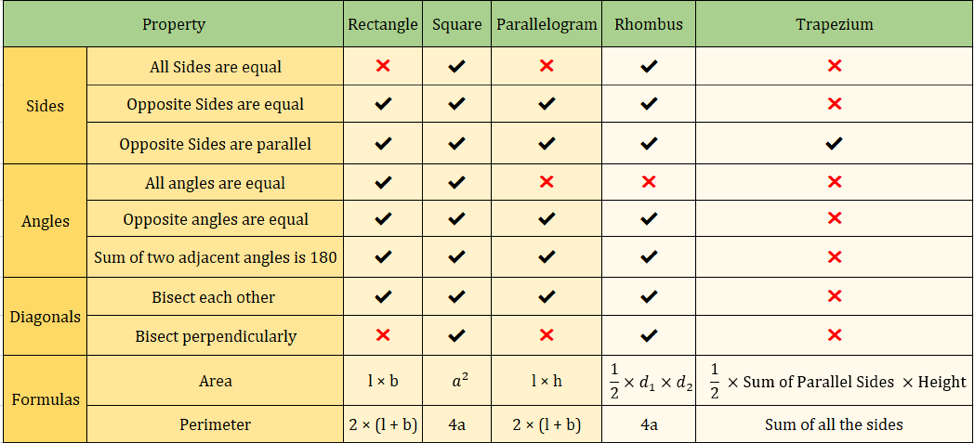
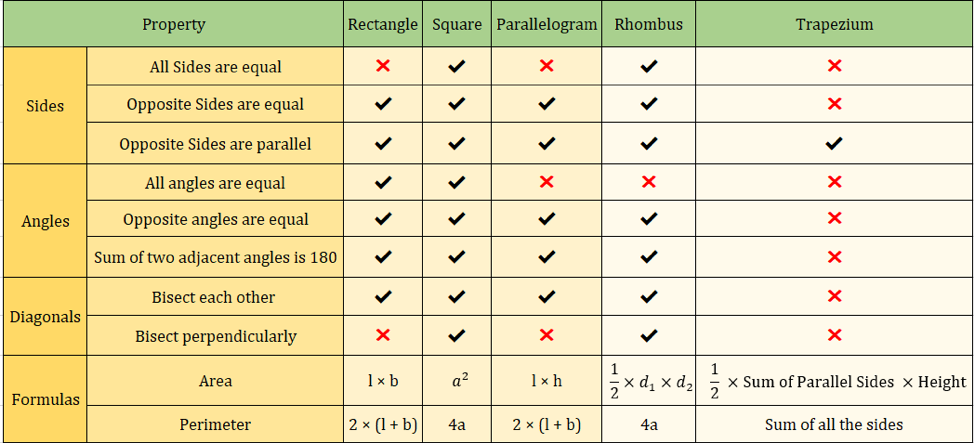
Tärkeitä nelikulmion kaavoja

Alla olevaan taulukkoon on koottu yhteenvetona erilaisten nelikulmioiden pinta-alaa ja ympärysmittaa koskevat kaavat:

Nelikulmion kaavat	Nelikulmio	Neliö	Parallelogrammi	Rhombus	Trapezium
Pinta-ala	l × b	a²	l × h	½ × d1 × d2	½ × (Yhdensuuntaisten sivujen summa) × korkeus
Ympärysmitta	2 × (l + b)	4a	2 × (l + b)	4a	Sivujen summa

Jatkoluku:

• Ympyrän ominaisuudet | Ympyrän kaavat – pinta-ala ja ympärysmitta
• Lukujen ominaisuudet – parillinen & pariton | alkuluku | HCF & LCM
• Kolmioiden ominaisuudet – Määritelmä | Tyypit | Luokittelu
• Suorat ja kulmat – Ominaisuudet ja niiden soveltaminen

Nelikulmiokysymykset

Harjoitellaan nelikulmioiden ominaisuuksien soveltamista seuraavissa esimerkkikysymyksissä:

Kysymys 1

Adam haluaa rakentaa aidan suorakulmaisen puutarhansa ympärille, jonka pituus on 10 metriä ja leveys 15 metriä. Kuinka monta metriä aitaa hänen pitäisi ostaa, jotta hän saisi aidattua koko puutarhan?

1. 20 metriä
2. 25 metriä
3. 30 metriä
4. 40 metriä
5. 50 metriä

Ratkaisu

Vaihe 1: Annettu

• Adamilla on suorakulmainen puutarha.
  • Sen pituus on 10 metriä ja leveys 15 metriä.
  • Hän haluaa rakentaa aidan sen ympärille.

Vaihe 2: Etsitään

• Pituus, joka tarvitaan, jotta koko puutarhan ympärille voidaan rakentaa aita.

Vaihe 3: Lähestyminen ja työstäminen

Aita voidaan rakentaa vain puutarhan ulkosivujen ympärille.

• Tarvittavan aidan kokonaispituus=Puutarhan kaikkien sivujen pituuksien summa.
• Sen vuoksi, että puutarha on suorakaiteen muotoinen, kaikkien sivujen pituuksien summa ei ole mitään muuta kuin puutarhan ympärys.
• Ympärysmitta = 2 × (10 + 15) = 50 metriä

Siten aidan tarvittava pituus on 50 metriä.

Vaihtoehto E on siis oikea vastaus.

Kysymys: 2

Steve haluaa maalata huoneensa yhden suorakulmion muotoisen seinän. Seinän maalaaminen maksaa 1,5 dollaria neliömetriltä. Jos seinä on 25 metriä pitkä ja 18 metriä leveä, mitkä ovat seinän maalaamisen kokonaiskustannukset?

1. $ 300
2. $ 350
3. $ 450
4. $ 600
5. $ 600
6. $ 675

Ratkaisu

Vaihe 1: Annettu

• Steve haluaa maalata huoneensa yhden seinän.
  • Seinä on 25 metriä pitkä ja 18 metriä leveä.
  • Seinän maalaaminen maksaa 1,5 dollaria neliömetriltä.

Vaihe 2: Löytää

• Seinän maalaamisen kokonaiskustannukset.

Vaihe 3: Lähestymistapa ja työstäminen

• Seinä maalataan koko pinta-alaltaan.
  • Jos siis löydämme seinän kokonaispinta-alan neliömetreinä ja kerromme sen kustannuksella maalata 1 neliömetri seinää, niin saamme kokonaiskustannukset.
  • Seinän pinta-ala = pituus × leveys = 25 metriä × 18 metriä = 450 neliömetriä
  • Kokonaiskustannus seinän maalaamisesta = 450 × 1 $.5 = 675 dollaria

Oikein vastaus on siis vaihtoehto E.

Toivomme, että tähän mennessä olisit oppinut nelikulmioiden eri tyypit, niiden ominaisuudet ja kaavat sekä sen, miten näitä käsitteitä sovelletaan nelikulmioita koskevien kysymysten ratkaisemiseen. Nelikulmioiden soveltaminen on tärkeää GMAT-kokeen geometriakysymysten ratkaisemiseksi. Jos suunnittelet GMAT-kokeen suorittamista, voimme auttaa sinua laadukkaalla oppimateriaalilla, jota voit käyttää ilmaiseksi rekisteröitymällä täällä.

Tässä on muutamia muita artikkeleita matematiikasta:

1. Paranna tarkkuutta monikulmioita koskevissa matematiikkakysymyksissä
2. Geometriakysymykset – Yleisimmät virheet | GMAT Quant Prep

Jos suunnittelet osallistuvasi GMAT-kokeeseen, meiltä saat käyttöösi laadukasta verkkosisältöä valmistautumista varten. Olemme gmatclubin arvostelluin GMAT-valmennusyritys yli 1950 arvostelulla.

Mitä jos ottaisit ilmaisen kokeilujakson ja arvioisit itse?

Kirjoita meille osoitteeseen [email protected], jos sinulla on kysyttävää.