Sylinterin pinta-ala – selitys ja esimerkkejä
Katsotaan ensin sylinterin pinta-alaa, ennen kuin siirrytään sylinterin pinta-alaan. Geometriassa sylinteri on kolmiulotteinen hahmo, jolla on kaksi samansuuntaista ympyränmuotoista pohjaa ja kaareva pinta.
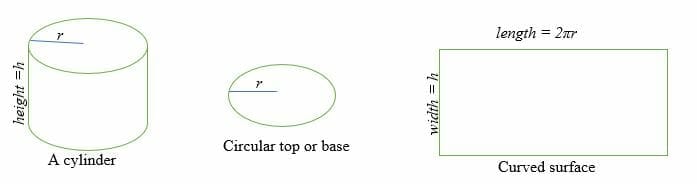
Miten löydetään sylinterin pinta-ala?
Sylinterin pinta-ala on kahden samansuuntaisen ja yhtenevän ympyränmuotoisen pohjan ja kaarevan pinnan pinta-alan summa.
Tässä artikkelissa käsitellään sylinterin kokonaispinta-alan ja sivupinta-alan löytämistä.
Lylinterin pinta-alan laskemiseksi on löydettävä peruspinta-ala (B) ja kaareva pinta-ala (CSA). Sylinterin pinta-ala tai kokonaispinta-ala on siis yhtä suuri kuin peruspinta-alan kerrottuna kahdella ja kaarevan pinnan pinta-alan summa.
Sylinterin kaareva pinta on yhtä suuri kuin suorakulmio, jonka pituus on 2πr ja leveys h.
Missä r = ympyrän sivun säde ja h = sylinterin korkeus.
Kaarevan pinnan pinta-ala = Suorakulmion pinta-ala =l x w = πdh
Pohjapinta-ala, B = Ympyrän pinta-ala = πr2
Lieriön pinta-alan kaava
Lieriön kokonaispinta-alan kaava saadaan seuraavasti:
Lieriön kokonaispinta-ala = 2πr2 + 2πrh
TSA = 2πr2 + 2πrh
Jossa 2πr2 on ympyrän ylä- ja alapinnan pinta-ala ja 2πrh on kaarevan pinnan ala.
Valitsemalla 2πr yhteiseksi tekijäksi RHS:stä saadaan;
TSA = 2πr (h + r) ……………………………………. ……………………………………. (Sylinterin pinta-alan kaava)
Ratkotaan esimerkkitehtäviä, jotka koskevat sylinterin pinta-alaa.
Esimerkki 1
Löydä sellaisen sylinterin kokonaispinta-ala, jonka säde on 5 cm ja korkeus 7 cm.
Ratkaisu
Kaavan
mukaan
TSA = 2πr (h + r)
= 2 x 3.14 x 5(7 + 5)
= 31,4 x 12
= 376,8 cm2
Esimerkki 2
Löydä sellaisen sylinterin säde, jonka kokonaispinta-ala on 2136,56 neliöjalkaa ja korkeus on 3 jalkaa.
Ratkaisu
Annetaan:
TSA = 2136.56 neliöjalkaa
Korkeus, h = 3 jalkaa
Mutta, TSA = 2πr (h + r)
2136.56 =2 x 3.14 x r (3 + r)
2136.56 = 6.28r (3 + r)
Kertolaskun distributiivisen ominaisuuden perusteella RHS:ssä on,
2136.56 = 18.84r + 6.28r2
Jaa jokainen termi 6.28:lla
340.22 = 3r + r2
r2 + 3r – 340,22 = 0 ……… (kvadraattinen yhtälö)
Ratkaisemalla yhtälö kvadraattikaavan avulla saadaan,
r = 17
Siten sylinterin säde on 17 jalkaa.
Esimerkki 3
Lieriönmuotoisen astian maalauskustannukset ovat 0,04 $/cm2. Selvitetään 20 säiliön, joiden säde on 50 cm ja korkeus 80 cm, maalauskustannukset.
Ratkaisu
Lasketaan 20 säiliön kokonaispinta-ala.
TSA = 2πr (h + r)
= 2 x 3.14 x 50 (80 + 50)
= 314 x 130
= 40820 cm2
20 kontin kokonaispinta-ala = 40 820 cm2 x 20
=816 400 cm2
Maalauskustannukset = 816 400 cm2 x 0 $.04 per cm2
= $32 656,
Siten 20 kontin maalauskustannukset ovat $32 656,
Esimerkki 4
Erittäkää sylinterin korkeus, jos sen kokonaispinta-ala on 2552 in2 ja säde 14 in.
Ratkaisu
Annetaan:
TSA = 2552 in2
Säde, r = 14 in.
Mutta, TSA = 2πr (h + r)
2552 = 2 x 3.14 x 14 (14 + h)
2552 = 87,92(14 + h)
Jaa molemmat puolet 87,92:lla, niin saat,
29.026 = 14 + h
Vähennetään molemmilla puolilla 14:llä.
h = 15
Siten sylinterin korkeus on 15 in.
Sylinterin sivupinta-ala
Kuten edellä todettiin, sylinterin kaarevan pinnan pinta-alaa kutsutaan sivupinta-alaksi. Yksinkertaisesti sanottuna sylinterin sivupinta-ala on sylinterin pinta-ala ilman pohjan ja pohjan pinta-alaa (ympyräpinta-ala).
Kaavalla saadaan sylinterin sivupinta-ala;
LSA = 2πrh
Esimerkki 5
Erittäkää sylinterin sivupinta-ala sylinterille, jonka halkaisija on 56 cm ja korkeus 20 cm.
Ratkaisu
Annetaan:
Halkaisija = 56 cm, joten säde, r =56/2 = 28 cm
Korkeus, h = 20 cm
Käytetään kaavaa,
LSA = 2πrh
= 2 x 3.14 x 28 x 20
= 3516,8 cm2.
Siten sylinterin sivupinta-ala on 3516,8 cm2.
Esimerkki 6
Sylinterin sivupinta-ala on 144 ft2. Jos sylinterin säde on 7 ft, etsitään sylinterin korkeus.
Ratkaisu
Annetaan;
LSA = 144 ft2
Säde, r = 7 ft
Säde, r = 7 ft




