Algèbre débutant

Algèbre débutant

Le plan de coordonnées a été développé il y a des siècles (en 1637, pour être exact) et affiné par le mathématicien français René Descartes. En son honneur, le système est parfois appelé le système de coordonnées cartésiennes. Le plan de coordonnées peut être utilisé pour tracer des points et des lignes. Ce système nous permet de décrire des relations algébriques dans un sens visuel, et nous aide également à créer et à interpréter des concepts algébriques.

Les composants du plan de coordonnées

Vous avez probablement déjà utilisé un plan de coordonnées. Par exemple, avez-vous déjà utilisé une superposition quadrillée pour cartographier la position d’un objet ? (Cela se fait souvent avec les cartes routières, aussi.)

Cette « carte » utilise une grille horizontale et verticale pour transmettre des informations sur l’emplacement d’un objet. Remarquez que les lettres A à F sont listées le long du haut, et que les chiffres 1 à 6 sont listés le long du bord gauche. L’emplacement général d’un objet sur cette carte peut être trouvé en utilisant la lettre et le numéro de sa case de grille. Par exemple, vous pouvez trouver l’élément qui existe à la case « 4F » en déplaçant votre doigt le long de l’horizontale jusqu’à la lettre F, puis tout droit vers le bas de façon à être en ligne avec le 4. Vous trouverez qu’un disque bleu se trouve à cet endroit sur la carte.

Le plan de coordonnées comporte des éléments similaires à la grille présentée ci-dessus. Il est constitué d’un axe horizontal et d’un axe vertical, des lignes de nombres qui se croisent à angle droit. (Elles sont perpendiculaires l’une à l’autre.)

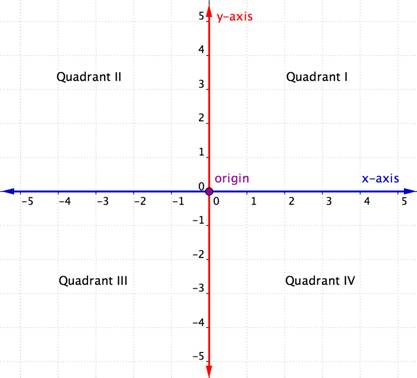
L’axe horizontal du plan de coordonnées est appelé l’axe des x. L’axe vertical est appelé l’axe des y. Le point d’intersection des deux axes s’appelle l’origine. L’origine est à 0 sur l’axe des x et à 0 sur l’axe des y.

Les emplacements sur le plan de coordonnées sont décrits comme des paires ordonnées. Une paire ordonnée vous indique l’emplacement d’un point en mettant en relation l’emplacement du point le long de l’axe des x (la première valeur de la paire ordonnée) et le long de l’axe des y (la deuxième valeur de la paire ordonnée).

Dans une paire ordonnée, telle que (x, y), la première valeur est appelée la coordonnée x et la deuxième valeur est la coordonnée y. Notez que la coordonnée x est listée avant la coordonnée y. Comme l’origine a une coordonnée x de 0 et une coordonnée y de 0, sa paire ordonnée s’écrit (0, 0).

Considérez le point ci-dessous.

Pour identifier l’emplacement de ce point, commencez à l’origine (0, 0) et déplacez-vous vers la droite le long de l’axe des x jusqu’à ce que vous soyez sous le point. Regardez l’étiquette sur l’axe des x. Le 4 indique que, depuis l’origine, vous vous êtes déplacé de quatre unités vers la droite le long de l’axe des x. C’est la coordonnée x. Il s’agit de la coordonnée x, le premier nombre de la paire ordonnée.

De 4 sur l’axe des x, déplacez-vous vers le point et remarquez le nombre avec lequel il s’aligne sur l’axe des y. Le 3 indique qu’après avoir quitté le point, vous êtes passé sous le point. Le 3 indique qu’après avoir quitté l’axe des x, vous avez voyagé de 3 unités vers le haut dans la direction verticale, la direction de l’axe des y. Ce nombre est la coordonnée y. Ce nombre est la coordonnée y, le deuxième nombre de la paire ordonnée. Avec une coordonnée x de 4 et une coordonnée y de 3, vous avez la paire ordonnée (4, 3).

Regardons un autre exemple.

Décrivez le point représenté sous forme de paire ordonnée

Placer des points dans le plan de coordonnées

Maintenant que vous savez comment utiliser les axes x et y, vous pouvez également tracer une paire ordonnée. Rappelez-vous simplement que les deux processus commencent à l’origine – le début ! L’exemple qui suit montre comment représenter graphiquement la paire ordonnée (1,3).

Dans l’exemple précédent, les coordonnées x et y étaient toutes deux positives. Lorsqu’une (ou les deux) des coordonnées d’une paire ordonnée est négative, vous devrez vous déplacer dans la direction négative le long d’un ou des deux axes. Considérez l’exemple ci-dessous dans lequel les deux coordonnées sont négatives.

Les étapes pour tracer un point sont résumées ci-dessous.

Placer des points sur le plan de coordonnées

Identifier les quadrants et les utiliser pour tracer des points

L’intersection des axes x et y du plan de coordonnées le divise en quatre sections. Ces quatre sections sont appelées quadrants. Les quadrants sont nommés à l’aide des chiffres romains I, II, III et IV en commençant par le quadrant supérieur droit et en allant dans le sens inverse des aiguilles d’une montre.

Les paires ordonnées dans un quadrant particulier partagent certaines caractéristiques. Regardez chaque quadrant du graphique ci-dessous. Que remarquez-vous sur les signes des coordonnées x et y des points à l’intérieur de chaque quadrant ?

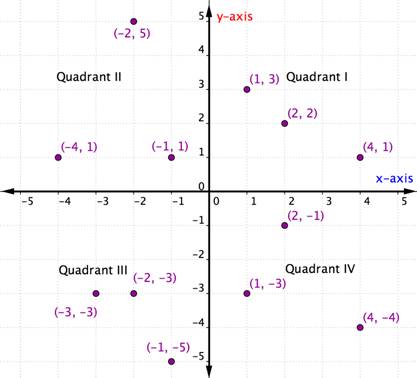
À l’intérieur de chaque quadrant, les signes des coordonnées x et y de chaque paire ordonnée sont les mêmes. Ils suivent également un modèle, qui est décrit dans le tableau ci-dessous.

Quadrant	Forme générale du point dans ce quadrant	Exemple	Description
I	(+,+)	(5,4)	En partant de l’origine, on parcourt l’axe des x dans le sens positif (droite) et l’axe des y dans le sens positif (haut).
II	(-,+)	(-5,4)	En partant de l’origine, on se déplace le long de l’axe des x dans une direction négative (gauche) et le long de l’axe des y dans une direction positive (haut).
III	(-,-)	(-5,-4)	En partant de l’origine, on se déplace le long de l’axe des x dans une direction négative (gauche) et le long de l’axe des y dans une direction négative (bas).
IV	(+,-)	(5,-4)	En partant de l’origine, on se déplace le long de l’axe des x dans une direction positive (droite) et le long de l’axe des y dans une direction négative (bas).

Une fois que vous connaissez les quadrants dans le plan de coordonnées, vous pouvez déterminer le quadrant d’une paire ordonnée sans même la représenter graphiquement en regardant le tableau ci-dessus. Voici une autre façon d’y penser.

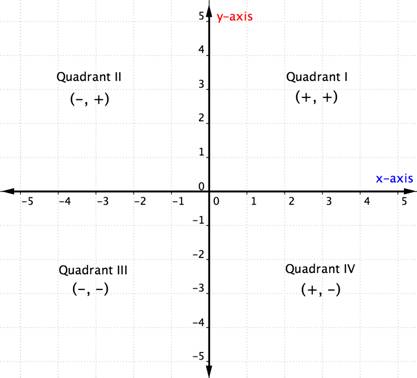
L’exemple ci-dessous détaille comment déterminer l’emplacement du quadrant d’un point juste en pensant aux signes de ses coordonnées. Le fait de penser à l’emplacement du quadrant avant de tracer un point peut vous aider à éviter une erreur. C’est également une connaissance utile pour vérifier que vous avez tracé un point correctement.

Que se passe-t-il si une paire ordonnée a une coordonnée x ou y de zéro ? L’exemple ci-dessous montre le graphique de la paire ordonnée (0,4).

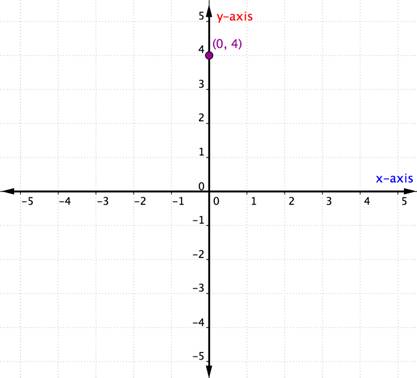
Un point situé sur un des axes n’est pas considéré comme étant dans un quadrant. Il est simplement sur l’un des axes. Chaque fois que la coordonnée x est 0, le point est situé sur l’axe y. De même, tout point dont la coordonnée y est égale à 0 sera situé sur l’axe des x.

Identifier les quadrants et les utiliser pour tracer des points

Résumé

Le plan des coordonnées est un système permettant de représenter graphiquement et de décrire des points et des lignes. Le plan de coordonnées est composé d’un axe horizontal (x-) et d’un axe vertical (y-). L’intersection de ces lignes crée l’origine, qui est le point (0,0). Le plan de coordonnées est divisé en quatre quadrants. Ensemble, ces caractéristiques du système de coordonnées permettent la représentation graphique et la communication des points, des lignes et d’autres concepts algébriques.