Deux façons de diviser les fractions et quelques exemples
Dans ce post, nous allons apprendre à diviser les fractions. Pour ce faire, nous allons nous intéresser à deux méthodes différentes :
Méthode 1 pour diviser des fractions : Multiplication croisée
- Cette méthode consiste à multiplier le numérateur de la première fraction par le dénominateur de la deuxième fraction, puis à écrire la réponse dans le numérateur de la fraction résultante.
- Puis, on multiplie le dénominateur de la première fraction par le numérateur de la deuxième fraction, puis on écrit la réponse dans le dénominateur* de la fraction résultante.
- En dernier lieu, nous simplifions la fraction finale.
Par exemple, pour diviser la fraction
![]()
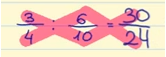
Nous multiplions le numérateur de la première fraction (3) par le dénominateur de la deuxième fraction (10). Cela nous donne le numérateur de la dernière fraction : 3 x 10 = 30.
Puis, nous multiplions le dénominateur de la première fraction (4) par le numérateur de la deuxième fraction (6). Cela nous donne le dénominateur de la dernière fraction : 4 x 6 = 24.
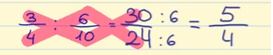
La dernière étape consiste à simplifier la fraction. Comme les deux nombres sont des multiples de 6, nous pouvons diviser le numérateur et le dénominateur par 6.
30 ÷ 6 = 5
24 ÷ 6 = 4
Donc, le résultat de la division est 5/4.
Méthode 2 de division des fractions : Inverser et multiplier
- Étape 1 : inverser la deuxième fraction. C’est-à-dire échanger le numérateur contre le dénominateur.
- Étape 2 : Simplifier tout numérateur avec tout dénominateur.
- Étape 3 : Multiplier à travers.
Par exemple, nous allons diviser :

Étape 1 : Nous inversons la deuxième fraction 6/4. Cela devient 4/6.
Étape 2 : Nous simplifions les numérateurs avec les dénominateurs.
Les numérateurs sont :
12 = 2 x 2 x 3
4 = 2 × 2
Les dénominateurs sont :
5 = 5
6 = 2 × 3
Nous pouvons simplifier à la fois du numérateur et du dénominateur un 2 et un 3. Nous appelons ce processus « annulation croisée » si un numérateur a un facteur commun avec l’autre dénominateur.
Et nous multiplions à travers:
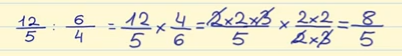
Nous espérons que vous avez aimé ce post.
Si vous voulez voir plus d’exemples, visitez notre post précédent sur les problèmes de mots avec la division des fractions et Comment simplifier les fractions : Fractions de termes inférieurs.
Si vous voulez apprendre beaucoup plus de mathématiques, inscrivez-vous sur Smartick.
En savoir plus :
- Apprendre et pratiquer comment soustraire ou ajouter des fractions
- Apprendre et pratiquer comment multiplier des fractions
- Apprendre comment diviser des fractions avec deux méthodes différentes
- Apprendre comment soustraire. Fractions
- Pratiquez l’addition de fractions avec des exemples



- Auteur
- Postes récents
Une équipe pluridisciplinaire et multiculturelle composée de mathématiciens, d’enseignants, de professeurs et autres professionnels de l’éducation !
Ils s’efforcent de créer le meilleur contenu mathématique possible.
- Exemples de problèmes de mots mathématiques de 3e année avec solutions – 25/03/2021
- Angles intérieurs consécutifs : Ce qu’ils sont et comment les trouver avec des exemples – 03/11/2021
- Exemples de problèmes de mots de CE1 avec solutions – 02/04/2021
.




