Entropie – Le pilier de la thermodynamique et de la théorie de l’information
L’entropie est un terme vague mais puissant qui constitue l’épine dorsale de nombreuses idées clés de la thermodynamique et de la théorie de l’information. Elle a été identifiée pour la première fois par des scientifiques physiques au 19e siècle et a servi de principe directeur pour de nombreuses technologies révolutionnaires de la révolution industrielle. Toutefois, le terme a également contribué à l’avènement de l’ère de l’information lorsqu’il est apparu dans l’ouvrage révolutionnaire du mathématicien Claude Shannon, A Mathematical Theory of Communication. Alors comment un seul terme peut-il être responsable de deux percées, à environ un siècle d’intervalle, dans des domaines connexes mais disparates ?
Premièrement, commençons par la façon dont l’entropie est interprétée dans les sciences physiques. La première loi de la thermodynamique stipule que dans tout système fermé, l’énergie ne peut être ni créée ni détruite. La deuxième loi, également connue sous le nom de loi de l’entropie, stipule que dans un système ouvert, l’énergie passe toujours d’une concentration supérieure à une concentration inférieure afin d’atteindre l’équilibre thermodynamique. Qu’est-ce que cela signifie en pratique ? Cela signifie que votre tasse de café finit par devenir froide et que la glace contenue dans votre boisson fond avec le temps, ou qu’un outil placé dans le feu se réchauffera car l’énergie de la flamme se transfère aux molécules de fer, mais qu’il se refroidira une fois retiré car l’énergie se répartit dans le nouveau milieu environnant.

Le terme entropie lui-même fait référence à l’état de désordre dans un système donné. L’énergie sous une forme concentrée et utilisable est considérée comme ordonnée, tandis que l’énergie sous une forme distribuée et non disponible est considérée comme désordonnée.
L’entropie ne se déplace que dans une seule direction – vers l’équilibre – à moins d’être actionnée par une force extérieure au système, et même dans ce cas, les forces extérieures comme les systèmes biologiques ne réussissent que temporairement à inverser le processus d’entropie et finissent par céder (via la mort). Toute plante ou tout animal est un système énergétique complexe qui survit en contrebalançant le processus entropique et en recueillant de l’énergie disponible et ordonnée dans l’environnement, puis en émettant des déchets dépourvus de nutriments. Mais le débit d’énergie dans le système vivant finit par dégrader sa structure physique, ce qui fait que l’organisme se décompose et meurt (en espérant avoir atteint son but ultime de reproduction). Le corps d’énergie, qui ne vit plus, se décompose et se dissipe dans le milieu environnant – et l’équilibre thermodynamique.
Théoriquement, l’entropie ne cessera sa marche régulière que lorsqu’elle aura provoqué la mort thermique de l’univers – un état final ultime où il n’y a plus d’énergie libre. Tout ce qui se trouve sur terre et dans l’espace finira par se dilater, exploser, mourir et distribuer l’énergie libre de manière uniforme dans ce qui est vraiment le plus grand système fermé de tous : l’univers. De cette façon, l’entropie est une loi universelle semblable à la gravité, car elle opère à la fois aux plus petites et aux plus grandes échelles de la biophysique.
Les économies sont des organismes, pas des machines à laver
L’entropie s’applique également à l’économie. Le processus d’entropie au sein d’un organisme, en acquérant l’énergie disponible dans le milieu environnant et en la transformant en énergie désordonnée, est également vrai pour les groupes d’organismes. Les sociétés prennent des sources d’énergie à faible entropie sous deux formes : les stocks et les flux. Les stocks comprennent les minéraux de terres rares, les combustibles fossiles et d’autres dépôts terrestres créés par des processus terrestres complexes et à long terme au cours des millénaires. Les flux proviennent de ce que l’on considère comme des sources renouvelables, comme le vent, l’eau et l’énergie solaire, qui incluent également la biomasse (en tant qu’extension indirecte de l’énergie solaire). Compte tenu de la nature de chaque source, les stocks sont limités en quantité alors que les flux sont limités à la fois en taux et en quantité. Les civilisations, comme les organismes, ont des métabolismes. Elles traitent l’énergie.

La révolution industrielle a fait passer l’apport énergétique primaire de l’économie des flux aux stocks terrestres pour la première fois. Les charrues à cheval et les voiles à vent, deux formes de travail dépendant des flux, ont été remplacées par l’agriculture mécanisée et les navires à vapeur, qui dépendent des combustibles fossiles. Nous avons capitalisé sur l’énergie solaire dormante fossilisée pendant des millions d’années pour libérer la civilisation des contraintes des flux terrestres biologiques et créer une croissance vertigineuse de la population et du PIB.
Malgré les avantages économiques et matériels indéniables de ce changement, il a eu pour effet secondaire d’accélérer le processus d’entropie et d’accroître le désordre dans le système climatique. Bien que la quantité totale d’énergie reste inchangée à travers le processus économique (à l’exception de l’énergie solaire), l’extraction de minéraux et la consommation de combustibles fossiles nécessaires au processus de production caractérisent un changement qualitatif qui fait passer l’énergie de l’ordre au désordre. De cette façon, l’entropie constitue la base de la rareté parce que les humains ne peuvent pas déplacer l’énergie dans l’autre sens, d’un état de désordre à un état d’ordre ; sans entropie, il serait physiquement possible de retransformer le CO2 atmosphérique en un morceau de charbon, tout comme il serait possible de capturer et de reconfigurer les particules de caoutchouc perdues lorsqu’un pneu se dégrade sur la chaussée.

En fin de compte, notre économie utilise des choses et de l’énergie. Même si l’argent, notre représentation de la valeur, circule indéfiniment dans l’économie, les biens physiques qu’il représente sont soumis à la loi de l’entropie. Le système économique actuel est comme un organisme qui se développe indéfiniment. Notre cœur pompe notre sang et nous maintient en vie, mais cette force use nos cellules avec le temps. Nous vieillissons et nous nous dégradons.
Alors, comment l’entropie s’applique-t-elle à la science des données ?
Maintenant que nous avons jeté un coup d’œil à la façon dont l’entropie se réfère à l’énergie, voyons comment elle s’applique à la communication et à la théorie de l’information. Je pense que cet extrait de la biographie de Claude Shannon par Jimmy Soni et Rob Goodman, A Mind at Play, est une excellente histoire anecdotique des origines de l’entropie :
Shannon a approché le grand homme avec son idée d’information en tant qu’incertitude résolue – qui viendrait à se tenir au cœur de son travail – et avec une question sans prétention. Comment devrait-il appeler cette chose ? Von Neumann a répondu immédiatement : « Disons que l’information réduit l' »entropie ». D’abord, c’est un bon mot de physique, solide. Et surtout, poursuivit-il, personne ne sait ce qu’est réellement l’entropie, donc dans un débat, vous aurez toujours l’avantage. »

Avant de s’attaquer à la définition de l’entropie par Shannon, il peut être utile de décomposer sa définition de l’information. L’idée de base de la théorie de Shannon est que la valeur informative d’un message communiqué dépend de la mesure dans laquelle le contenu du message est surprenant. Un excellent exemple de cette théorie dans la pratique est l’utilisation de la fréquence des lettres dans le langage. D’un point de vue probabiliste, si l’instance d’une lettre est un événement, alors l’issue la plus probable de chaque événement donné suit cette distribution de probabilité :
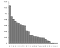
Plus il y a de lettres, moins le message est incertain. Mais cela dépend aussi de la rareté de la lettre. Par exemple, lequel des messages suivants contient le plus d’informations, 1 ou 2 ?
_AT
L’option « 1 » comprend deux lettres avec des probabilités relativement élevées, où vous pouvez épeler toutes sortes de mots en remplissant la lettre manquante : « Chauve-souris », « Chat », « Chapeau », « Gros », « Sat », etc. L’option 2 comprend la lettre « H », comparativement insaisissable, qui offre quelques possibilités de mots restants comme « Chapeau » ou « Frappe », mais pas autant que l’option 1. Par conséquent, l’option 2 communique plus d’informations parce qu’elle réduit l’incertitude à un plus haut degré.
Donc, si l’information est une incertitude résolue, l’entropie doit être l’incertitude qui doit être résolue. La rareté d’un événement, ou sa « surprise », détermine son contenu en information (si vous avez déjà joué au Scrabble, vous savez combien les options seraient limitées si nous tirions la lettre « Q »). Chaque fois que nous communiquons un élément d’information, l’entropie globale, le désordre, l’incertitude ou tout autre terme que vous souhaitez utiliser diminue d’une quantité ou d’un taux proportionnel. Alors, quelle est cette quantité proportionnelle ?
Shannon a calculé que la mesure de l’entropie de l’information associée à chaque valeur possible des données est le logarithme négatif de la fonction de masse de probabilité de cette valeur :
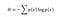
L’entropie mesure la quantité attendue d’information transmise en identifiant le résultat d’un événement aléatoire, où les résultats possibles sont une fonction de probabilité. Cela implique que le lancer d’un dé a une entropie plus élevée que le lancer d’une pièce de monnaie, car chaque résultat du lancer d’un dé (⅙) a une probabilité plus faible que de tomber sur pile ou face (½). Regarder la relation graphiquement aide:

En communiquant un résultat de pile, on sait que pile n’a pas eu lieu.
En apprentissage automatique, l’interprétation mathématique de l’entropie est utilisée pour calculer une métrique de gain d’information pour de nombreux algorithmes. Les arbres de décision, par exemple, sélectionnent l’un des nombreux attributs différents, également appelés caractéristiques ou variables indépendantes, pour diviser de manière répétée les échantillons en sous-ensembles. À chaque division, l’algorithme sélectionne un attribut pour diviser l’échantillon sur, et continue à le faire jusqu’à ce que tous les sous-ensembles soient purs, ou en d’autres termes, chaque échantillon individuel dans un sous-ensemble partage la même classification ou valeur cible.
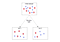
Pour mesurer la pureté d’un sous-ensemble d’échantillons, l’algorithme a besoin d’une mesure quantitative pour choisir objectivement la caractéristique sur laquelle il doit se diviser à chaque nœud donné. C’est là que l’entropie intervient. À chaque étape, l’algorithme calcule l’attribut qui présentera le gain d’information le plus élevé, puis décide de la division. Il calcule également la diminution attendue de l’incertitude avant et après la division ; si elle diminue, la division est retenue et l’algorithme passe à l’étape suivante. Si elle n’a pas diminué, il a atteint la pureté et il se repose. De cette façon, il est responsable à la fois de la sélection de la caractéristique sur laquelle il faut fractionner ainsi que de l’arrêt du processus.
Y a-t-il un lien entre la thermodynamique et la théorie de l’information ?
L’entropie s’écoule inexorablement dans un arbre de décision tout comme elle s’écoule inexorablement dans l’air à travers une tasse de café. Dans l’énergie, elle marche vers l’équilibre thermodynamique ; dans la théorie de l’information, elle marche vers la pureté.
Au fond, l’interprétation énergétique de l’entropie et l’interprétation de la théorie de l’information de l’entropie convergent vers le même point – les lois fondamentales de la physique. La communication nécessite de l’énergie, et l’utilisation de l’énergie nécessite une communication. Selon Shannon, la valeur de l’entropie d’un élément d’information fournit une limite absolue à la longueur moyenne la plus courte possible d’un message, ou à la mesure dans laquelle il peut être compressé, sans perdre d’informations lors de sa transmission. Les semi-conducteurs, les lampes de poche et le fait de taper sur une casserole en morse nécessitent de l’énergie humaine, et nos communications s’efforceront toujours de trouver le moyen de transmission le plus efficace.
Dans le domaine de l’énergie, nous essayons de minimiser l’entropie en limitant la quantité que nous consommons et l’efficacité de notre consommation. Notre objectif est de trouver des sources d’énergie ordonnées et de résister à l’influence de l’entropie sur notre corps. Dans le domaine des communications, nous minimisons l’entropie en trouvant des informations et en réduisant l’incertitude. D’une certaine manière, en réduisant le désordre par la communication, nous pouvons arrêter le processus entropique de l’énergie ; un chasseur-cueilleur peut utiliser le langage pour communiquer avec un autre afin de l’avertir qu’il risque d’être dévoré par un lion, réduisant ainsi l’incertitude 1. de l’endroit où se trouve le lion (entropie de l’information) et 2. du processus d’être dévoré par un lion (entropie de l’énergie). Cet acte de communication réduit l’espace de probabilité de tous les événements possibles et nous permet d’agir de manière plus efficace et efficiente. Comprendre la nature du fonctionnement de cette loi puissante dans les domaines numérique et physique est essentiel pour comprendre les liens entre la thermodynamique et l’ère de l’information.




