Lexique des pompes centrifuges
Les pertes de charge résultent du frottement des parois dans tous les types de canalisations et de la résistance locale à l’écoulement, par exemple dans les vannes et les raccords (voir également Perte de charge).
Vitesses d’écoulement recommandées
- Pour l’eau froide:
La ligne d’aspiration 0.7-1,5 m/s
La ligne de décharge 1,0-2,0 m/s - Pour l’eau chaude:
La ligne d’aspiration 0,5-1,0 m/s
La ligne de décharge 1,5-3,5 m/s
L’équation de la perte de charge d’un écoulement dans une longueur droite de tuyauterie à section circulaire est :
λ Facteur de friction de la conduite
L Longueur de la conduite en m
d Diamètre intérieur de la conduite en m
v Vitesse d’écoulement dans une section transversale en m/s
(= 4 Q / π d2 avec Q en m3/s)
g Accélération due à la gravité en m/s2
voir Fig. 1 et 4 Perte de charge
Le facteur de friction de la conduite a été établi expérimentalement. Il dépend uniquement de l’état d’écoulement du fluide manipulé et de la rugosité relative (d/k) des tuyaux dans lesquels circule le fluide. Pour les sections transversales de tuyaux non circulaires, le diamètre équivalent en termes fluido-mécaniques (d) s’applique:
A Section transversale en m2
U Circonférence de la section mouillée en m
(la surface libre d’un canal ouvert n’est pas considérée)
L’état de l’écoulement est déterminé par le nombre de Reynolds (Re) selon les lois d’affinité. Ce qui suit s’applique aux tuyaux circulaires :
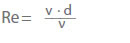
v Vitesse d’écoulement dans une section transversale en m/s
(= 4 Q / π d2 avec Q en m3/s)
ν Viscosité cinématique en m2/s
(pour l’eau à 20 °C : 1.00 – 10 – 6 m2/s)
d Diamètre intérieur du tuyau en m
Voir Fig. 4 Perte de charge
Pour les tuyaux hydrauliquement lisses tels que les tuyaux en métal étiré lisse ou en plastique (par exemple PE ou PVC), ou dans le cas d’un écoulement laminaire, le facteur de friction du tuyau (λ) peut être calculé. Pour un écoulement laminaire dans un tuyau avec un nombre de Reynolds inférieur à 2320, le facteur de friction du tuyau est indépendant de la rugosité :
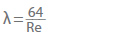
Si l’écoulement est turbulent, ou si le nombre de Reynolds est supérieur à 2320, le facteur de friction du tuyau dans les tuyaux hydrauliquement lisses peut être représenté par une équation empirique selon Eck (en raison du fait que les écarts sont inférieurs à 1 % si le nombre de Reynolds est inférieur à 108).
Le facteur de friction du tuyau (λ) dépend également d’un autre paramètre sans dimension, c’est-à-dire de la rugosité relative de la surface interne du tuyau (d/k). Les deux doivent être spécifiés dans la même unité (par exemple en mm).
Voir Fig. 1 Perte de charge
(k) est la rugosité absolue moyenne de la surface interne du tuyau pour laquelle des valeurs approximatives sont disponibles en fonction du matériau et des procédés de fabrication. Voir Fig. 2 Perte de charge
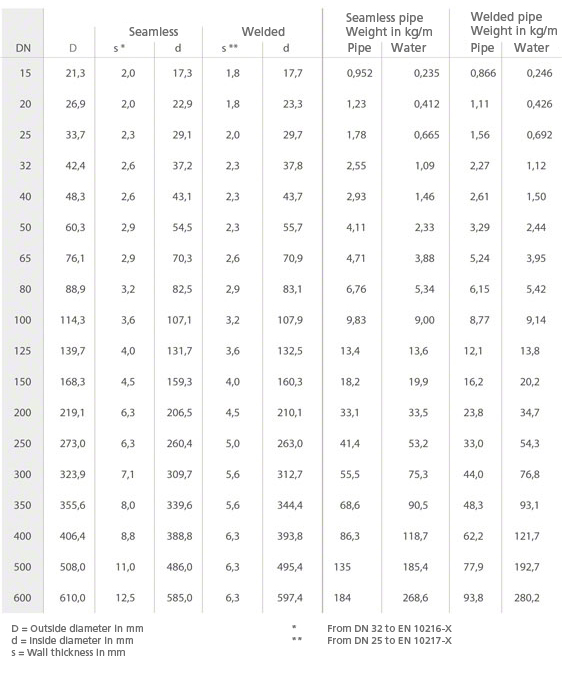Fig. 2 Perte de charge : Estimations des hauteurs moyennes de crête à vallée k (rugosité absolue) des tuyaux
Au-dessus de la courbe limite, le facteur de friction du tuyau (λ) dépend uniquement de la rugosité relative du tuyau (d/k). Voir Fig. 1 Perte de charge
L’équation empirique suivante de Moody peut être utilisée pour cette région :
Pour une utilisation pratique, la perte de charge (HL) par 100 m de tuyau droit en acier est indiquée dans le diagramme en fonction du débit (Q) et du diamètre intérieur du tuyau (d).
Voir Fig. 3 Perte de charge
Les valeurs ne sont valables que pour de l’eau froide et propre ou pour des fluides ayant la même viscosité cinématique, pour des tuyaux complètement remplis et pour une rugosité absolue de la surface intérieure du tuyau de k = 0.05 mm.
Dimensions, poids, remplissage en eau pour des tuyaux neufs en acier sans soudure ou soudés longitudinalement
Voir Annexe, Perte de charge, Fig. 4
L’effet d’une rugosité de surface accrue k sera démontré dans ce qui suit pour un ensemble de plages de paramètres fréquemment utilisées (diamètre nominal DN = 50 à 300, vitesse d’écoulement v = 0,8 à 3,0 m/s). Voir Fig. 3 Perte de charge
La région bleu clair correspond à la région marquée de manière similaire pour une rugosité moyenne absolue de k = 0,05 mm.
Voir Fig. 1 Perte de charge
Pour une rugosité augmentée d’un facteur 6 (tuyau en acier ancien légèrement incrusté avec k = 0,30 = 300 μm (0.30 mm), les facteurs de friction des tuyaux (et les pertes de charge proportionnelles associées) dans la région bleu foncé ne sont que de 25 à 60 % plus élevés qu’auparavant.
Voir Fig. 1 Perte de charge
Pour les canalisations d’eaux usées, l’augmentation de la rugosité causée par l’encrassement doit être prise en considération. Pour les conduites soumises à une incrustation extrême, la perte de charge réelle ne peut être déterminée qu’expérimentalement. Les écarts par rapport au diamètre nominal modifient considérablement la perte de charge, car le diamètre intérieur du tuyau figure dans l’équation à la 5e puissance.
Une réduction de 5 % du diamètre intérieur, par exemple, entraîne une augmentation de la perte de charge pouvant atteindre 30 %. Il est donc important que le diamètre intérieur ne soit pas simplement remplacé par le diamètre nominal dans les calculs.
Les pertes de charge dans les tuyaux en plastique ou les tuyaux métalliques étirés lisses sont très faibles grâce aux surfaces lisses des tuyaux. Les pertes de charge établies sont valables pour de l’eau à 10 °C. À d’autres températures, la perte pour les tuyaux en plastique doit être multipliée par un facteur de correction de température spécifié pour tenir compte de leur plus grande expansion thermique. Pour les eaux usées ou d’autres eaux non traitées, une perte de charge supplémentaire de 20 à 30 % doit être prise en compte pour les dépôts potentiels.
Pertes de charge pour les tuyaux en plastique et les tuyaux métalliques étirés lisses
Voir annexe, perte de charge, Fig. 5
Pertes de charge dans les vannes et les raccords
La perte de charge (HL) dans les vannes et les raccords est donnée par :
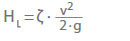
ζ Coefficient de perte
Voir Fig. 6 à 12 Perte de charge
v Vitesse d’écoulement dans une section caractéristique A
(par exemple à la buse) en m/s
g Accélération due à la gravité 9,81 m/s2
Fig. 6 Perte de charge : Schéma de conception des vannes
Fig. 11 Perte de charge : Influence sur le coefficient de perte ζ de l’arrondissement des côtés intérieur et extérieur des coudes dans les conduits carrés
Fig. 12 Perte de charge : Coefficients de perte ζ pour les vannes papillon, à soupape et à opercule en fonction du degré d’ouverture
Les pertes imputables au redressement des perturbations de l’écoulement sur une longueur de conduite équivalente à 12 x DN en aval de la vanne sont incluses dans les coefficients de perte conformément à la directive VDI/VDE 2173. Les valeurs s’appliquent à des vannes dont le débit d’approche est constant, qui sont complètement ouvertes et qui fonctionnent avec de l’eau froide. Selon les conditions d’écoulement d’entrée et de sortie, les modèles de vannes et les objectifs de développement (c’est-à-dire des vannes peu coûteuses ou économes en énergie), les valeurs de perte peuvent varier considérablement. Voir Annexe, Perte de charge, Fig. 7
Souvent la valeur kv est utilisée à la place du coefficient de perte (ζ) lors du calcul de la perte de pression pour l’eau dans les vannes:
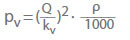
La valeur kv est le débit en m3/h qui résulterait d’une chute de pression pv = 1 bar à travers la vanne pour l’eau froide. Elle décrit la corrélation entre la perte de pression (pL) en bar et le débit (Q) en m3/h. Conversion en coefficient de débit ζ pour l’eau froide:
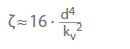
d Diamètre (nominal) de référence de la vanne en cm
Pour le calcul des pertes de charge dans les raccords, les raccords de dérivation et les adaptateurs nécessitent une approche différente. Voir les figures 9 et 10 Perte de charge
Fig. 9 Perte de charge : Coefficients de perte ζ pour les raccords 
Fig. 10 Perte de charge : Coefficients de perte ζ pour les adaptateurs
Pour tous les raccords, il faut différencier deux formes de perte de charge :
- Pertes de charge irréversibles (réduction de la pression)
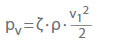
pv Perte de charge en Pa
ζ Coefficient de perte
ρ Densité en kg/m3
v Vitesse d’écoulement dans une section transversale en m/s
.section en m/s
- Variations de pression réversibles de l’écoulement sans frottement selon l’équation de Bernoulli
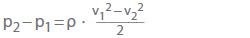
Pour les écoulements accélérés tels que les réductions du diamètre du tuyau, (p2 – p1) est toujours négatif ; pour les écoulements décélérés tels que les dilatations des tuyaux, il est toujours positif. Lorsque l’on calcule la variation nette de pression comme la somme arithmétique de pL et de (p2 – p1), il faut toujours soustraire les pertes de pression irréversibles.
Influence des fluides hautement visqueux sur la courbe caractéristique du système
Comme les lois de la dynamique des fluides conservent leur validité pour tous les fluides newtoniens, les équations et les diagrammes de calcul des facteurs de friction des tuyaux et des coefficients de perte pour les vannes sont également applicables aux fluides visqueux dont la viscosité est supérieure à celle de l’eau.
Lors du calcul du nombre de Reynolds Re = v – d / ν , il faut simplement substituer la viscosité cinématique des fluides visqueux νz à la viscosité de l’eau νz.
On obtient ainsi un nombre Re plus faible et, d’après la figure 1 Perte de charge, un coefficient de frottement de la conduite plus grand λz (Note : l’influence de la rugosité de la paroi peut maintenant souvent être ignorée en raison de la plus grande épaisseur de la couche limite dans l’écoulement).
Toutes les pertes de charge dans les conduites et les vannes calculées pour l’eau doivent être extrapolées en utilisant le rapport λz/λw.
La figure 13 Perte de charge convient également à une utilisation pratique générale : le coefficient de frottement de la conduite λz peut être déterminé rapidement en fonction du débit Q, du diamètre intérieur d de la conduite et de la viscosité cinématique νz. Il faut cependant garder à l’esprit que le coefficient λw dans ce diagramme n’est valable que pour les tuyaux hydrauliquement lisses (c’est-à-dire pas pour les tuyaux rugueux) ! Le λw correspondant peut être utilisé pour calculer le rapport λz/λw.
Comme la composante statique de la courbe caractéristique du système Hsys , voir Fig. 1 Courbe caractéristique du système et Fig. 2 Tête, n’est pas affectée par la viscosité, la composante dynamique de la courbe caractéristique du système pour l’eau peut être redessinée comme une parabole plus raide pour un fluide visqueux.
Influence des fluides non newtoniens sur la courbe caractéristique du système
Comme les courbes d’écoulement ne sont pas des lignes droites de viscosité linéaire constante, le calcul des pertes de charge est très lourd. Dans ce cas, le calcul des pertes est basé sur l’expérience avec des fluides particuliers.