Méthode de division synthétique
Je dois dire que la division synthétique est la façon la plus « amusante » de diviser des polynômes. Elle comporte moins d’étapes pour arriver à la réponse par rapport à la méthode de division longue polynomiale. Dans cette leçon, je vais passer en revue cinq (5) exemples qui devraient, je l’espère, vous familiariser avec les procédures de base pour réussir à diviser des polynômes en utilisant la division synthétique.
Ce qu’il faut retenir:
- S’assurer que le dividende est sous forme standard. Cela signifie que les puissances sont en ordre décroissant.
- Le diviseur doit être sous la forme x – \left( c \right).
Exemples de comment diviser des polynômes en utilisant la division synthétique
Exemple 1 : Divisez le polynôme ci-dessous.
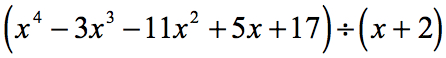
Réexaminons le problème donné et faisons les ajustements nécessaires, si besoin est.
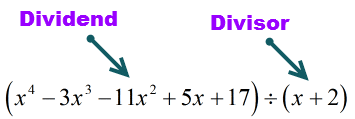
Le dividende (truc à diviser) est sous forme standard car les exposants sont en ordre décroissant. C’est bien !
Le diviseur doit être réécrit sous la forme
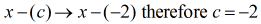
À ce stade, je peux maintenant mettre en place la division synthétique en extrayant les coefficients du dividende puis en les alignant par dessus.
Directement à gauche, placez la valeur de c = – 2 à l’intérieur de la « boîte ».
Enfin, construisez une ligne horizontale juste en dessous des coefficients du dividende.
Étapes:
1. Faites tomber le premier coefficient sous la ligne horizontale.
2. Multipliez ce nombre que vous faites tomber par le nombre dans la « boîte ». Quel que soit son produit, placez-le au-dessus de la ligne horizontale juste en dessous du deuxième coefficient.
3. Additionnez la colonne de nombres, puis placez la somme directement sous la ligne horizontale.
4. Répétez le processus jusqu’à ce que vous n’ayez plus de colonnes à additionner.
Voyez la solution animée ci-dessous:
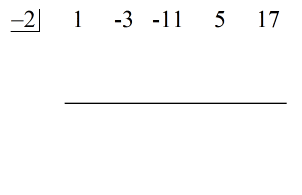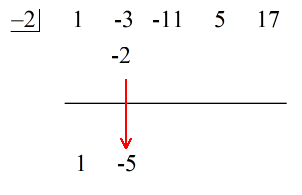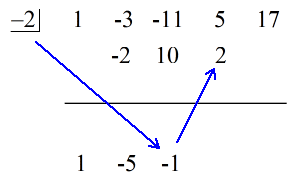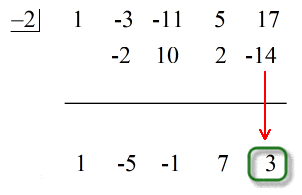
Le dernier nombre sous la ligne horizontale est toujours le reste ! Le reste de ce problème est 3.
Comment présentons-nous donc notre réponse finale ?
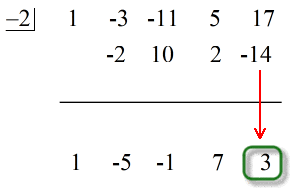
- Présentez votre réponse finale sous la forme
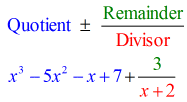
Notez que les nombres sous la ligne horizontale sauf le dernier (reste) sont les coefficients du quotient.
Plus encore, les exposants des variables du quotient sont tous réduits de 1.
Exemple 2 : Divisez le polynôme.
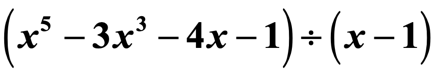
Ce n’est pas une question piège. Remarquez que le quotient ne comporte pas tous les exposants de la variable x.
Je constate qu’il nous manque {x^4} et {x^2}. Pour inclure tous les coefficients de la variable x en puissance décroissante, nous devrions réécrire le problème original comme ceci. Attachez des zéros à ces x manquants. Exprimer également le diviseur comme x – (c) ce qui révèle clairement la valeur de c, c’est-à-dire c = + 1.
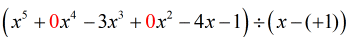
À partir de ce point, je peux maintenant mettre en place les chiffres pour continuer avec le processus.
Étapes:
1. Déposez le premier coefficient sous la ligne horizontale.
2. Multipliez ce nombre que vous déposez par le nombre dans la « boîte ». Quel que soit son produit, placez-le au-dessus de la ligne horizontale juste en dessous du deuxième coefficient.
3. Additionnez la colonne de chiffres, puis placez la somme directement sous la ligne horizontale.
4. Répétez le processus jusqu’à ce que vous n’ayez plus de colonnes à additionner.
Voir la solution animée ci-dessous :
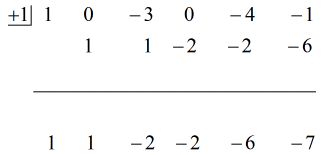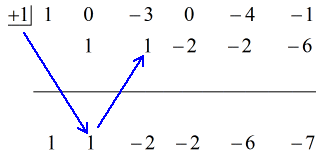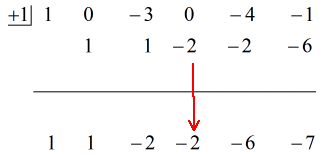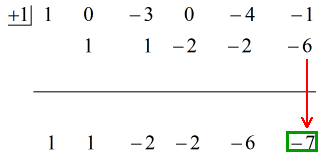
Donc en mettant la réponse finale sous la forme
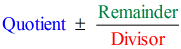
on a
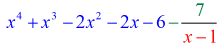
Exemple 3 : Divisez le polynôme ci-dessous.
Gauche( { – 2{x^4} + x} \right) \div \left( {x – 3} \right)
Cela devient plus intéressant ! Le quotient a définitivement l’air horrible car il lui manque beaucoup de choses. Non seulement il manque quelques x qui sont {x^3} et {x^2} mais la constante a également disparu.
Pour corriger cela, je vais réécrire le problème original de telle sorte que tous les x soient pris en compte. Mais plus important encore, n’oubliez pas d’inclure la constante manquante qui est zéro.
Le problème « nouveau et amélioré » devrait ressembler à ceci:
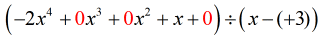
À partir de là, procédez aux étapes comme d’habitude.
Étapes:
1. Déposez le premier coefficient sous la ligne horizontale.
2. Multipliez ce nombre que vous déposez par le nombre dans la « boîte ». Quel que soit son produit, placez-le au-dessus de la ligne horizontale juste en dessous du deuxième coefficient.
3. Additionnez la colonne de chiffres, puis placez la somme directement sous la ligne horizontale.
4. Répétez le processus jusqu’à ce que vous n’ayez plus de colonnes à additionner.
Voir la solution animée ci-dessous:
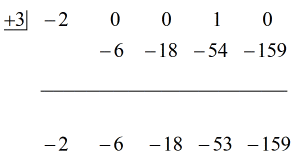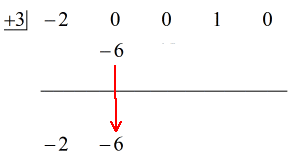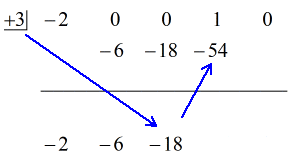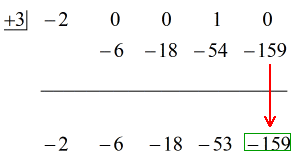
Ok alors, la réponse finale pour ceci est
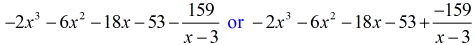
Vous pouvez écrire la réponse finale de deux façons. La première consiste à utiliser le symbole moins ou de soustraction pour indiquer que le reste est négatif. La seconde consiste à utiliser le symbole + mais en attachant un symbole négatif au numérateur. Ils signifient la même chose!
Exemple 4 : Divisez le polynôme ci-dessous.
\left( { – {x^5} + 1} \right) \div \left( {x + 1} \right)
Ne vous laissez pas décourager par ce problème. C’est en fait assez facile, surtout maintenant que vous avez déjà parcouru quelques exemples. N’oubliez jamais de « remplir les parties manquantes », n’est-ce pas ?
Observez le dividende et vous devriez convenir que les parties manquantes sont {x^4}, {x^3}, {x^2} et x.
Réécrire le problème original qui est prêt pour la division synthétique, nous obtenons…
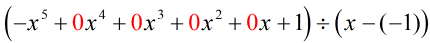
Nous avons peuplé les x manquants avec des zéros et résolu explicitement pour c = -1.
Étapes:
1. Laissez tomber le premier coefficient sous la ligne horizontale.
2. Multipliez ce nombre que vous laissez tomber par le nombre dans la « boîte ». Quel que soit son produit, placez-le au-dessus de la ligne horizontale, juste en dessous du deuxième coefficient.
3. Additionnez la colonne de chiffres, puis placez la somme directement sous la ligne horizontale.
4. Répétez le processus jusqu’à ce que vous n’ayez plus de colonnes à ajouter.
Voyez la solution animée ci-dessous :
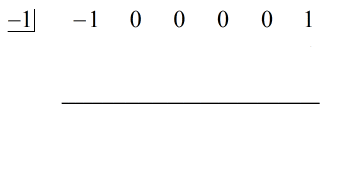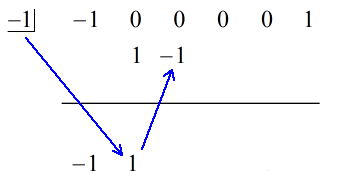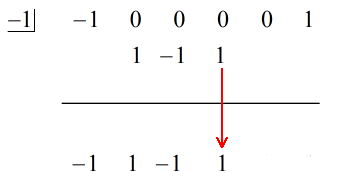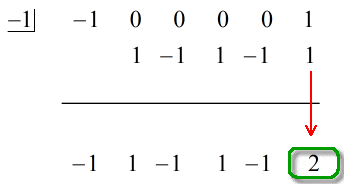
Le dernier nombre sous la ligne horizontale sera toujours le reste. Ne l’oubliez pas. Dans ce cas, le reste est égal à 2.
Notre réponse finale est
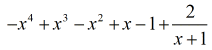
Exemple 5 : Diviser le polynôme par un binôme.
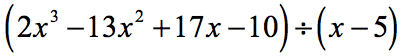
Dans cet exemple, nous obtiendrons un reste égal à zéro. Lorsque cela se produit, le diviseur devient un facteur du dividende. En d’autres termes, le diviseur divise également le dividende.
En examinant le problème, je vois qu’il n’y a pas de composants manquants. Toutes les puissances de x sont prises en compte, et nous avons une constante. C’est génial ! Ce problème est en fait prêt pour la division synthétique.
Étapes:
1. Faites tomber le premier coefficient sous la ligne horizontale.
2. Multipliez ce nombre que vous faites tomber par le nombre dans la « boîte ». Quel que soit son produit, placez-le au-dessus de la ligne horizontale juste en dessous du deuxième coefficient.
3. Additionnez la colonne de chiffres, puis placez la somme directement sous la ligne horizontale.
4. Répétez le processus jusqu’à ce que vous n’ayez plus de colonnes à additionner.
Voir la solution animée ci-dessous :
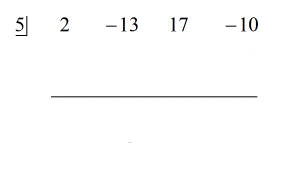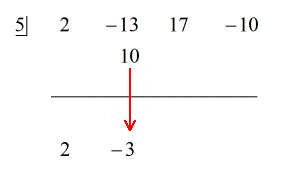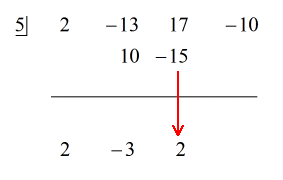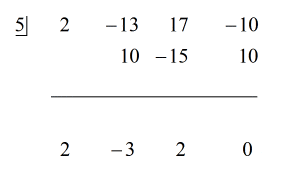
Parce que le reste est égal à zéro, cela signifie que le diviseur x – 5 est un facteur du dividende
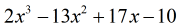
par conséquent
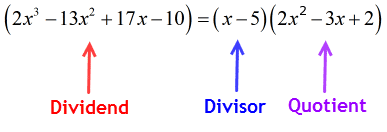
Pratique avec les feuilles de travail
Vous pourriez également être intéressé par :
Addition et soustraction de polynômes
Division de polynômes à l’aide de la méthode de division longue
Multiplication de binômes à l’aide de la méthode FOIL
Multiplication de polynômes
.




