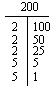Nombres dans leur prime
Tous les nombres entiers sont catégorisés comme étant soit premiers, soit composites, à l’exception de zéro et un, qui sont des cas particuliers. Voyons la différence entre les nombres premiers et les nombres composés. Les nombres premiers ont exactement deux facteurs, un et le nombre lui-même. Si vous connaissez les règles de divisibilité (abordées dans la section suivante), déterminer les nombres premiers de 1 à 100 est une tâche relativement facile. Voici les nombres premiers jusqu’à 25:
2, 3, 5, 7, 11, 13, 17, 19, 23
Il n’y a pas de modèle pour trouver tous les nombres premiers qui existent, bien que les mathématiciens aient trouvé des nombres premiers avec près de huit millions de chiffres. C’est l’un des derniers grands mystères mathématiques pour les mathématiciens.
Les nombres composés ont plus de deux facteurs mais pas un nombre infini de facteurs. Tous les nombres pairs (sauf le nombre deux) sont composites, puisqu’ils peuvent tous être divisés par deux.
Zéro n’est ni premier ni composite. Puisque tout nombre fois zéro est égal à zéro, il y a un nombre infini de facteurs pour un produit de zéro. Un nombre composite doit avoir un nombre fini de facteurs.
Un n’est également ni premier ni composite. La seule façon d’obtenir un produit de un est de multiplier 1 x 1. Mais les facteurs dupliqués ne sont comptés qu’une fois, donc un n’a qu’un seul facteur. (Un nombre premier a exactement deux facteurs, donc un ne peut pas être premier.)
Une question de test typique vous demanderait d’identifier quel nombre d’une liste est premier (ou composite ou ni l’un ni l’autre).
Essayez celle-ci:
Question
Lequel des suivants est un nombre premier ?
- 33
- 45
- 41
- 51
Dévoiler la réponse
La bonne réponse est C. Quarante et un est un nombre premier ; les autres nombres sont composites. Faites attention avec 51 – il vient de 3 x 17.
Règles de divisibilité
Les règles de divisibilité sont des outils pour vous aider à faire moins de divisions. Les règles de divisibilité peuvent vous aider à déterminer si un nombre est premier ou composite ainsi qu’à décomposer les nombres composites en leurs facteurs premiers, sujet que nous aborderons ensuite.
Les règles de divisibilité sont des raccourcis pour vous dire si un nombre est divisible par un autre nombre. Ces règles couvrent la division par les nombres 2 à 10 et vous permettent de vérifier les nombres jusqu’à 100. Cliquez sur les nombres dans le tableau.
| Règles de divisibilité | ||
|---|---|---|
| 2 | 3 | 4 |
| 5 | 6 | 7 |
| 8 | 9 | 10 |
Question
Lequel des nombres suivants n’est pas divisible par 3 ?
- 4 873
- 7 521
- 12 642
- 25 308
Dévoiler la réponse
La bonne réponse est A. La façon rapide de faire ce problème est d’utiliser la règle de divisibilité ; ajouter les chiffres de chaque nombre en cherchant celui qui n’est pas un multiple de trois. La façon lente serait de faire chaque problème de division – même sur une calculatrice, cette méthode prendra plus de temps!
Factorisation de nombres premiers : T et arbre
Voici un autre sujet auquel vous n’avez peut-être pas pensé depuis le collège. Le théorème fondamental de l’arithmétique stipule que chaque nombre composite peut être décomposé en un produit unique de nombres premiers.
La factorisation primaire est le processus qui trouve les produits de nombres premiers d’un nombre composite donné. La factorisation première est utile en soi, mais beaucoup de ses applications impliquent des fractions, que nous couvrirons plus tard.
Vous pouvez peut-être trouver la factorisation première d’un nombre dans votre tête. Par exemple, 12 est 2 x 2 x 3 ou 22 x 3. (Les factorisations premières sont souvent représentées avec des exposants.)
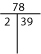
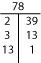
Si vous ne pouvez pas trouver la factorisation première mentalement, essayez soit un Facteur-T ou un Arbre des facteurs.
Revue
- Les nombres premiers ont exactement deux facteurs, un et lui-même.
- Les nombres composés ont plus de deux facteurs mais pas un nombre infini.
- Zéro et un ne sont ni premiers ni composés.
- Les règles de divisibilité sont des raccourcis qui peuvent vous aider à déterminer les facteurs d’un nombre.
- Chaque nombre composite peut être écrit comme un produit unique de nombres premiers, ce qu’on appelle la factorisation première d’un nombre.
- Deux méthodes pratiques pour trouver les factorisations premières sont les facteurs T et les arbres de facteurs.