Propriétés des quadrilatères – Rectangle, carré, parallélogramme, losange, trapèze
En géométrie euclidienne, un quadrilatère est une figure 2D à quatre côtés dont la somme des angles internes est égale à 360°. Le mot quadrilatère est dérivé de deux mots latins « quadri » et « latus » signifiant respectivement quatre et côté. Par conséquent, identifier les propriétés des quadrilatères est important lorsqu’on essaie de les distinguer des autres polygones.
Alors, quelles sont les propriétés des quadrilatères ? Il existe deux propriétés des quadrilatères :
- Un quadrilatère doit être une forme fermée avec 4 côtés
- Tous les angles internes d’un quadrilatère s’additionnent à 360°
Dans cet article, vous aurez une idée des 5 types de quadrilatères et apprendrez à connaître les propriétés des quadrilatères.
Voici ce que vous allez lire dans cet article :
- Différents types de quadrilatères
- Rectangle
- Propriétés des rectangles
- Formules des rectangles
- Place
- Propriétés. d’un carré
- Formules des carrés
- Parallélogramme
- Propriétés des parallélogrammes
- Formules des parallélogrammes
- . Rhombus
- Propriétés d’un rhombus
- Formules du rhombus
- Trapèze/Trapézoïde
- Propriétés d’un trapèze
- Formules du trapèze
.
- Propriétés des quadrilatères
- Formules importantes des quadrilatères
- Questions sur les quadrilatères
Voici une vidéo expliquant les propriétés des quadrilatères :
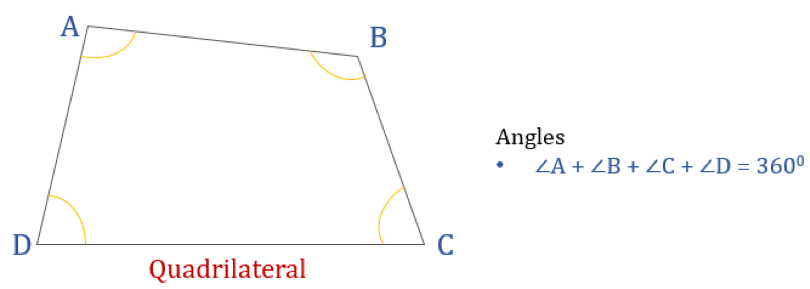
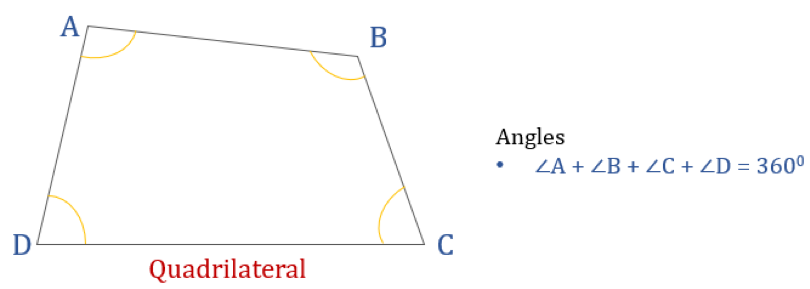
Le schéma donné ci-dessous montre un quadrilatère ABCD et la somme de ses angles internes. La somme de tous les angles internes est de 360°.
Donc, ∠A + ∠B + ∠C + ∠D = 360°
Différents types de quadrilatères
Il existe 5 types de quadrilatères sur la base de leur forme. Ces 5 quadrilatères sont :
- Rectangle
- Square
- Parallélogramme
- Rhombe
- Trapézoïde
Discutons chacun de ces 5 quadrilatères en détail :
Voici des questions qui vous apprendront à appliquer les propriétés des 5 quadrilatères que vous apprendrez dans cet article.
Rectangle
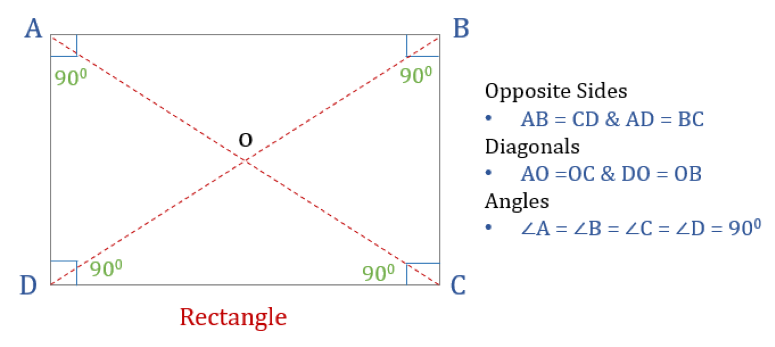
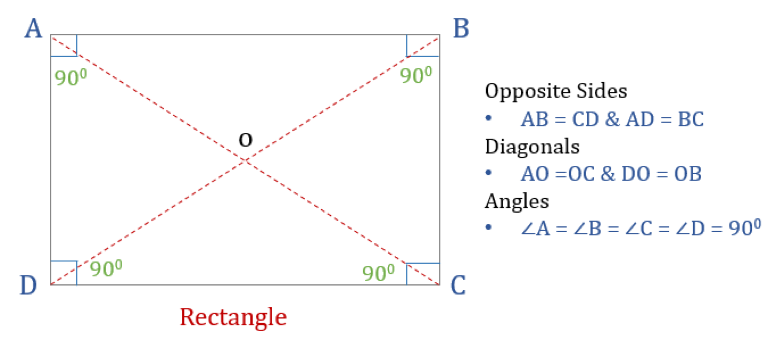
Un rectangle est un quadrilatère avec quatre angles droits. Ainsi, tous les angles d’un rectangle sont égaux (360°/4 = 90°). De plus, les côtés opposés d’un rectangle sont parallèles et égaux, et les diagonales se coupent en deux.
Propriétés des rectangles
Un rectangle a trois propriétés :
- Tous les angles d’un rectangle sont de 90°
- Les côtés opposés d’un rectangle sont égaux et parallèles
- Les diagonales d’un rectangle se coupent en deux
Formule du rectangle – Aire et périmètre d’un rectangle
Si la longueur du rectangle est L et la largeur est B alors,
- Aire d’un rectangle = Longueur × Largeur ou L × B
- Périmètre du rectangle = 2 × (L + B)
Ces questions pratiques vous aideront à solidifier les propriétés des rectangles
Square
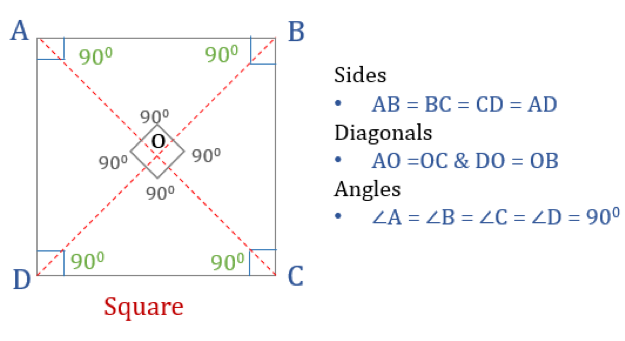
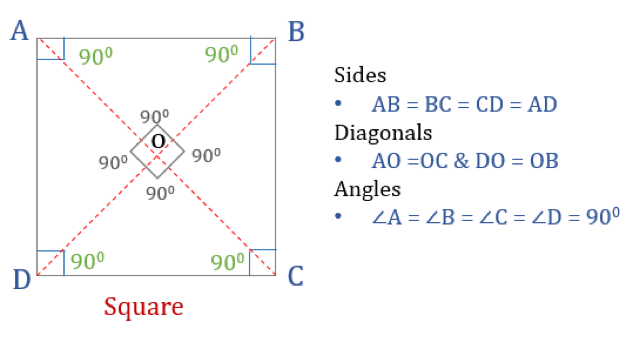
Le carré est un quadrilatère avec quatre côtés et angles égaux. C’est aussi un quadrilatère régulier car ses côtés et ses angles sont égaux. Tout comme un rectangle, un carré a quatre angles de 90° chacun. Il peut aussi être vu comme un rectangle dont les deux côtés adjacents sont égaux.
Propriétés d’un carré
Pour qu’un quadrilatère soit un carré, il doit avoir certaines propriétés. Voici les trois propriétés des carrés :
- Tous les angles d’un carré sont de 90°
- Tous les côtés d’un carré sont égaux et parallèles les uns aux autres
- Les diagonales se coupent en deux perpendiculairement
Formule du carré – Aire et périmètre d’un carré
Si le côté d’un carré est ‘a’ alors,
- Aire du carré = a × a = a²
- Périmètre du carré = 2 × (a + a) = 4a
Ces questions pratiques vous aideront à solidifier les propriétés des carrés
Réussir un Q50-51 au GMAT vous aide à obtenir un score de 700+ au GMAT. Pourquoi ne pas commencer à vous préparer pour le GMAT avec nos ressources de préparation gratuites et commencer votre voyage pour obtenir un Q50-51 au GMAT. Apprenez de Carrie Law qui s’est améliorée de Q35 à Q50 en 3 semaines.
Parallélogramme
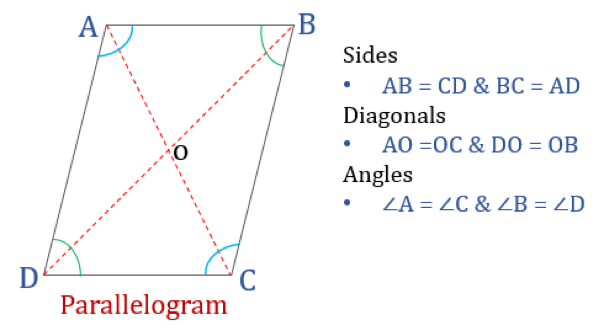
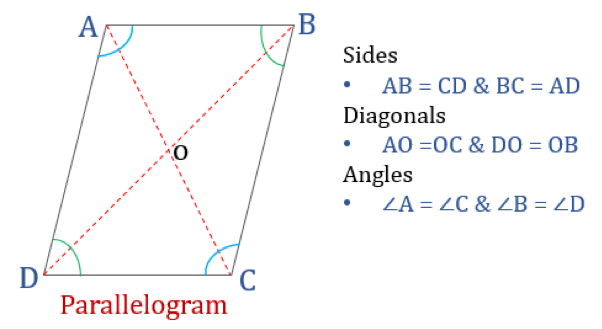
Un parallélogramme, comme son nom l’indique, est un quadrilatère simple dont les côtés opposés sont parallèles. Ainsi, il possède deux paires de côtés parallèles. De plus, les angles opposés dans un parallélogramme sont égaux et ses diagonales se coupent en deux.
Propriétés du parallélogramme
Un quadrilatère satisfaisant aux propriétés mentionnées ci-dessous sera classé comme un parallélogramme. Un parallélogramme possède quatre propriétés :
- Les angles opposés sont égaux
- Les côtés opposés sont égaux et parallèles
- Les diagonales se coupent en deux
- La somme de deux angles adjacents quelconques est de 180°
Formules du parallélogramme – Aire et périmètre d’un parallélogramme
Si la longueur d’un parallélogramme est ‘l’, la largeur est « b » et la hauteur est « h » alors :
- Périmètre du parallélogramme= 2 × (l + b)
- Aire du parallélogramme = l × h
Ces questions d’entraînement vous aideront à consolider les propriétés du parallélogramme
Rhombus
Un rhombus est un quadrilatère dont les quatre côtés sont de longueur égale et les côtés opposés sont parallèles entre eux. Cependant, les angles ne sont pas égaux à 90°. Un rhombe avec des angles droits deviendrait un carré. Un autre nom pour le losange est » diamant » car il ressemble à la couleur diamant dans les cartes à jouer.
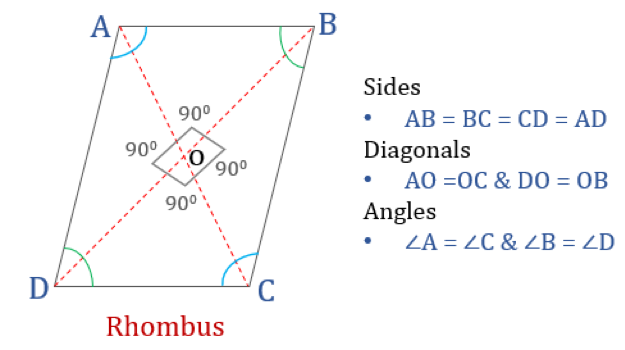
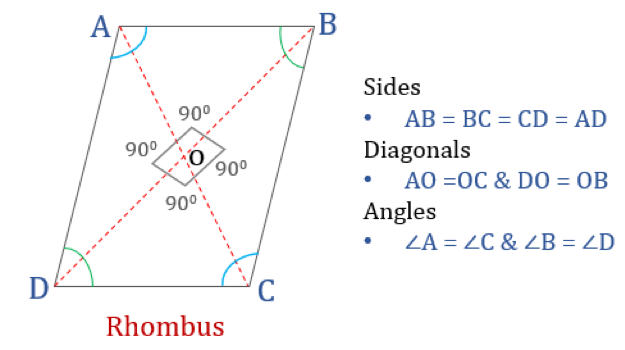
Propriétés du losange
Un losange est un quadrilatère qui possède les quatre propriétés suivantes :
- Les angles opposés sont égaux
- Tous les côtés sont égaux et, les côtés opposés sont parallèles entre eux
- Les diagonales se coupent perpendiculairement
- La somme de deux angles adjacents quelconques est de 180°
Formules du losange – Aire et périmètre d’un losange
Si le côté d’un losange est a alors, le périmètre d’un losange = 4a
Si la longueur de deux diagonales du losange est d1 et d2 alors l’aire d’un losange = ½ × d1 × d2
Ces questions pratiques vont vous aideront à solidifier les propriétés du losange
Trapezium
Un trapèze (appelé Trapezoid aux États-Unis) est un quadrilatère qui n’a qu’une paire de côtés parallèles. Les côtés parallèles sont appelés « bases » et les deux autres côtés sont appelés « pattes » ou côtés latéraux.
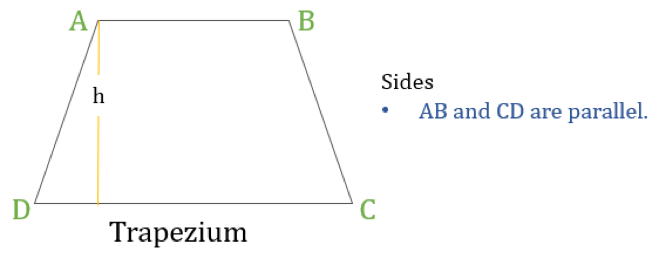
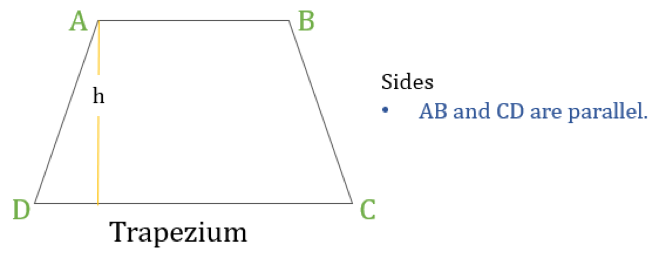
Propriétés du trapèze
Un trapèze est un quadrilatère dont une propriété est la suivante :
- Une seule paire de côtés opposés sont parallèles entre eux
Formules du trapèze – Aire et périmètre d’un trapèze
Si la hauteur d’un trapèze est ‘h’ (comme indiqué dans le diagramme ci-dessus) alors :
- Périmètre du trapèze= Somme des longueurs de tous les côtés = AB + BC + CD + DA
- Aire du trapèze = ½ × (Somme des longueurs des côtés parallèles) × h = ½ × (AB + CD) × h
Ces questions pratiques vous aideront à solidifier les propriétés du trapèze
Propriétés des quadrilatères
Le tableau ci-dessous résume toutes les propriétés des quadrilatères que nous avons appris jusqu’à présent :
| Propriétés des quadrilatères | Rectangle | Square | Parallélogramme | Rhombus | Trapezium | |
| Tous les côtés sont égaux | ✖ | ✔ | ✖ | ✔ | ✖ | |
| Opposés. Les côtés sont égaux | ✔ | ✔ | ✔ | ✔ | ✖ | |
| Opposés Les côtés sont parallèles | ✔ | ✔ | ✔ | ✔ | ✔ | |
| Tous les angles sont égaux | ✔ | ✔ | ✖ | ✖ | ✖ | |
| Les angles opposés sont égaux | ✔ | ✔ | ✔ | ✔ | ✖ | ✖ |
| La somme de deux angles adjacents est de 180 | ✔ | ✔ | ✔ | ✔ | ✖ | |
| Se croisent | ✔ | ✔ | ✔ | ✔ | ✖ | |
| Se croisent perpendiculairement | ✖ | ✔ | ✖ | ✔ | ✖ |
L’image ci-dessous résume également les propriétés des quadrilatères :
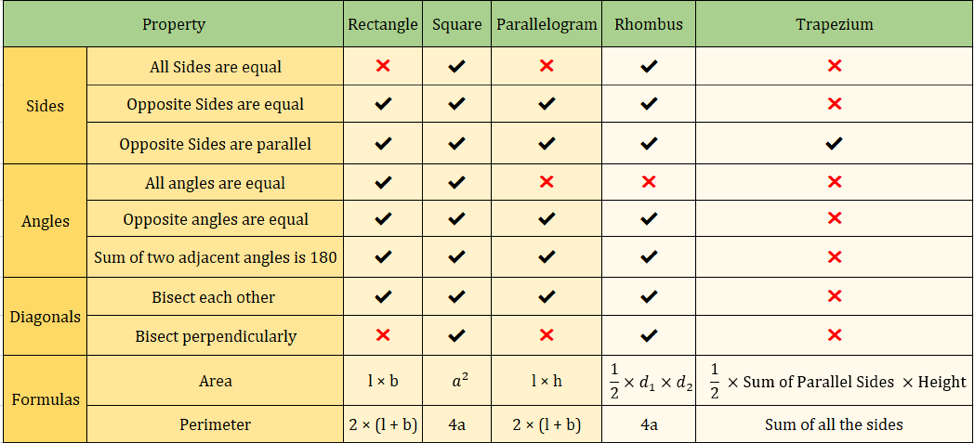
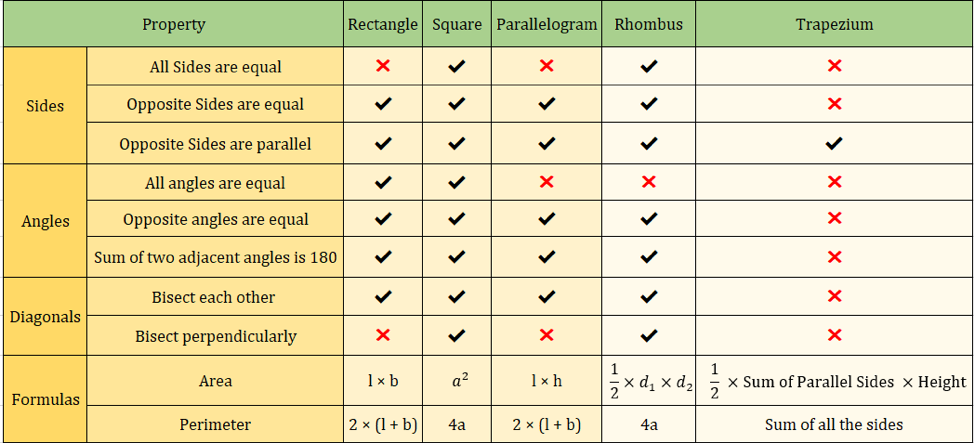
Formules importantes des quadrilatères
Le tableau ci-dessous résume les formules sur l’aire et le périmètre des différents types de quadrilatères :
| Formules des quadrilatères | Rectangle | Square | Parallélogramme | Rhombus | Trapezium |
| Aire | l × b | a² | l × h | ½ × d1 × d2 | ½ × (Somme des côtés parallèles) × hauteur |
| Perimètre | 2 × (l + b) | 4a | 2 × (l + b) | 4a | Somme de tous les côtés |
Lecture complémentaire :
- Propriétés du cercle | Formules du cercle – Aire et périmètre
- Propriétés des nombres – Pair &Ordinaire | Premier | HCF & LCM
- Propriétés des triangles – Définition | Types | Classification
- . Classification
- Lignes et angles – Propriétés et leur application
Questions sur les quadrilatères
Pratiquons l’application des propriétés des quadrilatères sur les exemples de questions suivantes :
Question 1
Adam veut construire une clôture autour de son jardin rectangulaire de longueur 10 mètres et de largeur 15 mètres. Combien de mètres de clôture doit-il acheter pour clôturer tout le jardin ?
- 20 mètres
- 25 mètres
- 30 mètres
- 40 mètres
- 50 mètres
Solution
Étape 1 : Étant donné
- Adam a un jardin rectangulaire.
- Il a une longueur de 10 mètres et une largeur de 15 mètres.
- Il veut construire une clôture autour.
Étape 2 : Trouver
- La longueur nécessaire pour construire la clôture autour du jardin entier.
Etape 3 : Approche et calcul
La clôture ne peut être construite que sur les côtés extérieurs du jardin.
- Donc, la longueur totale de la clôture nécessaire= Somme des longueurs de tous les côtés du jardin.
- Puisque le jardin est rectangulaire, la somme des longueurs de tous les côtés n’est rien d’autre que le périmètre du jardin.
- Périmètre = 2 × (10 + 15) = 50 mètres
Donc, la longueur requise de la clôture est de 50 mètres.
Par conséquent, l’option E est la bonne réponse.
Question : 2
Steve veut peindre un mur de forme rectangulaire de sa chambre. Le coût de la peinture du mur est de 1,5 $ par mètre carré. Si le mur fait 25 mètres de long et 18 mètres de large, alors quel est le coût total pour peindre le mur ?
- $ 300
- $ 350
- $ 450
- $ 600
- $ 675
Solution
Étape 1 : Étant donné
- Steve veut peindre un mur de sa chambre.
- Le mur fait 25 mètres de long et 18 mètres de large.
- Le coût pour peindre le mur est de 1,5 $ par mètre carré.
Etape 2 : Trouver
- Le coût total pour peindre le mur.
Etape 3 : Approche et calcul
- Un mur est peint sur toute sa surface.
- Donc, si on trouve la surface totale du mur en mètres carrés et qu’on la multiplie par le coût pour peindre 1 mètre carré du mur alors on peut le coût total.
- Surface du mur = longueur × largeur = 25 mètres × 18 mètres = 450 mètres carrés
- Coût total pour peindre le mur = 450 × 1.5 $ = 675 $
Donc, la bonne réponse est l’option E.
Nous espérons qu’à ce jour vous auriez appris les différents types de quadrilatères, leurs propriétés et leurs formules et comment appliquer ces concepts pour résoudre des questions sur les quadrilatères. L’application des quadrilatères est importante pour résoudre les questions de géométrie du GMAT. Si vous envisagez de passer le GMAT, nous pouvons vous aider avec du matériel d’étude de haute qualité auquel vous pouvez accéder gratuitement en vous inscrivant ici.
Voici quelques autres articles sur les mathématiques :
- Améliorer la précision des questions de mathématiques sur les polygones
- Questions de géométrie – erreurs les plus courantes | GMAT Quant Prep
Si vous envisagez de passer le GMAT, nous pouvons vous donner accès à un contenu en ligne de qualité pour vous préparer. Nous sommes la société de préparation au GMAT la plus évaluée sur gmatclub avec plus de 1950 avis.
Pourquoi ne pas faire un essai gratuit et juger par vous-même ?
Écrivez-nous à [email protected] en cas de question.




