Skewness – Introduction rapide, exemples et formules
Skewness est un nombre qui indique dans quelle mesure
une variable est distribuée de manière asymétrique.
- Exemple d’asymétrie positive (droite)
- Exemple d’asymétrie négative (gauche)
- Asymétrie de la population – formule et calcul
- Asymétrie de l’échantillon – formule et calcul. Formule et calcul
- Skewness dans SPSS
- Skewness – Implications pour l’analyse des données
Positive (Right) Skewness Exemple
Un scientifique fait passer 1,000 personnes de passer certains tests psychologiques. Pour le test 5, les scores du test ont une asymétrie = 2,0. Un histogramme de ces scores est présenté ci-dessous.
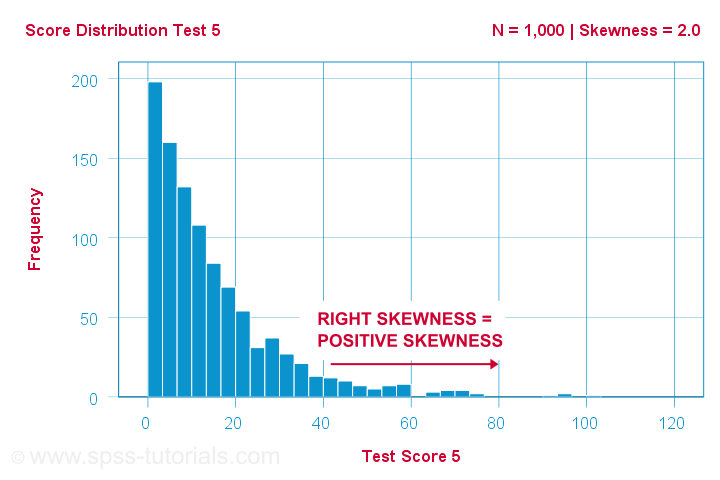
L’histogramme montre une distribution de fréquence très asymétrique. La plupart des personnes obtiennent un score de 20 points ou moins, mais la queue droite s’étend jusqu’à 90 environ. Cette distribution est asymétrique à droite.
Si on se déplace vers la droite le long de l’axe des x, on passe de 0 à 20 à 40 points et ainsi de suite. Donc vers la droite du graphique, les scores deviennent plus positifs. Par conséquent, l’asymétrie droite est une asymétrie positive, ce qui signifie que l’asymétrie > 0. Ce premier exemple a une asymétrie = 2,0 comme indiqué dans le coin supérieur droit du graphique. Les scores sont fortement asymétriques positivement.
Exemple d’asymétrie négative (gauche)
Une autre variable -les scores au test 2- s’avèrent avoir une asymétrie = -1,0. Leur histogramme est présenté ci-dessous.

La majeure partie des scores se situe entre 60 et 100 environ. Cependant, la queue gauche est quelque peu étirée. Cette distribution est donc asymétrique à gauche.
Droite : à gauche, à gauche. Si on suit l’axe des x vers la gauche, on se dirige vers des scores plus négatifs. C’est pourquoi l’asymétrie gauche est une asymétrie négative.Et en effet, l’asymétrie = -1,0 pour ces scores. Leur distribution est asymétrique à gauche. Cependant, elle est moins asymétrique -ou plus symétrique- que notre premier exemple qui avait une asymétrie = 2,0.
La distribution symétrique implique une asymétrie nulle
Enfin, les distributions symétriques ont une asymétrie = 0. Les scores du test 3 -ayant une asymétrie = 0,1- s’en approchent.

Maintenant, les distributions observées sont rarement précisément symétriques. Cela s’observe surtout pour certaines distributions d’échantillonnage théoriques. Quelques exemples sont
- la distribution normale (standard);
- la distribution t et
- la distribution binomiale si p = 0,5.
Ces distributions sont toutes exactement symétriques et ont donc une asymétrie = 0.000…
Assymétrie de la population – Formule et calcul
Si vous souhaitez calculer l’asymétrie d’une ou plusieurs variables, laissez simplement les calculs à un logiciel. Mais -juste pour être complet- je vais quand même énumérer les formules.
Si vos données contiennent toute votre population, calculez l’asymétrie de la population comme :
$Population;skewness = \Sigma\biggl(\frac{X_i – \mu}{\sigma}\biggr)^3\cdot\frac{1}{N}$
où
- \(X_i\) est chaque score individuel ;
- \(\mu\) est la moyenne de la population;
- \(\sigma\) est l’écart type de la population et
- \(N\) est la taille de la population.
Pour un exemple de calcul utilisant cette formule, voir cette feuille Googlesheet (présentée ci-dessous).
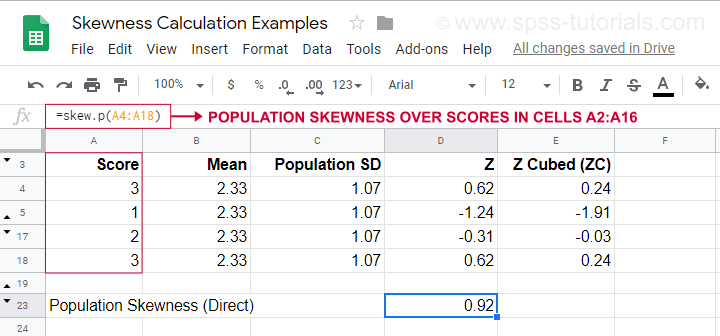
Elle montre également comment obtenir directement l’asymétrie de la population en utilisant=SKEW.P(…)où « .P » signifie « population ». Cela confirme le résultat de notre calcul manuel. Malheureusement, ni SPSS ni JASP ne calculent l’asymétrie de population : tous deux sont limités à l’asymétrie d’échantillon.
S skewness d’échantillon – Formule et calcul
Si vos données détiennent un simple échantillon aléatoire d’une certaine population, utilisez
$$Sample\ ;skewness = \frac{N\cdot\Sigma(X_i – \overline{X})^3}{S^3(N – 1)(N – 2)}$$
où
- \(X_i\) est chaque score individuel ;
- \(\overline{X}\) est la moyenne de l’échantillon;
- \(S\) est l’écart-type de l’échantillon et
- \(N\) est la taille de l’échantillon.
Un exemple de calcul est présenté dans ce Googlesheet (présenté ci-dessous).
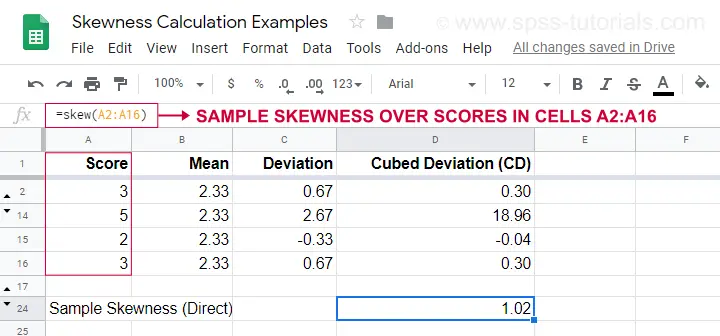
Une option plus facile pour obtenir l’asymétrie de l’échantillon est d’utiliser=SKEW(…).ce qui confirme le résultat de notre calcul manuel.
L’asymétrie dans SPSS
Tout d’abord, « l’asymétrie » dans SPSS fait toujours référence à l’asymétrie d’échantillon : elle suppose tranquillement que vos données contiennent un échantillon plutôt qu’une population entière. Il y a beaucoup d’options pour l’obtenir. Ma préférée est MEANS, car la syntaxe et la sortie sont claires et simples. Les captures d’écran ci-dessous vous guident.

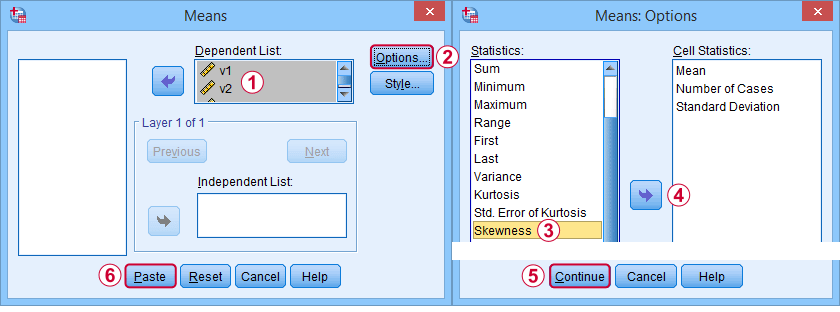
La syntaxe peut être aussi simple quemeans v1 to v5
/cells skew.Un tableau très complet -comprenant les moyennes, les écarts types, les médianes et plus encore- est exécuté à partir demeans v1 to v5
/cells count min max mean median stddev skew kurt.Le résultat est présenté ci-dessous.
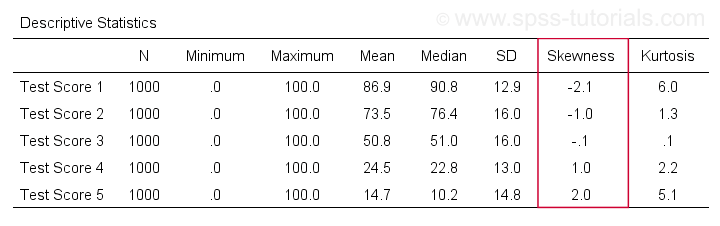
Ascarte – Implications pour l’analyse des données
De nombreuses analyses -ANOVA, tests t, régression et autres – nécessitent l’hypothèse de normalité : les variables doivent être normalement distribuées dans la population. La distribution normale a une asymétrie = 0. Donc, l’observation d’une asymétrie substantielle dans certaines données d’échantillon suggère que l’hypothèse de normalité est violée.
Ces violations de la normalité ne posent pas de problème pour les grandes tailles d’échantillon -selon N > 20 ou 25 environ. Dans ce cas, la plupart des tests sont robustes à de telles violations. Ceci est dû au théorème de la limite centrale. En bref, pour les échantillons de grande taille, l’asymétrie n’est
pas un réel problème pour les tests statistiques.Cependant, l’asymétrie est souvent associée à de grands écarts types. Cependant, l’asymétrie est souvent associée à des écarts types importants, ce qui peut entraîner des erreurs types importantes et une faible puissance statistique. Ainsi, une asymétrie importante peut diminuer les chances de rejeter une hypothèse nulle afin de démontrer un effet. Dans ce cas, un test non paramétrique peut être un choix plus judicieux car il peut avoir plus de puissance.les violations de la normalité posent une réelle menace
pour les petites tailles d’échantillon de -disons- N < 20 ou plus. Avec de petites tailles d’échantillon, de nombreux tests ne sont pas robustes contre une violation de l’hypothèse de normalité. La solution -encore une fois- est d’utiliser un test non paramétrique car ceux-ci ne requièrent pas la normalité.
Enfin, il n’y a pas de test statistique pour examiner si l’asymétrie de la population = 0. Une façon indirecte de tester cela est un test de normalité tel que
- le test de normalité de Kolmogorov-Smirnov et
- le test de normalité de Shapiro-Wilk.
Cependant, lorsque la normalité est vraiment nécessaire -avec des échantillons de petite taille- ces tests ont une faible puissance : ils peuvent ne pas atteindre la signification statistique même lorsque les écarts à la normalité sont sévères. Ainsi, ils vous procurent principalement un faux sentiment de sécurité.




