Surface d’un cylindre – Explication et exemples
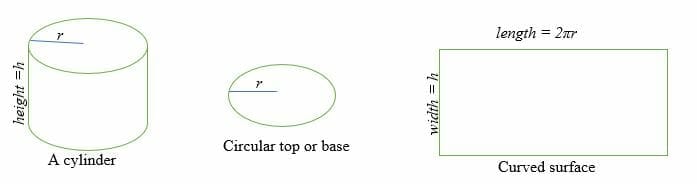
Avant de sauter dans le sujet de la surface d’un cylindre, passons en revue un cylindre. En géométrie, un cylindre est une figure tridimensionnelle avec deux bases circulaires parallèles l’une à l’autre et une surface courbe.
Comment trouver la surface d’un cylindre?
La surface d’un cylindre est la somme de deux faces circulaires parallèles et congruentes et de la surface courbe.
Cet article traitera de la façon de trouver la surface totale et la surface latérale d’un cylindre.
Pour calculer la surface d’un cylindre, vous devez trouver la surface de base (B) et la surface courbe (CSA). Ainsi, l’aire de surface ou la surface totale d’un cylindre est égale à la somme de l’aire de base multipliée par deux et de l’aire de la surface courbe.
La surface courbe d’un cylindre est égale à un rectangle dont la longueur est 2πr et la largeur est h.
Où r = rayon de la face circulaire et h = hauteur du cylindre.
L’aire de la surface courbe = Aire d’un rectangle =l x w = πdh
L’aire de base, B = Aire d’un cercle = πr2
La formule de l’aire d’un cylindre
La formule de l’aire totale d’un cylindre est donnée par :
Surface totale d’un cylindre = 2πr2 + 2πrh
TSA = 2πr2 + 2πrh
Où 2πr2 est la surface des faces circulaires supérieure et inférieure, et 2πrh est la surface de la surface courbe.
En prenant 2πr comme facteur commun de RHS, on obtient;
TSA = 2πr (h + r) ……………………………………. (Formule de la surface d’un cylindre)
Résolvons des problèmes d’exemple impliquant la surface d’un cylindre.
Exemple 1
Trouver la surface totale d’un cylindre dont le rayon est de 5 cm et la hauteur de 7 cm.
Solution
Selon la formule,
TSA = 2πr (h + r)
= 2 x 3.14 x 5(7 + 5)
= 31,4 x 12
= 376,8 cm2
Exemple 2
Déterminez le rayon d’un cylindre dont la surface totale est de 2136,56 pieds carrés, et la hauteur est de 3 pieds.
Solution
Donné:
TSA = 2136.56 pieds carrés
Hauteur, h = 3 pieds
Mais, TSA = 2πr (h + r)
2136,56 =2 x 3,14 x r (3 + r)
2136,56 = 6.28r (3 + r)
Par la propriété distributive de la multiplication sur le RHS, nous avons,
2136.56 = 18.84r + 6.28r2
Diviser chaque terme par 6.28
340.22 = 3r + r2
r2 + 3r – 340,22 = 0 ……… (une équation quadratique)
En résolvant l’équation à l’aide de la formule quadratique, on obtient,
r = 17
Donc, le rayon du cylindre est de 17 pieds.
Exemple 3
Le coût de la peinture d’un récipient cylindrique est de 0,04 $ par cm2. Trouvez le coût de la peinture de 20 récipients de rayon, 50 cm, et de hauteur, 80 cm.
Solution
Calculez la surface totale de 20 récipients.
TSA = 2πr (h + r)
= 2 x 3.14 x 50 (80 + 50)
= 314 x 130
= 40820 cm2
La surface totale de 20 conteneurs = 40 820 cm2 x 20
=816 400 cm2
Le coût de la peinture = 816 400 cm2 x 0,04 $.04 $ par cm2
= 32 656 $.
Donc, le coût de la peinture de 20 conteneurs est de 32 656 $.
Exemple 4
Trouve la hauteur d’un cylindre si sa surface totale est de 2552 po2 et son rayon de 14 po.
Solution
Donné :
TSA = 2552 in2
Radius, r = 14 in.
Mais, TSA = 2πr (h + r)
2552 = 2 x 3.14 x 14 (14 + h)
2552 = 87,92(14 + h)
Diviser les deux côtés par 87,92 pour obtenir,
29.026 = 14 + h
Soustraire par 14 des deux côtés.
h = 15
Donc, la hauteur du cylindre est de 15 po.
Surface latérale d’un cylindre
Comme indiqué précédemment, l’aire de la surface incurvée d’un cylindre est ce qu’on appelle la surface latérale. En termes simples, la surface latérale d’un cylindre est la surface d’un cylindre, à l’exclusion de la surface de la base et du fond (surface circulaire).
La formule donne la surface latérale d’un cylindre;
LSA = 2πrh
Exemple 5
Trouvez la surface latérale d’un cylindre dont le diamètre est de 56 cm et la hauteur de 20 cm.
Solution
Donnée:
Diamètre = 56 cm, donc rayon, r =56/2 = 28 cm
Hauteur, h = 20 cm
Par, la formule,
LSA = 2πrh
= 2 x 3.14 x 28 x 20
= 3516,8 cm2.
Donc, la surface latérale du cylindre est de 3516,8 cm2.
Exemple 6
La surface latérale d’un cylindre est de 144 pi2. Si le rayon du cylindre est de 7 ft, trouvez la hauteur du cylindre.
Solution
Donné;
Surface latérale = 144 ft2
Radius, r = 7 ft
.




