A henger felülete – magyarázat és példák
Mielőtt belevágnánk a henger felületének témájába, tekintsük át a hengert. A geometriában a henger egy olyan háromdimenziós alakzat, amelynek két egymással párhuzamos köralapja és görbe felülete van.
Hogyan határozzuk meg egy henger felületét?
A henger felülete a két párhuzamos és kongruens köralap és a görbe felület összege.
Ez a cikk azt tárgyalja, hogyan találjuk meg egy henger teljes felületét és oldalfelületét.
A henger felületének kiszámításához meg kell találnunk az alapterületet (B) és az ívelt felületet (CSA). Ezért a henger felülete vagy teljes felülete egyenlő az alapterület kétszeresének és az ívelt felület területének összegével.
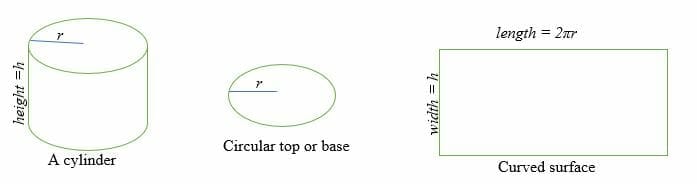
A henger ívelt felülete egyenlő egy téglalapnak, amelynek hossza 2πr és szélessége h.
Hol r = a kör alakú felület sugara és h = a henger magassága.
A görbült felület területe = Egy téglalap területe =l x w = πdh
Az alapterület, B = Egy kör területe = πr2
A henger területének képlete
A henger teljes felületének képlete a következő:
A henger teljes felülete = 2πr2 + 2πrh
TSA = 2πr2 + 2πrh
Ahol 2πr2 a felső és alsó körfelület területe, 2πrh pedig az ívelt felület területe.
Az RHS-ből a 2πr-t közös tényezőnek véve, megkapjuk;
TSA = 2πr (h + r) ……………………………………. ……………………………………. (Egy henger felületének képlete)
Megoldjuk a henger felületével kapcsolatos példafeladatokat.
1. példa
Keresd meg egy olyan henger teljes felületét, amelynek sugara 5 cm és magassága 7 cm.
Megoldás
A képlet szerint,
TSA = 2πr (h + r)
= 2 x 3.14 x 5(7 + 5)
= 31,4 x 12
= 376,8 cm2
2. példa
Meghatározzuk egy olyan henger sugarát, amelynek teljes felülete 2136,56 négyzetláb, magassága pedig 3 láb.
Megoldás
Adott:
TSA = 2136.56 négyzetláb
Magasság, h = 3 láb
De, TSA = 2πr (h + r)
2136,56 =2 x 3,14 x r (3 + r)
2136,56 = 6.28r (3 + r)
A szorzás disztributív tulajdonsága alapján az RHS-en van,
2136,56 = 18,84r + 6,28r2
Elosztjuk az egyes tagokat 6,28-al
340.22 = 3r + r2
r2 + 3r – 340,22 = 0 ……… (négyzetes egyenlet)
Az egyenletet a négyzetes képlet segítségével megoldva azt kapjuk,
r = 17
Ezért a henger sugara 17 láb.
3. példa
Egy hengeres tartály festésének költsége 0,04 dollár/cm2. Határozzuk meg 20 db 50 cm sugarú és 80 cm magas tartály festésének költségét.
Megoldás
Kalkuláljuk ki a 20 tartály teljes felületét.
TSA = 2πr (h + r)
= 2 x 3.14 x 50 (80 + 50)
= 314 x 130
= 40820 cm2
A 20 konténer teljes felülete = 40 820 cm2 x 20
=816 400 cm2
A festés költsége = 816 400 cm2 x 0 $.04 per cm2
= $32,656.
Az 20 konténer festésének költsége tehát $32,656.
4. példa
Következtessük egy henger magasságát, ha a teljes felülete 2552 in2 és a sugara 14 in.
megoldás
Adva:
TSA = 2552 in2
Sugár, r = 14 in.
De, TSA = 2πr (h + r)
2552 = 2 x 3.14 x 14 (14 + h)
2552 = 87,92(14 + h)
Elosztjuk mindkét oldalt 87,92-vel, hogy megkapjuk,
29.026 = 14 + h
Mindkét oldalon vonjuk ki 14-gyel.
h = 15
Ezért a henger magassága 15 in.
A henger oldalfelülete
Mint már említettük, a henger ívelt felületének területét oldalfelületnek nevezzük. Egyszerűen fogalmazva, a henger oldalfelülete a henger felülete, kivéve az alap és az alj területét (körfelület).
A képlet megadja a henger oldalfelületét;
LSA = 2πrh
5. példa
Következtessük egy olyan henger oldalfelületét, amelynek átmérője 56 cm és magassága 20 cm.
megoldás
Adva:
átmérő = 56 cm, tehát sugár, r =56/2 = 28 cm
magasság, h = 20 cm
A képlet szerint,
LSA = 2πrh
= 2 x 3.14 x 28 x 20
= 3516,8 cm2.
Így a henger oldalfelülete 3516,8 cm2.
6. példa
A henger oldalfelülete 144 ft2. Ha a henger sugara 7 ft, határozzuk meg a henger magasságát.
Megoldás
Megadva;
LSA = 144 ft2
Sugár, r = 7 ft
Sugár, r = 7 ft




