A lineáris regresszió együtthatóinak értelmezése

A lineáris regresszió együtthatóinak értelmezése

Ma már rengeteg gépi tanulási algoritmus létezik, amelyeket kipróbálhatunk, hogy megtaláljuk az adott problémánknak legmegfelelőbbet. Az algoritmusok egy része egyértelmű értelmezéssel rendelkezik, mások blackboxként működnek, és olyan megközelítéseket használhatunk, mint a LIME vagy a SHAP, hogy levezessünk néhány értelmezést.

Ebben a cikkben a legalapvetőbb regressziós modell, nevezetesen a lineáris regresszió együtthatóinak értelmezésére szeretnék koncentrálni, beleértve azokat a helyzeteket is, amikor a függő/független változókat transzformáltuk (jelen esetben log-transzformációról beszélek).

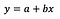
Feltételezem, hogy az olvasó ismeri a lineáris regressziót (ha nem, akkor rengeteg jó cikk és Medium bejegyzés van), ezért kizárólag az együtthatók értelmezésére fogok koncentrálni.

A lineáris regresszió alapképlete fentebb látható (a reziduumokat szándékosan kihagytam, hogy egyszerű és lényegre törő legyen a dolog). A képletben y a függő változót, x pedig a független változót jelöli. Az egyszerűség kedvéért tegyük fel, hogy egyváltozós regresszióról van szó, de az elvek nyilvánvalóan érvényesek a többváltozós esetre is.

Azért, hogy szemléletessé tegyük, mondjuk, hogy a modell illesztése után a következőket kapjuk:

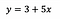
Intercept (a)

Az intercept értelmezését két esetre bontom:

• x folytonos és központosított (ha minden megfigyelésből kivonjuk az x átlagát, akkor a transzformált x átlaga 0 lesz) – az y átlaga 3, ha x egyenlő a minta átlagával
• x folytonos, de nem központosított – y átlaga 3, ha x = 0
• x kategorikus – y átlaga 3, ha x = 0 (ezúttal kategóriát jelez, erről bővebben alább)

Koefficiens (b)

• x folytonos változó

Interpretáció: Az x egységnyi növekedése az átlagos y 5 egységnyi növekedését eredményezi, minden más változót változatlanul hagyva.

• x kategorikus változó

Ez egy kicsit több magyarázatot igényel. Tegyük fel, hogy x a nemet írja le, és vehet fel értékeket (“férfi”, “nő”). Most alakítsuk át dummy-változóvá, amely férfiak esetében 0, nők esetében 1 értéket vesz fel.

Interpretáció: Az átlagos y 5 egységgel magasabb a nők esetében, mint a férfiak esetében, minden más változót változatlanul hagyva.

log-szintű modell

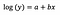
Tipikusan log-transzformációt használunk, hogy a pozitívan ferde eloszlású, kiugró adatokat közelebb hozzuk az adatok nagy részéhez, hogy a változó normális eloszlású legyen. Lineáris regresszió esetén a log-transzformáció használatának egyik további előnye az értelmezhetőség.

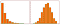
Mint korábban, mondjuk, hogy az alábbi képlet az illesztett modell együtthatóit mutatja be.

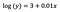
Intercept (a)

Az értelmezés hasonló, mint a vanília (szintszintű) esetben, azonban az értelmezéshez exp(3) = 20,09, az intercept exponensét kell vennünk. A különbség az, hogy ez az érték az y geometriai középértékét jelenti (szemben a számtani középértékkel a szintszintű modell esetében).

Koefficiens (b)

Az elvek ismét hasonlóak a szintszintű modellhez, amikor a kategorikus/numerikus változók értelmezéséről van szó. Az intercepthez hasonlóan az együttható exponensét kell vennünk: exp(b) = exp(0,01) = 1,01. Ez azt jelenti, hogy az x egységnyi növekedése 1%-os növekedést okoz az átlagos (geometriai) y-ban, minden más változót változatlanul hagyva.

Két dolgot érdemes itt megemlíteni:

• Van egy ökölszabály, amikor egy ilyen modell együtthatóinak értelmezéséről van szó. Ha abs(b) < 0,15, akkor egészen biztos, hogy b = 0,1 esetén az x egységnyi változására az y 10%-os növekedését fogjuk megfigyelni. A nagyobb abszolút értékű együtthatók esetében ajánlatos az exponens kiszámítása.
• Ha tartományban lévő változókkal (például százalékos értékkel) van dolgunk, akkor az értelmezés szempontjából kényelmesebb, ha először megszorozzuk a változót 100-zal, és utána illesztjük a modellt. Így az értelmezés intuitívabb, hiszen 100 százalékpont helyett 1 százalékponttal növeljük a változót (0-ról azonnal 1-re).

level-log modell

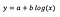
Tegyük fel, hogy a modell illesztése után megkapjuk:

A metszéspont értelmezése ugyanaz, mint a szintszintű modell esetében.

A b együttható esetében – az x 1%-os növekedése az átlagos y közelítőleg b/100 (ebben az esetben 0,05) növekedését eredményezi, minden más változót változatlanul tartva. A pontos összeg megállapításához b× log(1,01) értéket kellene vennünk, ami ebben az esetben 0,0498-at ad.

log-log modell

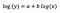
Tegyük fel, hogy a modell illesztése után megkapjuk:

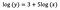
Még egyszer a b értelmezésére koncentrálok. Az x 1%-os növekedése az átlagos (geometriai) y 5%-os növekedését eredményezi, minden más változót változatlanul hagyva. Ahhoz, hogy a pontos összeget megkapjuk,

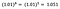
mely ~5,1%.

Következtetések

Remélem, ez a cikk áttekintést adott arról, hogyan kell értelmezni a lineáris regresszió együtthatóit, beleértve azokat az eseteket is, amikor néhány változót log-transzformáltunk. Mint mindig, minden építő jellegű visszajelzést szívesen fogadunk. Elérhet engem a Twitteren vagy a hozzászólásokban.