A négyszögek tulajdonságai – Téglalap, négyzet, párhuzamos, rombusz, trapéz
A négyszög az euklideszi geometriában olyan négyoldalú 2D-s alakzat, amelynek belső szögeinek összege 360°. A négyszögletű szó két latin szóból származik: “quadri” és “latus”, amelyek jelentése négy, illetve oldal. Ezért a négyszögek tulajdonságainak azonosítása fontos, amikor megpróbáljuk megkülönböztetni őket más sokszögektől.
Melyek tehát a négyszögek tulajdonságai? A négyszögeknek két tulajdonsága van:
- A négyszögnek zárt alakzatnak kell lennie 4 oldallal
- A négyszög összes belső szöge 360°-ot tesz ki
Ebben a cikkben képet kapsz a négyszögek 5 típusáról, és megismerheted a négyszögek tulajdonságait.
Ezt fogod olvasni a cikkben:
- A négyszögek különböző típusai
- Négyszög
- A négyszögek tulajdonságai
- A négyszög képletei
- Négyzet
- Tulajdonságai. a négyzet
- A négyzetek képletei
- Paralelogramma
- A párhuzamosok tulajdonságai
- Paralelogramma képletei
- Rombusz
- A rombusz tulajdonságai
- Rombusz képletek
- Trapéz/Trapéz
- A trapéz tulajdonságai
- Trapéz képletek
- Négyszögek tulajdonságai
- Fontos négyszögképletek
- Négyszögek kérdései
Itt egy videó, ami a négyszögek tulajdonságait magyarázza el:
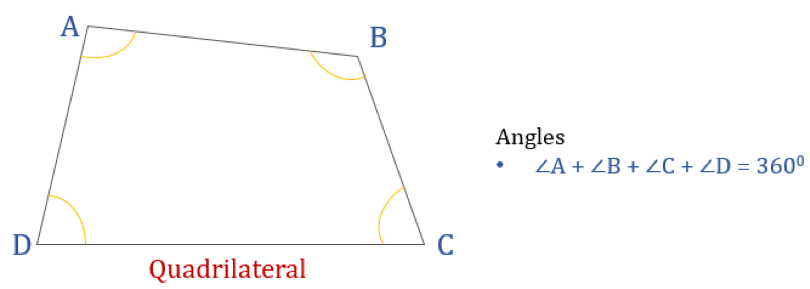
Az alábbi ábrán egy ABCD négyszög és belső szögeinek összege látható. A belső szögek összege 360°.
Így: ∠A + ∠B + ∠C + ∠D = 360°
A négyszögek különböző típusai
A négyszögeknek alakjuk alapján 5 típusa van. Ez az 5 négyszög:
- Téglalap
- Négyzet
- Parallelogramma
- Rombusz
- Trapézium
Ezzel az 5 négyszöggel foglalkozzunk részletesen:
Itt vannak kérdések, amelyekből megtanulhatod, hogyan kell alkalmazni mind az 5 négyszög tulajdonságait, amelyeket ebben a cikkben megtanulsz.
Téglalap
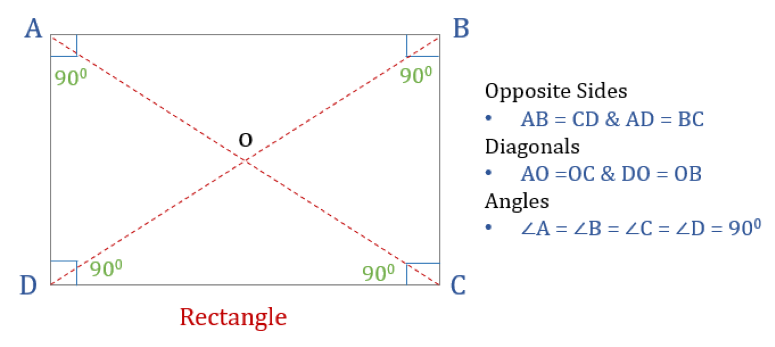
A téglalap olyan négyszög, amelynek négy derékszöge van. Így a téglalap minden szöge egyenlő (360°/4 = 90°). Továbbá a téglalap ellentétes oldalai párhuzamosak és egyenlőek, az átlósok pedig felezik egymást.
A téglalapok tulajdonságai
A téglalapnak három tulajdonsága van:
- A téglalap minden szöge 90°
- A téglalap szemközti oldalai egyenlőek és párhuzamosak
- A téglalap átlói felezik egymást
Téglalap képlete – A téglalap területe és kerülete
Ha a téglalap hossza L és szélessége B akkor,
- Téglalap területe = Hossz × szélesség vagy L × B
- Téglalap kerülete = 2 × (L + B)
Ezek a gyakorló kérdések segítenek megszilárdítani a téglalapok tulajdonságait
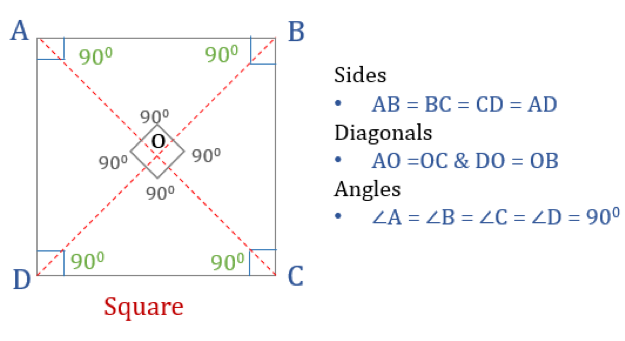
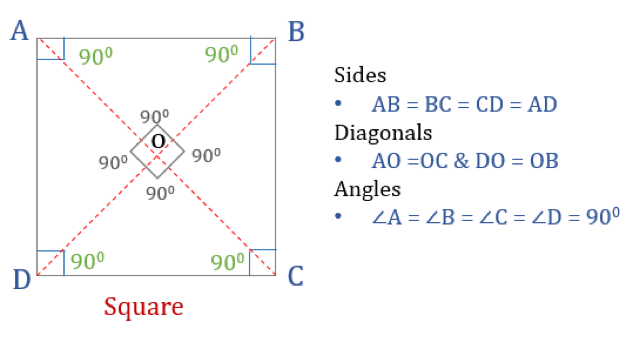
Négyzet
A négyzet egy négyszög négy egyenlő oldallal és szöggel. Ez is egy szabályos négyszög, mivel mind az oldalai, mind a szögei egyenlőek. A téglalaphoz hasonlóan a négyzetnek is négy, egyenként 90°-os szöge van. Úgy is felfogható, mint egy téglalap, amelynek két szomszédos oldala egyenlő.
A négyzet tulajdonságai
Hogy egy négyszög négyzet legyen, bizonyos tulajdonságokkal kell rendelkeznie. Íme a négyzet három tulajdonsága:
- A négyzet minden szöge 90°
- A négyzet minden oldala egyenlő és párhuzamos egymással
- Az átlói merőlegesen felezik egymást
Négyzet képlete – A négyzet területe és kerülete
Ha egy négyzet oldala ‘a’, akkor,
- A négyzet területe = a × a = a²
- A négyzet kerülete = 2 × (a + a) = 4a
Ezek a gyakorló kérdések segítenek megszilárdítani a négyzetek tulajdonságait
A GMAT-on a Q50-51 pontszám elérése segít a 700 feletti GMAT pontszám elérésében. Miért nem kezded el a GMAT-ra való felkészülést ingyenes felkészítő forrásainkkal, és indulj el azon az úton, hogy Q50-51-es eredményt érj el a GMAT-on. Tanulj Carrie Law-tól, aki 3 hét alatt Q35-ről Q50-re javított.
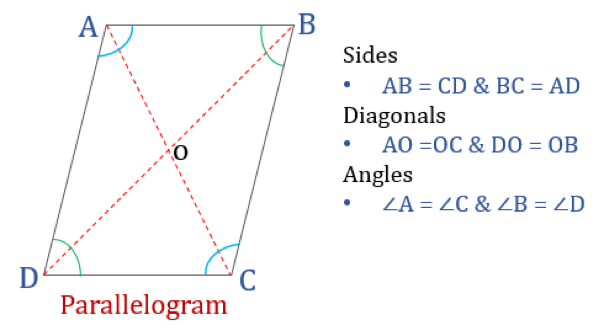
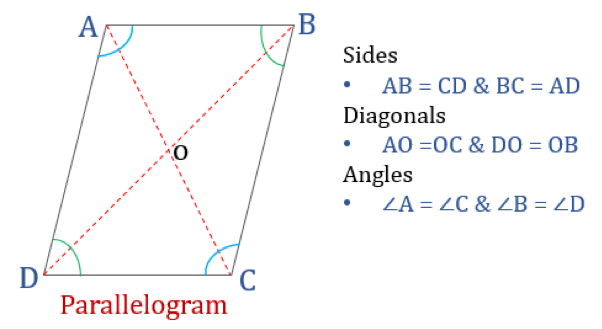
Parallelogramma
A parallelogramma, ahogy a neve is mutatja, egy egyszerű négyszög, amelynek ellentétes oldalai párhuzamosak. Tehát két párhuzamos oldalpárral rendelkezik. Ráadásul a párhuzamosban az ellentétes szögek egyenlőek, és az átlói felezik egymást.
A párhuzamos tulajdonságai
Az alább felsorolt tulajdonságoknak megfelelő négyszöget párhuzamosnak minősítjük. A paralelogramma négy tulajdonsággal rendelkezik:
- A szemben lévő szögek egyenlőek
- A szemben lévő oldalak egyenlőek és párhuzamosak
- Az átlósok felezik egymást
- Minden két szomszédos szög összege 180°
Párhuzamos képletek – A párhuzamos területe és kerülete
Ha a párhuzamos hossza ‘l’, a szélessége ‘b’ és a magassága ‘h’, akkor:
- A paralelogramma kerülete= 2 × (l + b)
- A paralelogramma területe = l × h
Ezek a gyakorló kérdések segítenek megszilárdítani. a párhuzamosok tulajdonságait
Rombusz
A rombusz olyan négyszög, amelynek mind a négy oldala egyenlő hosszúságú, és a szemben lévő oldalak párhuzamosak egymással. A szögek azonban nem egyenlőek 90°-kal. Egy derékszögű rombuszból négyzet lenne. A rombusz másik neve a “rombusz”, mivel hasonlít a játékkártyák rombusz színéhez.
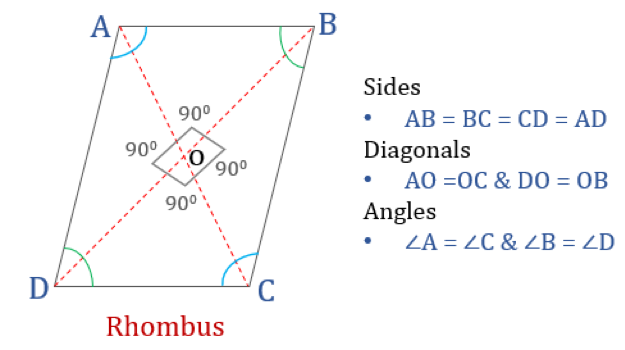
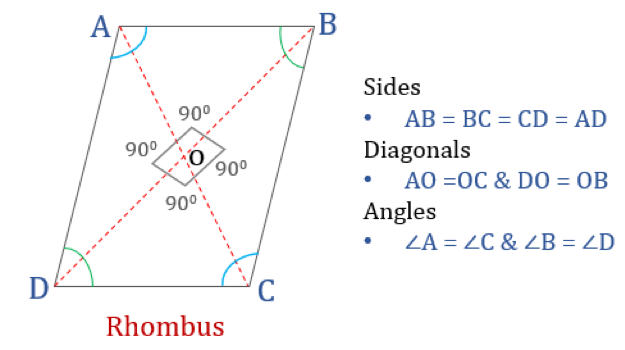
A rombusz tulajdonságai
A rombusz olyan négyszög, amely a következő négy tulajdonsággal rendelkezik:
- Az ellentétes szögek egyenlőek
- Minden oldal egyenlő és, az ellentétes oldalak párhuzamosak egymással
- Az átlósok merőlegesen felezik egymást
- Minden két szomszédos szög összege 180°
Rombusz képletek – A rombusz területe és kerülete
Ha egy rombusz oldala a, akkor, egy rombusz kerülete = 4a
Ha a rombusz két átlójának hossza d1 és d2, akkor a rombusz területe = ½ × d1 × d2
Ezekkel a gyakorló kérdésekkel segítenek megszilárdítani a rombusz tulajdonságait
Trapéz
A trapéz (az USA-ban trapezoidnak nevezik) olyan négyszög, amelynek csak egy pár párhuzamos oldala van. A párhuzamos oldalakat “alapoknak”, a másik két oldalt pedig “lábaknak” vagy oldaloldalaknak nevezzük.
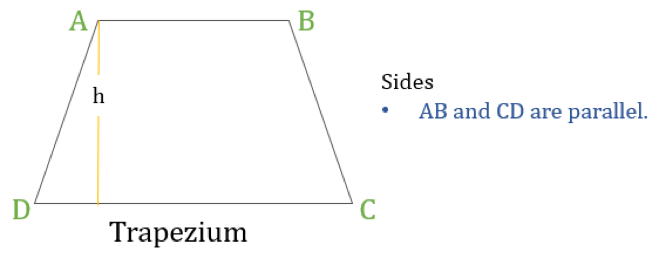
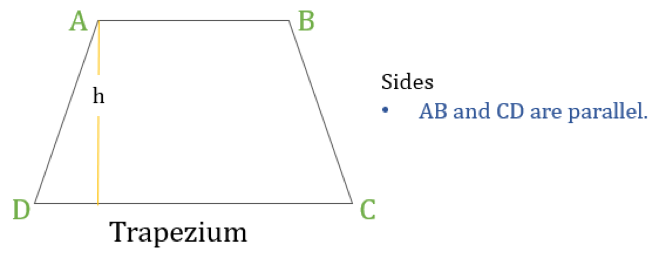
A trapéz tulajdonságai
A trapéz olyan négyszög, amelynek a következő egy tulajdonsága van:
- A szemben lévő oldalaknak csak egy párja párhuzamos egymással
Trapéz képletek – A trapéz területe és kerülete
Ha a trapéz magassága ‘h’ (ahogy a fenti ábrán látható), akkor:
- A trapéz kerülete = az összes oldal hosszának összege = AB + BC + CD + DA
- A trapéz területe = ½ × (A párhuzamos oldalak hosszának összege) × h = ½ × (AB + CD) × h
Ezek. gyakorló kérdések segítenek megszilárdítani a trapéz tulajdonságait
Négyszögek tulajdonságai
Az alábbi táblázatban összefoglaljuk a négyszögek eddig tanult tulajdonságait:
| Négyszögek tulajdonságai | Téglalap | Négyzet | Párhuzamos | Rombusz | Trapézium | ||
| Minden oldala egyenlő | ✖ | ✔ | ✖ | ✔ | ✖ | ||
| Egymással szembenálló Az oldalak egyenlőek | ✔ | ✔ | ✔ | ✔ | ✖ | ||
| Opposite Az oldalak párhuzamosak | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ |
| Minden szög egyenlő | ✔ | ✔ | ✖ | ✖ | ✖ | ||
| Az ellentétes szögek egyenlőek | ✔ | ✔ | ✔ | ✔ | ✖ | ✖ | |
| Két szomszédos szög összege 180 | ✔ | ✔ | ✔ | ✔ | ✖ | ||
| Megfelezik egymást | ✔ | ✔ | ✔ | ✔ | ✖ | ||
| Megfelezik egymást merőlegesen | ✖ | ✔ | ✖ | ✔ | ✖ |
Az alábbi kép is összefoglalja a négyszögek tulajdonságait:
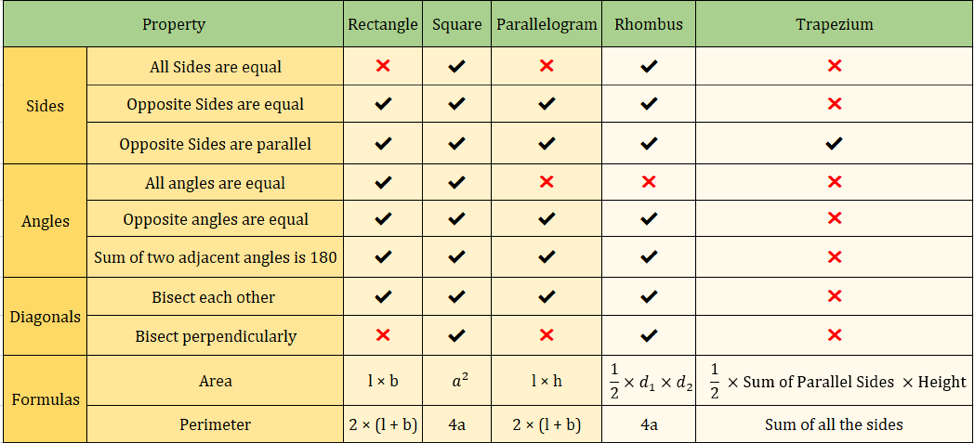
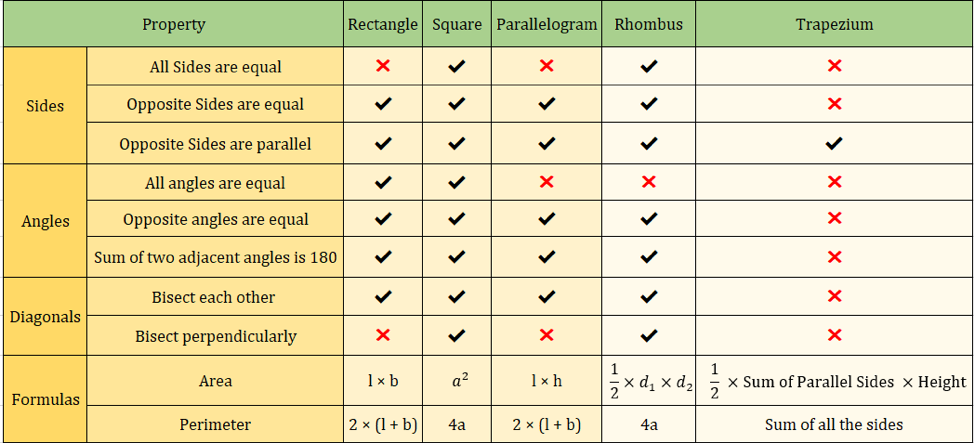
Fontos négyszögképletek
Az alábbi táblázat a különböző típusú négyszögek területére és kerületére vonatkozó képleteket foglalja össze:
| Négyszögek képletei | Téglalap | Négyzet | Parallelogramma | Rhombusz | Trapéz |
| Felület | l × b | a² | l × h | ½ × d1 × d2 | ½ × (Párhuzamos oldalak összege) × magasság |
| kerülete | 2 × (l + b) | 4a | 2 × (l + b) | 4a | Az oldalak összege |
További olvasmányok:
- A kör tulajdonságai | Körképletek – Terület és kerület
- A számok tulajdonságai – Páros & Páratlan | Prím | HCF & LCM
- A háromszögek tulajdonságai – Definíció | Típusok | Osztályozás
- Egyenesek és szögek – tulajdonságok és alkalmazásuk
Négyszögek kérdései
A négyszögek tulajdonságainak alkalmazását gyakoroljuk az alábbi mintakérdéseken:
1. kérdés
Adam egy 10 méter hosszú és 15 méter széles kerítést szeretne építeni a téglalap alakú kertje köré. Hány méter kerítést kell vásárolnia, hogy az egész kertet bekerítse?
- 20 méter
- 25 méter
- 30 méter
- 40 méter
- 50 méter
megoldás
1. lépés: Adott
- Adamnak van egy négyszögletes kertje.
- Hossza 10 méter, szélessége 15 méter.
- Kerítést akar építeni köré.
2. lépés: Meg kell találni
- Az egész kert körüli kerítés megépítéséhez szükséges hosszúságot.
3. lépés: Megközelítés és kidolgozás
A kerítés csak a kert külső oldalai köré építhető.
- A kerítés teljes szükséges hossza= A kert összes oldala hosszának összege.
- Mivel a kert téglalap alakú, az összes oldal hosszának összege nem más, mint a kert kerülete.
- Kerület = 2 × (10 + 15) = 50 méter
A kerítés szükséges hossza tehát 50 méter.
Ezért az E lehetőség a helyes válasz.
Kérdés: 2
Steve ki akarja festeni a szobája egyik téglalap alakú falát. A fal festésének költsége 1,5 dollár négyzetméterenként. Ha a fal 25 méter hosszú és 18 méter széles, akkor mennyi a fal festésének teljes költsége?
- $ 300
- $ 350
- $ 450
- $ 600
- $ 675
megoldás
1. lépés: Adott
- Steve a szobája egyik falát szeretné lefesteni.
- A fal 25 méter hosszú és 18 méter széles.
- A fal festésének költsége 1,5 dollár négyzetméterenként.
2. lépés: Megkeresni
- A fal festésének teljes költségét.
3. lépés: Megközelítés és kidolgozás
- A falat az egész területére festjük.
- Ha tehát megkeressük a fal teljes területét négyzetméterben, és megszorozzuk a fal 1 négyzetméterének festési költségével, akkor megkapjuk a teljes költséget.
- A fal területe = hossz × szélesség = 25 méter × 18 méter = 450 négyzetméter
- A fal festésének teljes költsége = 450 × 1 dollár.5 = 675 $
A helyes válasz tehát az E. lehetőség.
Reméljük, mostanra már megtanulta a négyszögek különböző típusait, tulajdonságaikat és képleteiket, valamint azt, hogyan alkalmazza ezeket a fogalmakat a négyszögekkel kapcsolatos kérdések megoldásához. A négyszögek alkalmazása fontos a GMAT geometriakérdéseinek megoldásához. Ha a GMAT vizsgát tervezi, segítünk Önnek kiváló minőségű tananyaggal, amelyhez ingyenesen hozzáférhet, ha itt regisztrál.
Itt van még néhány cikk a matematikáról:
- Növelje a pontosságot a sokszögekre vonatkozó matematikai kérdésekben
- Geometria kérdések – leggyakoribb hibák | GMAT Quant Prep
Ha a GMAT vizsgát tervezi, mi hozzáférést biztosítunk Önnek minőségi online tartalomhoz a felkészüléshez. Mi vagyunk a legjobban értékelt GMAT előkészítő cég a gmatclubon, több mint 1950 értékeléssel.
Miért nem veszel részt egy ingyenes próbavizsgán, és ítéld meg magad?
Írjon nekünk a [email protected] címre, ha bármilyen kérdése van.




