Entrópia – A termodinamika és az információelmélet pillére
Az entrópia egy homályos, mégis erőteljes kifejezés, amely a termodinamika és az információelmélet számos kulcsfontosságú gondolatának gerincét alkotja. Először a fizikai tudósok azonosították a 19. században, és az ipari forradalom számos forradalmi technológiájának vezérelveként szolgált. A kifejezés azonban az információs korszak elindításához is hozzájárult, amikor Claude Shannon matematikus A Mathematical Theory of Communication (A kommunikáció matematikai elmélete) című úttörő művében megjelent. Hogyan lehet tehát egy kifejezés felelős két áttörésért, körülbelül egy évszázad különbséggel, rokon, de mégis különböző területeken?
Először is, kezdjük azzal, hogyan értelmezik az entrópiát a fizikai tudományokban. A termodinamika első törvénye kimondja, hogy bármely zárt rendszerben az energia nem keletkezhet és nem semmisülhet meg. A második törvény, más néven az entrópia törvénye előírja, hogy egy nyitott rendszerben az energia mindig egy magasabb koncentrációból egy alacsonyabb koncentrációba áramlik a termodinamikai egyensúly elérése érdekében. Mit jelent ez a gyakorlatban? Azt jelenti, hogy a bögre kávé végül kihűl, és az italban lévő jég idővel elolvad, vagy hogy a tűzbe helyezett szerszám felmelegszik, mivel a láng energiája átadódik a vasmolekuláknak, de lehűl, amint eltávolítják, mivel az energia szétoszlik az új környezetében.

Az entrópia kifejezés maga egy adott rendszer rendezetlenségi állapotára utal. A koncentrált és felhasználható formában lévő energiát rendezettnek, míg az eloszló és hozzáférhetetlen formában lévő energiát rendezetlennek tekintjük.
Az entrópia csak egy irányba – az egyensúly felé – mozog, hacsak nem hat rá a rendszeren kívüli erő, és még akkor is, a külső erők, mint például a biológiai rendszerek, csak átmenetileg tudják megfordítani az entrópia folyamatát, és végül engednek (a halál révén). Bármely növény vagy állat egy összetett energiarendszer, amely az entrópia folyamatának ellensúlyozásával és a környezetből rendelkezésre álló, rendezett energia összegyűjtésével, majd a tápanyagoktól megfosztott hulladék kibocsátásával marad életben. De az élő rendszerben az átáramló energia végül lebontja a fizikai szerkezetét, aminek következtében a szervezet lebomlik és elpusztul (remélhetőleg a végső célját, a szaporodást teljesítve). Az energiatest, amely már nem él, lebomlik és szétoszlik a környező környezetbe – és a termodinamikai egyensúlyba.
Az entrópia elméletileg csak akkor hagyja abba egyenletes menetelését, ha elhozta a világegyetem hőhalálát – egy olyan végső végállapotot, ahol nincs szabad energia. A Földön és az űrben végül minden kitágul, felrobban, elpusztul, és egyenletesen szétosztja a szabad energiát abban, ami valójában a legnagyobb zárt rendszer: a világegyetemben. Ily módon az entrópia a gravitációhoz hasonló egyetemes törvény, mivel a biofizika legkisebb és legnagyobb léptékében is működik.”
A gazdaságok organizmusok, nem mosógépek
Az entrópia a gazdaságra is vonatkozik. Az entrópia folyamata egy organizmuson belül, azáltal, hogy a rendelkezésre álló energiát a környezetből megszerzi és rendezetlen energiává alakítja át, az organizmusok csoportjaira is igaz. A társadalmak az alacsony entrópiájú energiaforrásokat két formában veszik fel: készletek és áramlások formájában. A készletek közé tartoznak a ritkaföldfémek, a fosszilis tüzelőanyagok és más földi lelőhelyek, amelyeket évezredek alatt bonyolult, hosszú távú földi folyamatok hoztak létre. Az áramlások olyan megújuló forrásokból származnak, mint a szél, a víz és a napenergia, amelybe a biomassza is beletartozik (a napenergia közvetett kiterjesztéseként). Az egyes források természetéből adódóan a készletek mennyisége korlátozott, míg az áramlások mind mennyiségükben, mind sebességükben korlátozottak. A civilizációknak, akárcsak az organizmusoknak, anyagcseréjük van. Feldolgozzák az energiát.

Az ipari forradalom során a gazdaság elsődleges energiafelhasználása először az áramlásokról a földi készletekre tevődött át. A lóval hajtott szántókat és a szélvitorlákat, a munka két áramlásokra támaszkodó formáját felváltotta a gépesített mezőgazdaság és a gőzzel hajtott hajók, amelyek fosszilis tüzelőanyagokra támaszkodnak. Az évmilliók alatt megkövesedett, szunnyadó napenergiából tőkét kovácsoltunk, hogy megszabadítsuk a civilizációt a biológiai földi áramlások korlátaitól, és nyaktörő növekedést idézzünk elő a népesség és a GDP terén.
Az átállás tagadhatatlan gazdasági és anyagi előnyei ellenére mellékhatásként felgyorsította az entrópia folyamatát és növelte a rendezetlenséget az éghajlati rendszerben. Bár az energia összmennyisége a gazdasági folyamat során változatlan marad (a napenergia kivételével), a termelési folyamathoz szükséges ásványi anyagok bányászata és a fosszilis tüzelőanyagok fogyasztása olyan minőségi változást jellemez, amely az energiát a rendből a rendezetlenségbe helyezi át. Ily módon az entrópia képezi a szűkösség alapját, mivel az ember nem tudja az energiát fordítva, a rendezetlenség állapotából a rendezettség állapotába mozgatni; entrópia nélkül fizikailag lehetséges lenne a légköri CO2-t visszaalakítani széndarabkává, ahogyan lehetséges lenne a gumiabroncsnak az aszfalton való lebomlása során elvesztett gumirészecskék felfogása és újraképzése is.

Végeredményben a gazdaságunk dolgokat és energiát használ. Annak ellenére, hogy a pénz, az általunk képviselt érték a végtelenségig kering a gazdaságban, az általa képviselt fizikai javakra az entrópia törvénye érvényesül. A jelenlegi gazdasági rendszer olyan, mint egy szervezet, amely a végtelenségig növekszik. A szívünk pumpálja a vérünket, és életben tart minket, de ez az erő idővel elhasználja a sejtjeinket. Öregszünk és leépülünk.
Hogyan alkalmazható az entrópia az adattudományra?
Most már megnéztük, hogyan vonatkozik az entrópia az energiára, nézzük meg, hogyan alkalmazható a kommunikációra és az információelméletre. Szerintem ez a részlet Jimmy Soni és Rob Goodman Claude Shannon A Mind at Play című életrajzából egy remek anekdotikus történet az entrópia eredetéről:
Shannon az információ mint feloldott bizonytalanság gondolatával – amely később munkájának középpontjában állt – és egy szerény kérdéssel kereste meg a nagy embert. Hogy nevezze el ezt a dolgot? Von Neumann azonnal válaszolt: “Mondjuk, hogy az információ csökkenti az “entrópiát”. Egyrészt ez egy jó, szilárd fizikai szó. És ami még fontosabb – folytatta -, senki sem tudja, mi is az entrópia valójában, így egy vitában mindig előnyben leszel.”

Mielőtt Shannon entrópia-definíciójával foglalkoznánk, talán segít, ha lebontjuk az információ fogalmát. Shannon elméletének alapgondolata az, hogy egy közölt üzenet információs értéke attól függ, hogy az üzenet tartalma mennyire meglepő. Ennek remek gyakorlati példája a nyelvben a betűk gyakoriságának használata. Valószínűségi szempontból, ha egy betű előfordulása egy esemény, akkor minden adott esemény legvalószínűbb kimenetele ezt a valószínűségi eloszlást követi:
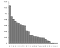
Minél több betű van, annál kevesebb a bizonytalanság az üzenetben. De ez függ a betű ritkaságától is. Például az alábbi üzenetek közül melyiknek van nagyobb információs ereje, az 1-nek vagy a 2-nek?
_AT
Az “1” lehetőség két viszonylag nagy valószínűségű betűt tartalmaz, ahol a hiányzó betű pótlásával mindenféle szót ki lehet írni: “Denevér”, “Macska”, “Kalap”, “Kövér”, “Sat” stb. A 2. lehetőség tartalmazza a viszonylag nehezen megfejthető “H” betűt, amelyből néhány szólehetőség marad, például “Kalap” vagy “Hit”, de nem olyan sok, mint az 1. lehetőség. Ezért a 2. lehetőség több információt közöl, mert nagyobb mértékben csökkenti a bizonytalanságot.”
Ha tehát az információ feloldott bizonytalanság, akkor az entrópiának kell lennie a feloldásra szoruló bizonytalanságnak. Egy esemény ritkasága, vagyis “meglepetésszerűsége” határozza meg az információtartalmát (ha játszottál már Scrabble-t, tudod, mennyire korlátozottak a lehetőségek, ha kihúzzuk a “Q” betűt). Minden alkalommal, amikor közlünk egy információdarabot, az általános entrópia, rendezetlenség, bizonytalanság, vagy nevezzük, ahogy akarjuk, arányosan vagy arányosan csökken. Mi is ez az arányos mennyiség?
Shannon kiszámította, hogy az egyes lehetséges adatértékekhez tartozó információs entrópia mértéke az értékhez tartozó valószínűségi tömegfüggvény negatív logaritmusa:
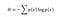
Az entrópia azt a várható információmennyiséget méri, amelyet egy véletlen esemény kimenetelének azonosítása közvetít, ahol a lehetséges kimenetek egy valószínűségi függvény. Ez azt jelenti, hogy a kockadobás nagyobb entrópiával rendelkezik, mint az érmefeldobás, mivel a kockadobás minden kimenetelének (⅙) kisebb a valószínűsége, mint a fej vagy írás (½). Az összefüggés grafikus szemlélete segít:

A fej eredmény közlésével tudjuk, hogy írás nem történt.
A gépi tanulásban az entrópia matematikai értelmezését számos algoritmus információnyereség-mérőszámának kiszámítására használják. A döntési fák például sok különböző attribútum, más néven jellemző vagy független változó közül választanak ki egyet, hogy a mintákat ismételten részhalmazokra osszák fel. Az algoritmus minden egyes felosztásnál kiválaszt egy attribútumot, amely alapján a mintát felosztja, és ezt addig folytatja, amíg az összes részhalmaz tiszta nem lesz, vagy más szóval, egy részhalmaz minden egyes mintája ugyanazt az osztályozási vagy célértéket kapja.
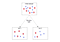
A minta részhalmaz tisztaságának méréséhez az algoritmusnak mennyiségi mérőszámra van szüksége, hogy objektíven kiválaszthassa, melyik jellemző alapján kell osztani minden egyes csomópontban. Itt jön a képbe az entrópia. Az algoritmus minden egyes lépésnél kiszámítja, hogy melyik attribútum mutatja a legnagyobb információnyereséget, majd dönt a felosztásról. Kiszámítja továbbá a bizonytalanság várható csökkenését a felosztás előtt és után; ha ez csökken, a felosztás megmarad, és az algoritmus a következő lépésre lép. Ha nem csökkent, akkor elérte a tisztaságot, és az algoritmus megáll. Ily módon az algoritmus felelős mind annak kiválasztásáért, hogy melyik jellemzőn kell osztani, mind pedig a folyamat megállításáért.
Létezik-e kapcsolat a termodinamika és az információelmélet között?
Az entrópia kérlelhetetlenül áramlik át egy döntési fán, ahogyan kérlelhetetlenül áramlik át egy csésze kávén a levegőbe. Az energiában a termodinamikai egyensúly felé menetel; az információelméletben a tisztaság felé menetel.
Az entrópia energiaértelmezése és az entrópia információelméleti értelmezése lényegében ugyanabban a pontban konvergál – a fizika alapvető törvényeiben. A kommunikációhoz energia kell, az energia felhasználásához pedig kommunikációra van szükség. Shannon szerint egy információ entrópiaértéke abszolút határt szab egy üzenet lehető legrövidebb átlagos hosszának, vagyis annak, hogy mennyire lehet tömöríteni az üzenetet anélkül, hogy az információ a továbbítás során elveszne. A félvezetők, a zseblámpák és a serpenyő morzeírással történő megkopogtatása emberi energiát igényel, és a kommunikációnk mindig a leghatékonyabb átviteli módra törekszik.
Az energiában az entrópiát úgy próbáljuk minimalizálni, hogy korlátozzuk, mennyit és milyen hatékonyan fogyasztunk. Célunk, hogy rendezett energiaforrásokat találjunk, és ellenálljunk az entrópia szervezetünkre gyakorolt hatásának. A kommunikációban az entrópiát az információk felkutatásával és a bizonytalanság csökkentésével minimalizáljuk. Bizonyos értelemben a rendezetlenség kommunikáción keresztüli csökkentésével megállíthatjuk az energia entrópikus folyamatát; egy vadászó-gyűjtögető a nyelv segítségével kommunikálhat egy másik emberrel, hogy figyelmeztesse, hogy egy oroszlán felfalja, csökkentve ezzel 1. az oroszlán hollétének bizonytalanságát (információs entrópia) és 2. az oroszlán általi megevés folyamatát (energia-entrópia). Ez a kommunikációs aktus csökkenti az összes lehetséges esemény valószínűségi terét, és lehetővé teszi számunkra, hogy hatékonyabban és eredményesebben cselekedjünk. A termodinamika és az információs korszak közötti összefüggések megértéséhez kulcsfontosságú annak megértése, hogyan működik ez az erőteljes törvény a digitális és a fizikai birodalomban.




