Hullámfüggvény definíciója
Az alapvető részecskék, például az elektronok, részecskeként vagy hullámként írhatók le.
Az elektronok hullámfüggvénnyel írhatók le, a hullámfüggvény szimbóluma a görög pszi, Ψ vagy ψ betű.

A Ψ hullámfüggvény egy matematikai kifejezés.Lényeges információt hordoz a hozzá tartozó elektronról:a hullámfüggvényből megkapjuk az elektron energiáját, szögimpulzusát és pályaorientációját az n, l és ml kvantumszámok formájában.
A hullámfüggvénynek lehet pozitív vagy negatív előjele.az előjel fontos a számításoknál.akkor is fontos, amikor két vagy több atom hullámfüggvénye egyesül molekulává.
A hasonló előjelű (fázisban lévő hullámok) hullámfüggvények konstruktívan interferálnak, ami a kötés lehetőségét eredményezi. a nem azonos előjelű (fázison kívüli) hullámfüggvények destruktívan interferálnak.
1926-ban Erwin Schrödinger levezette a legegyszerűbb atom, a hidrogén hullámfüggvényét. a Schrödinger-egyenlet megoldása lehetővé teszi a tudósok számára, hogy meghatározzák az atomok és molekulák elektronjainak hullámfüggvényeit.
A Schrödinger-egyenlet a kvantummechanika egyenlete: a kiszámított hullámfüggvényeknek diszkrét, megengedett értékei vannak az atomokban és molekulákban kötött elektronok számára;minden más érték tiltott.
A Ψ fontossága mellett annak négyzete, Ψ2 is óriási jelentőséggel bír a kémiában.
Ψ2 a valószínűségi sűrűség.megmondja, hogy az atommag körüli térben hol található az elektron a legnagyobb valószínűséggel.
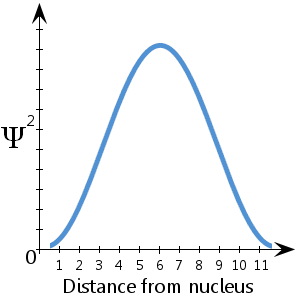
Az itt ábrázolt (fiktív) sematikus diagramon például, amely a Ψ2-t mutatja az atommagtól való távolság függvényében, azt látjuk, hogy az elektron nagy valószínűséggel az atommagtól körülbelül 5-7 egységnyi távolságra található.Azt is látjuk, hogy elenyészően kicsi a valószínűsége annak, hogy az elektron az atommagnál vagy az atommagtól több mint 11½ egységnyi távolságra legyen.
100 százalékos a valószínűsége annak, hogy az elektron valahol van – más szóval a valószínűsége 1.
Ψ csak az egy elektronnal rendelkező atomok, azaz a H, He+, Li2+, Be3+, B4+, C5+ stb. esetében számítható ki pontosan.Matematikai nyelven azt mondjuk, hogy Ψ analitikus megoldása csak az egyelektronos rendszerekre lehetséges.Az egyelektronos rendszereket gyakran hidrogénesnek – azaz “hidrogénszerűnek” – nevezik.”
A többi atom, ion és molekula esetében nem lehetséges analitikus megoldás a Ψ-re;a kiszámításához közelítő módszerek szükségesek.
Ψ2 és hidrogénes orbitálisok
A hidrogén valószínűségi sűrűségét ábrázolva (i.azaz Ψ2) különböző kvantumszámok esetén lehetővé teszi, hogy szemléltessük az elektronok által elfoglalt, az atommagra központosított teret.A különböző Ψ2 eloszlások a hidrogén elektronpályái.A ténylegesen elfoglalt pályát az határozza meg, hogy mekkora energiával rendelkezik az elektron.
Példák a hidrogén pályáira
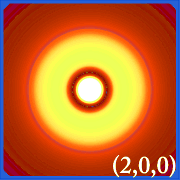
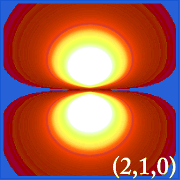

.









