Kezdő algebra
Tanulási célok
- Rendezett párok ábrázolása
- A koordinátasík összetevőinek azonosítása
- Rendezett párok ábrázolása a koordinátasíkon
.
- Kvadránsok azonosítása a koordinátasíkon
- A koordinátasík négy kvadránsának azonosítása
- Adott egy rendezett pár, határozd meg a kvadránsát
A koordinátasíkot évszázadokkal ezelőtt (egészen pontosan 1637-ben) fejlesztette ki és finomította René Descartes francia matematikus. Az ő tiszteletére a rendszert néha kartéziánus koordinátarendszernek nevezik. A koordinátasík pontok és egyenesek ábrázolására használható. Ez a rendszer lehetővé teszi az algebrai összefüggések vizuális leírását, valamint segít az algebrai fogalmak létrehozásában és értelmezésében.
A koordinátasík összetevői
Valószínűleg használtál már korábban koordinátasíkot. Használtál-e már például valaha rácsos felületi síkot egy tárgy helyzetének feltérképezésére? (Ezt gyakran teszik az úti térképeknél is.)

Ez a “térkép” egy vízszintes és függőleges rácshálót használ, hogy információt közvetítsen egy objektum helyzetéről. Figyeljük meg, hogy az A-F betűk a tetején, az 1-6 számok pedig a bal szélén szerepelnek. Ezen a térképen bármely tárgy általános helyét meg lehet találni a rácsnégyzet betűjének és számának segítségével. Például a “4F” négyzetben található elemet úgy találhatod meg, ha az ujjadat a vízszintes mentén az F betűig mozgatod, majd egyenesen lefelé, hogy egy vonalban legyél a 4-essel. A térképen ezen a helyen egy kék korong található.
A koordinátasík hasonló elemekkel rendelkezik, mint a fent látható rács. Egy vízszintes és egy függőleges tengelyből, számvonalakból áll, amelyek derékszögben metszik egymást. (Merőlegesek egymásra.)
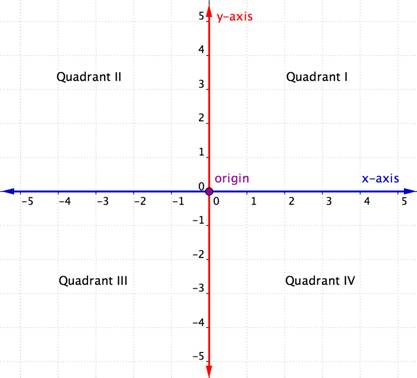
A koordinátasík vízszintes tengelyét x-tengelynek nevezzük. A függőleges tengelyt y-tengelynek nevezzük. Azt a pontot, ahol a két tengely metszi egymást, origónak nevezzük. Az origó az x-tengelyen 0, az y-tengelyen 0.
A koordinátasíkon lévő helyeket rendezett párokkal írjuk le. Egy rendezett pár egy pont helyét úgy mondja meg, hogy a pont helyét az x-tengely (a rendezett pár első értéke) és az y-tengely (a rendezett pár második értéke) mentén viszonyítja egymáshoz.
Egy rendezett párban, például (x, y), az első értéket x-koordinátának, a második értéket pedig y-koordinátának nevezzük. Vegyük észre, hogy az x-koordináta az y-koordináta előtt szerepel. Mivel az origó x-koordinátája 0, y-koordinátája pedig 0, a rendezett párját (0, 0) írjuk.
Nézzük meg az alábbi pontot.

A pont helyének meghatározásához kezdjük az origónál (0, 0), és haladjunk jobbra az x-tengely mentén, amíg a pont alá nem érünk. Nézze meg az x-tengelyen lévő címkét. A 4 azt jelzi, hogy az origótól négy egységet haladtunk jobbra az x-tengely mentén. Ez az x-koordináta, az első szám a rendezett párban.
Az x-tengelyen a 4-től haladj felfelé a ponthoz, és figyeld meg, hogy az y-tengelyen milyen számmal van egy vonalban. A 3 azt jelzi, hogy az x-tengely elhagyása után 3 egységet haladtál felfelé függőleges irányban, az y-tengely irányában. Ez a szám az y-koordináta, a rendezett pár második száma. Ha az x-koordináta 4 és az y-koordináta 3, akkor a (4, 3) rendezett párral rendelkezünk.
Nézzünk egy másik példát.
Példa
Írd le az ábrázolt pontot rendezett párként.

Írd le a rendezett párként ábrázolt pontot
Pontok ábrázolása a koordinátasíkban
Most már tudod, hogyan kell használni az x- és y-tengelyt, tudsz rendezett párt is ábrázolni. Csak ne feledd, hogy mindkét eljárás az origóból – az elejéről – indul! A következő példa azt mutatja, hogyan kell ábrázolni a (1,3) rendezett párt.
Példa
Plotáld a (1, 3) pontot.
Az előző példában az x- és az y-koordináta is pozitív volt. Ha egy rendezett pár egyik (vagy mindkét) koordinátája negatív, akkor az egyik vagy mindkét tengely mentén negatív irányban kell mozogni. Tekintsük az alábbi példát, amelyben mindkét koordináta negatív.
Példa
Rajzoljuk a (-4,-2) pontot.

Az x-koordináta -4, mert a rendezett párban ez áll az első helyen. Induljunk az origóból, és mozogjunk 4 egységgel negatív irányba (balra) az x-tengely mentén.
Az y-koordináta -2, mert ez a második a rendezett párban. Most mozgassunk 2 egységet negatív irányba (lefelé). Ha az y-tengelyre nézünk, akkor azon a tengelyen a -2-vel kell egy vonalba kerülnünk.
A pont ábrázolásának lépéseit az alábbiakban foglaljuk össze.
Lépések egy rendezett pár (x, y) ábrázolásához a koordinátasíkon
- Meghatározzuk az x koordinátát. Az origóból kiindulva mozogjunk vízszintesen, az x-tengely irányában, az x-koordináta által megadott távolságot. Ha az x-koordináta pozitív, mozogjunk jobbra; ha az x-koordináta negatív, mozogjunk balra.
- Meghatározzuk az y-koordinátát. Az x-koordinátától kezdve mozogjunk függőlegesen, az y-tengely irányában, az y-koordináta által megadott távolságot. Ha az y-koordináta pozitív, lépjünk felfelé; ha az y-koordináta negatív, lépjünk lefelé.
- Rajzoljunk egy pontot a végpont helyén. Címkézze a pontot a rendezett párral.
Pontok ábrázolása a koordinátasíkon
Kijelölje a kvadránsokat, és használja őket pontok ábrázolásához
A koordinátasíkot a metsző x- és y-tengelyek négy szakaszra osztják. Ezt a négy szakaszt kvadránsoknak nevezzük. A kvadránsokat az I, II, III és IV római számokkal nevezzük el, a jobb felső kvadránstól kezdve az óramutató járásával ellentétes irányban haladva.
A bármely kvadránson belüli rendezett pároknak vannak bizonyos közös jellemzőik. Nézd meg az alábbi grafikonon az egyes kvadránsokat. Mit veszel észre az egyes kvadránsokon belüli pontok x- és y-koordinátáinak előjelében?
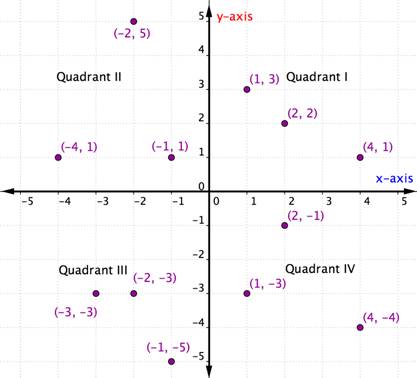
Az egyes kvadránsokon belül az egyes rendezett párok x- és y-koordinátáinak előjele megegyezik. Ezek is egy mintát követnek, amelyet az alábbi táblázatban vázolunk fel.
| Kvadráns | A pont általános formája ebben a kvadránsban | Példa | Megnevezés |
|---|---|---|---|
| I | (+,+) | (5,4) | Az origóból kiindulva haladjunk az x-tengelyen pozitív irányba (jobbra) és az y-tengelyen pozitív irányba (felfelé). |
| II | (-,+) | (-5,4) | Az origóból kiindulva haladjunk az x-tengely mentén negatív irányba (balra) és az y-tengely mentén pozitív irányba (felfelé). |
| III | (-,-) | (-5,-4) | Az origóból kiindulva haladjunk az x-tengely mentén negatív irányba (balra) és az y-tengely mentén negatív irányba (lefelé). |
| IV | (+,-) | (5,-4) | Az origóból kiindulva haladjunk az x-tengely mentén pozitív irányba (jobbra) és az y-tengely mentén negatív irányba (lefelé). |
Ha már ismered a kvadránsokat a koordinátasíkban, akkor a fenti diagram alapján anélkül is meghatározhatod egy rendezett pár kvadránsát, hogy grafikusan ábrázolnád. Íme egy másik gondolatmenet:
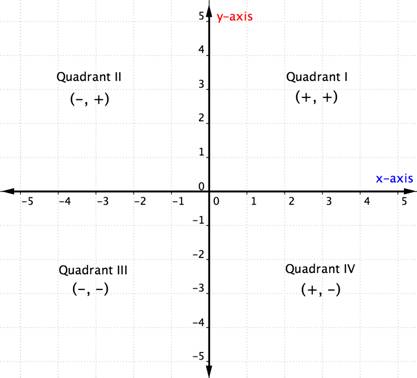
Az alábbi példa részletezi, hogyan határozhatjuk meg egy pont kvadránsbeli elhelyezkedését pusztán a koordináták előjelére gondolva. Ha egy pont kirajzolása előtt végiggondolja a kvadráns helyét, elkerülheti a hibát. Hasznos tudás ez annak ellenőrzéséhez is, hogy helyesen ábrázoltunk-e egy pontot.
Példa
Melyik kvadránsban található a (-7,10) pont?
Példa
Melyik kvadránsban található a (-10,-5) pont?
Mi történik, ha egy rendezett pár x- vagy y-koordinátája nulla? Az alábbi példa a (0,4) rendezett pár grafikonját mutatja.
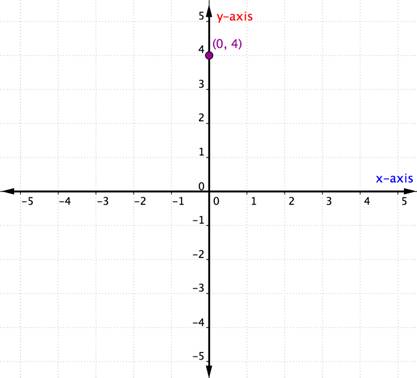
Az egyik tengelyen elhelyezkedő pont nem tekinthető kvadránsban lévőnek. Egyszerűen csak az egyik tengelyen van. Ha az x-koordináta 0, akkor a pont az y-tengelyen helyezkedik el. Hasonlóképpen, minden olyan pont, amelynek y-koordinátája 0, az x-tengelyen helyezkedik el.
A kvadránsok azonosítása és felhasználása pontok ábrázolásához
Összefoglaló
A koordinátasík a pontok és egyenesek ábrázolására és leírására szolgáló rendszer. A koordinátasík egy vízszintes (x-) és egy függőleges (y-) tengelyből áll. Ezeknek a vonalaknak a metszéspontja alkotja az origót, amely a (0,0) pont. A koordinátasík négy kvadránsra van osztva. A koordinátarendszer ezen jellemzői együttesen lehetővé teszik a pontokról, egyenesekről és más algebrai fogalmakról való grafikus ábrázolást és kommunikációt.





