Skewness – Gyors bevezetés, példák és képletek
A szkewness egy olyan szám, amely jelzi, hogy egy változó milyen mértékben
az aszimmetrikus eloszlású.
- Pozitív (jobb oldali) ferdeség példa
- Negatív (bal oldali) ferdeség példa
- Népesség ferdeség – képlet és számítás
- Minta ferdeség – képlet és számítás
- Minta ferdeség – képlet. Képlet és számítás
- Skewness in SPSS
- Skewness – Implikációk az adatelemzésre
Pozitív (jobb) Skewness példa
Egy tudósnak 1,000 emberrel néhány pszichológiai tesztet végeztet. Az 5. teszt esetében a teszteredmények ferdesége = 2,0. Ezeknek a pontszámoknak a hisztogramja az alábbiakban látható.
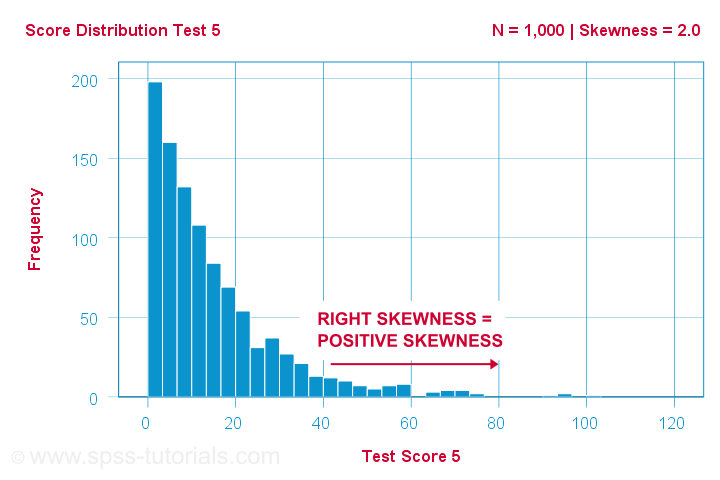
A hisztogram nagyon aszimmetrikus gyakorisági eloszlást mutat. A legtöbb ember 20 pontot vagy annál kevesebbet ér el, de a jobb oldali farok 90 pontig vagy annál is tovább nyúlik. Ez az eloszlás jobbra ferde.
Ha az x-tengelyen jobbra haladunk, akkor 0-tól 20 ponton át 40 pontig és így tovább. Tehát a grafikon jobb oldala felé haladva a pontszámok pozitívabbá válnak. Ezért a jobbra ferdeség pozitív ferdeség, ami azt jelenti, hogy a ferdeség > 0. Ennek az első példának a ferdessége = 2,0, amint azt a grafikon jobb felső sarka jelzi. A pontszámok erősen pozitívan ferdék.
Negatív (bal oldali) ferdeség példa
Egy másik változó – a 2-es teszt pontszámai kiderül, hogy a ferdeség = -1,0. A hisztogramjuk az alábbiakban látható.

A pontszámok nagy része 60 és 100 között van. A bal oldali farok azonban kissé megnyúlik. Tehát ez az eloszlás balra ferde.
Jobbra: balra, balra. Ha az x-tengelyt balra követjük, akkor a negatívabb pontszámok felé haladunk. Ezért van az, hogy a bal oldali ferdeség negatív ferdeség.És valóban, a ferdeség = -1,0 ezeknél a pontszámoknál. Eloszlásuk balra ferde. Azonban kevésbé ferde -vagy szimmetrikusabb-, mint az első példánk, amelynek ferdeség = 2,0.
A szimmetrikus eloszlás nulla ferdeséget feltételez
A szimmetrikus eloszlások ferdessége = 0. A 3. teszt pontszámai -a ferdeség = 0,1- közel állnak ehhez.

A megfigyelt eloszlások ritkán pontosan szimmetrikusak. Ez leginkább néhány elméleti mintavételi eloszlásnál figyelhető meg. Néhány példa:
- a (standard) normális eloszlás;
- a t-eloszlás és
- a binomiális eloszlás, ha p = 0,5.
Ezek az eloszlások mind pontosan szimmetrikusak, tehát ferdeségük =0.000…
Populáció ferdeség – képlet és számítás
Ha egy vagy több változóra szeretnénk kiszámítani a ferdeséget, akkor a számításokat bízzuk valamilyen szoftverre. De -csak a teljesség kedvéért- azért felsorolom a képleteket.
Ha az adatai a teljes populációt tartalmazzák, számítsa ki a populáció ferdeségét a következőképpen:
$$$Populáció\;ferdeség = \Sigma\biggl(\frac{X_i – \mu}{\sigma}\biggr)^3\cdot\frac{1}{N}$$
ahol
- \(X_i\) minden egyes egyéni pontszám;
- \(\mu\) a populáció átlaga;
- \(\sigma\) a populáció szórása és
- \(N\) a populáció mérete.
Egy példaszámításhoz, amely ezt a képletet használja, lásd ezt a Googlesheet-et (alább látható).
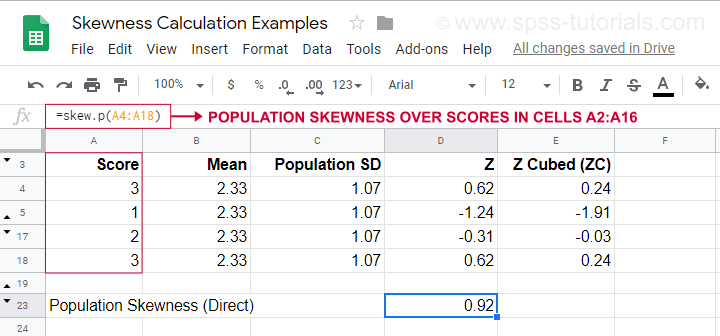
Ez azt is megmutatja, hogyan kaphatjuk meg közvetlenül a populáció ferdeségét a=SKEW.P(…)-vel, ahol a “.P” a “populációt” jelenti. Ez megerősíti a kézi számításunk eredményét. Sajnos sem az SPSS, sem a JASP nem számítja ki a populációs ferdeséget: mindkettő a minta ferdeségére korlátozódik.
Minta ferdeség – képlet és számítás
Ha adatai egyszerű véletlen mintát tartalmaznak valamilyen populációból, használja a
$$$Sample\;ferdeség = \frac{N\cdot\Sigma(X_i – \overline{X})^3}{S^3(N – 1)(N – 2)}$$
ahol
- \(X_i\) minden egyes pontszám;
- \(\overline{X}\) a minta átlaga;
- \(S\) a minta szórása és
- \(N\) a minta mérete.
Egy számítási példa látható ebben a Googlesheetben (alább látható).
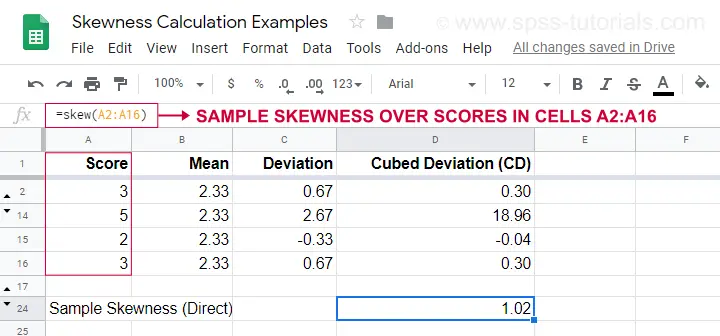
Egy egyszerűbb lehetőség a minta ferdeségének meghatározására a=SKEW(…).használata, amely megerősíti a kézi számításunk eredményét.
Skewness in SPSS
Először is, a “ferdeség” az SPSS-ben mindig a minta ferdeségére utal: csendben feltételezi, hogy az adataink egy mintát tartalmaznak, nem pedig a teljes populációt. Rengeteg lehetőség van a megszerzésére. Az én kedvencem a MEANS segítségével, mert a szintaxis és a kimenet tiszta és egyszerű. Az alábbi képernyőképek végigvezetik Önt.

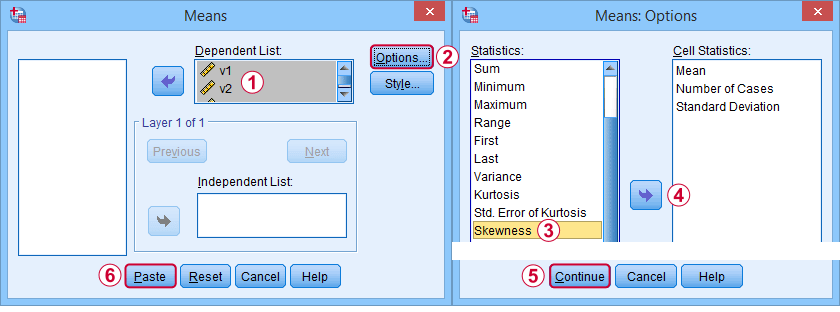
A szintaxis lehet olyan egyszerű, mintmeans v1 to v5
/cells skew.A nagyon teljes táblázat – beleértve az átlagokat, szórásokat, mediánokat és egyebeket – ameans v1 to v5
/cells count min max mean median stddev skew kurt.Az eredmény az alábbiakban látható.
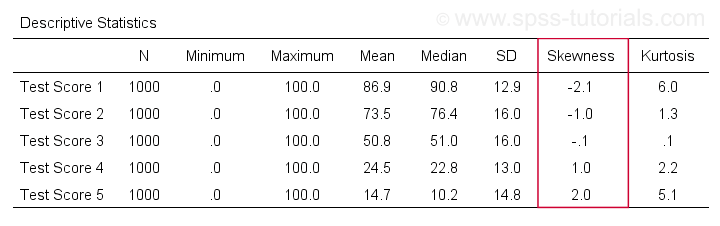
Skewness – Implikációk az adatelemzésre
Néhány elemzés -ANOVA, t-tesztek, regresszió és mások- megköveteli a normalitás feltételezését: a változóknak normálisan kell eloszlaniuk a populációban. A normális eloszlás ferdeség = 0. Ha tehát jelentős ferdeséget figyelünk meg néhány mintaadatban, az arra utal, hogy a normalitás feltételezése sérült.
A normalitás ilyen jellegű megsértése nem jelent problémát nagy mintanagyságok esetén – mondjuk N > 20 vagy 25 vagy hasonló. Ebben az esetben a legtöbb teszt robosztus az ilyen jogsértésekkel szemben. Ez a központi határértéktételnek köszönhető. Röviden,nagy mintaméretek esetén a ferdeség
nem jelent valódi problémát a statisztikai tesztek számára.A ferdeség azonban gyakran nagy szórással jár együtt. Ezek nagy standard hibákat és alacsony statisztikai erőt eredményezhetnek. Mint ahogyan így a jelentős ferdeség csökkentheti annak az esélyét, hogy valamilyen nullhipotézist elutasítsunk valamilyen hatás kimutatása érdekében. Ebben az esetben egy nemparametrikus teszt bölcsebb választás lehet, mivel nagyobb erővel rendelkezhet.A normalitás megsértése valós veszélyt jelent
kis mintanagyságú minták esetében – mondjuk- N < 20 vagy annál nagyobb. Kis mintanagyság esetén sok teszt nem robusztus a normalitás feltételezés megsértésével szemben. A megoldás -még egyszer- a nemparametrikus tesztek használata, mert ezek nem követelik meg a normalitást.
Végül, de nem utolsósorban, nincs statisztikai teszt annak vizsgálatára, hogy a populáció ferdeség = 0. Ennek vizsgálatára közvetett módon egy normalitásvizsgálat, mint például
- a Kolmogorov-Smirnov-féle normalitásvizsgálat és
- a Shapiro-Wilk-féle normalitásvizsgálat szolgál.
Amikor azonban valóban szükség van a normalitásra – kis mintanagyságok esetén -, az ilyen tesztek ereje alacsony: előfordulhat, hogy nem érnek el statisztikai szignifikanciát még akkor sem, ha a normalitástól való eltérések súlyosak. Így főként hamis biztonságérzetet nyújtanak.




