Szintetikus osztásmód
Meg kell mondanom, hogy a szintetikus osztás a polinomok osztásának “legszórakoztatóbb” módja. Kevesebb lépéssel jutunk el a válaszhoz, mint a polinomok hosszú osztásmódjánál. Ebben a leckében öt (5) példát fogok átnézni, amelyek remélhetőleg megismertetik Önt a polinomok szintetikus osztással történő sikeres osztásának alapvető eljárásaival.
Megjegyzendő dolgok:
- Győződjön meg róla, hogy az osztószám standard formában van. Ez azt jelenti, hogy a hatványok csökkenő sorrendben vannak.
- Az osztónak az x – \bal( c \jobb) alakban kell lennie.
Példák arra, hogyan oszthatunk polinomokat a szintetikus osztás segítségével
1. példa: Osszuk el az alábbi polinomot.
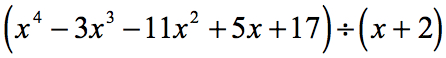
Vizsgáljuk meg újra az adott feladatot, és végezzük el a szükséges módosításokat, ha szükséges.
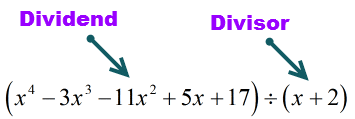
Az osztandó (az osztandó anyag) standard formában van, mert az exponensek csökkenő sorrendben vannak. Ez jó!
Az osztót át kell írni
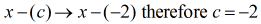
Ezzel a ponttal már fel tudom állítani a szintetikus osztást úgy, hogy kivonom az osztó együtthatóit, majd sorba állítom őket.
Közvetlenül a bal oldalra helyezzük a “dobozba” a c = – 2 értékét.
Végül konstruáljunk egy vízszintes vonalat közvetlenül az osztó együtthatói alá.
Lépések:
1. Dobjuk az első együtthatót a vízszintes vonal alá.
2. Szorozzuk meg ezt a dobott számot a “dobozban” lévő számmal. Bármi is legyen a szorzata, helyezd a vízszintes vonal fölé, közvetlenül a második együttható alá.
3. Add össze a számok oszlopát, majd az összeget tedd közvetlenül a vízszintes vonal alá.
4. Ismételd a folyamatot, amíg el nem fogynak az összeadandó oszlopok.
Lásd az alábbi animált megoldást:
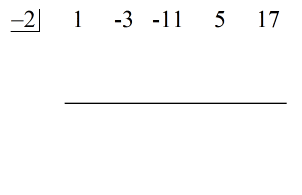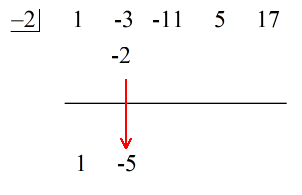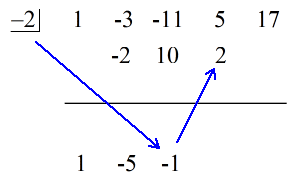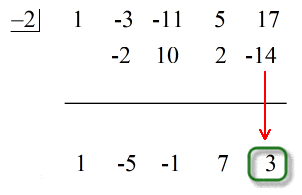
A vízszintes vonal alatti utolsó szám mindig a maradék! A maradék ebben a feladatban 3.
Hogyan ábrázoljuk tehát a végső válaszunkat?
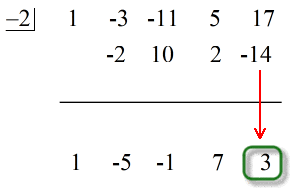
- A végső válaszodat ábrázold
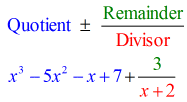
Megjegyezzük, hogy a vízszintes vonal alatti számok az utolsó (maradék) kivételével a hányados együtthatói.
Mégpedig a hányados változóinak az exponenseit mind 1-gyel csökkentjük.
2. példa: Osszuk el a polinomot.
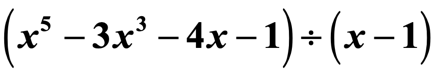
Ez nem beugratós kérdés. Figyeljük meg, hogy a hányados nem tartalmazza az x változó összes exponensét.
Látható, hogy hiányzik {x^4} és {x^2}. Ahhoz, hogy az x változó összes együtthatója csökkenő hatványon szerepeljen, az eredeti feladatot így kell átírnunk. Csatoljunk nullákat ezekhez a hiányzó x-ekhez. Az osztót is fejezzük ki x – (c) alakban, amiből egyértelműen kiderül c értéke, vagyis c = + 1.
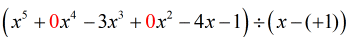
Ezután már felállíthatom a számokat, hogy folytassam a folyamatot.
Lépések:
1. Dobd az első együtthatót a vízszintes vonal alá.
2. Szorozd meg ezt a dobott számot a “dobozban” lévő számmal. Bármi is legyen a szorzata, helyezd a vízszintes vonal fölé, közvetlenül a második együttható alá.
3. Add össze a számok oszlopát, majd az összeget tedd közvetlenül a vízszintes vonal alá.
4. Ismételd a folyamatot, amíg el nem fogynak az összeadandó oszlopok.
Lásd az alábbi animált megoldást:
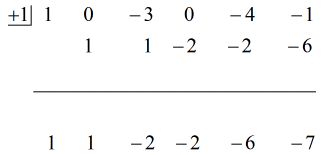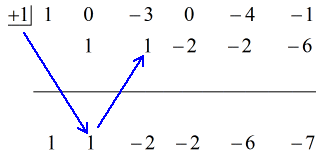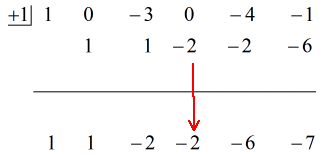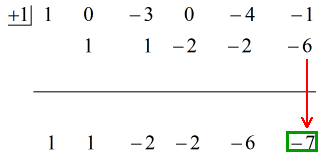
A végső választ így a
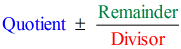
formába téve
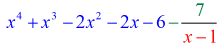
Példa 3: Osszuk az alábbi polinomot.
\left( { – 2{x^4} + x} \right) \div \left( {x – 3} \right)
Ez egyre érdekesebb! Az idézőjel határozottan borzalmasan néz ki, mert sok minden hiányzik belőle. Nemcsak néhány x hiányzik belőle, amelyek {x^3} és {x^2}, hanem a konstans is eltűnt.
Azért, hogy ezt kijavítsam, átírom az eredeti feladatot úgy, hogy minden x-et figyelembe vegyünk. De ami még fontosabb, ne felejtsük el a hiányzó állandót is belevenni, ami nulla.
Az “új és javított” feladatnak így kell kinéznie:
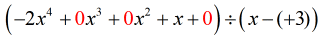
Tovább a szokásos módon haladjunk a lépésekkel.
Lépések:
1. Dobd le az első együtthatót a vízszintes vonal alá.
2. Szorozd meg ezt a ledobott számot a “dobozban” lévő számmal. Bármi is legyen a szorzata, helyezd a vízszintes vonal fölé, közvetlenül a második együttható alá.
3. Add össze a számok oszlopát, majd az összeget tedd közvetlenül a vízszintes vonal alá.
4. Ismételd a folyamatot, amíg el nem fogynak az összeadandó oszlopok.
Lásd az alábbi animált megoldást:
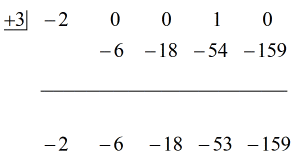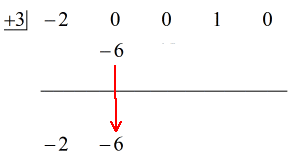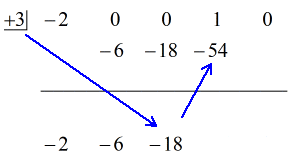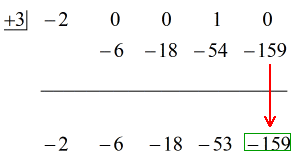
Oké, akkor a végső válasz erre
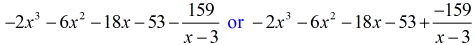
A végső választ kétféleképpen is leírhatod. Az első a mínusz vagy kivonási szimbólummal jelzi, hogy a maradék negatív. A második a + szimbólumot használja, de a számlálóhoz negatív szimbólumot csatol. Ezek ugyanazt jelentik!
4. példa: Oszd el az alábbi polinomot.
\left( { – {x^5} + 1} \right) \div \left( {x + 1} \right)
Ne csüggedj ezen a feladaton. Ez valójában elég könnyű, különösen most, hogy már végigmentél néhány példán. Ne felejtsd el mindig “kitölteni a hiányzó részeket”, igaz?
Nézd meg az osztalékot, és egyet kell értened abban, hogy a hiányzó részek {x^4}, {x^3}, {x^2} és x.
Újraírva az eredeti feladatot, amely szintetikus osztásra kész, megkapjuk…
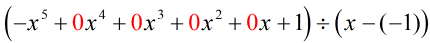
A hiányzó x-eket nullákkal töltöttük fel, és explicit módon megoldjuk c = -1-re.
Lépések:
1. Dobjuk az első együtthatót a vízszintes vonal alá.
2. Szorozzuk meg ezt a dobott számot a “dobozban” lévő számmal. Bármi is legyen a szorzata, helyezd a vízszintes vonal fölé, közvetlenül a második együttható alá.
3. Add össze a számok oszlopát, majd az összeget tedd közvetlenül a vízszintes vonal alá.
4. Add össze a számok oszlopát, majd az összeget helyezd közvetlenül a vízszintes vonal alá.
4. Ismételd a folyamatot, amíg el nem fogynak az összeadandó oszlopok.
Lásd az alábbi animált megoldást:
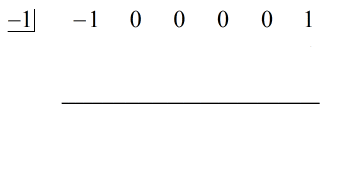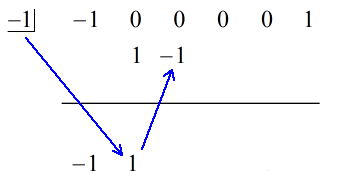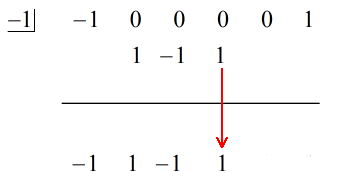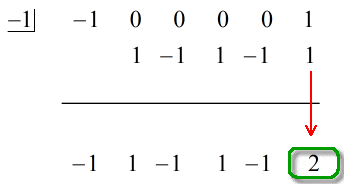
A vízszintes vonal alatti utolsó szám mindig a maradék lesz. Ezt ne felejtsd el! Ebben az esetben a maradék egyenlő 2-vel.
A végső válaszunk
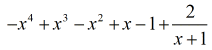
5. példa: Osszuk a polinomot egy binommal.
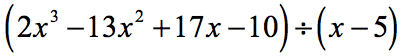
Ebben a példában a maradék nulla lesz. Ilyenkor az osztó az osztott tényezőjévé válik. Más szóval az osztó egyenlően osztja az osztalékot.
A feladatot megvizsgálva azt látom, hogy nincsenek hiányzó összetevők. Az x-ek minden hatványát figyelembe vettük, és van egy konstansunk. Ez nagyszerű! Ez a feladat tulajdonképpen készen áll a szintetikus osztásra.
Lépések:
1. Dobjuk az első együtthatót a vízszintes vonal alá.
2. Szorozzuk meg ezt a dobott számot a “dobozban” lévő számmal. Bármi is legyen a szorzata, helyezd a vízszintes vonal fölé, közvetlenül a második együttható alá.
3. Add össze a számok oszlopát, majd az összeget tedd közvetlenül a vízszintes vonal alá.
4. Ismételd a folyamatot, amíg el nem fogynak az összeadandó oszlopok.
Lásd az alábbi animált megoldást:
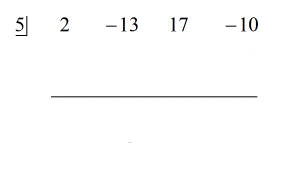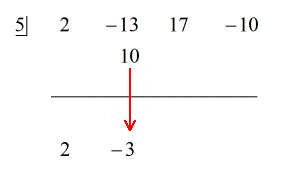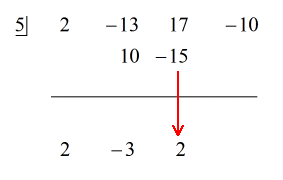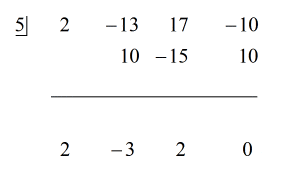
Mert a maradék egyenlő nullával, ez azt jelenti, hogy az x – 5 osztó az osztottnak egy tényezője
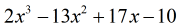
ezért
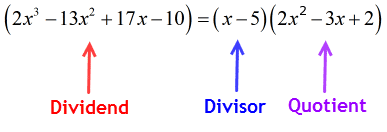
Munkalapokkal gyakorolni
Ez is érdekelhet:
Polinomok összeadása és kivonása
Polinomok osztása a hosszú osztás módszerével
Binomiálisok szorzása a FOIL módszerrel
Polinomok szorzása
.




