Várható pénzbeli érték
A várható pénzbeli érték elemzés (EMV) a kockázatkezelés statisztikai technikája, amelyet a kockázatok számszerűsítésére használnak. Ez a technika segít meghatározni a szükséges teljes készenléti tartalékot. Ezt a tartalékot azután a teljes projektterv részévé teszik.
A kockázatok lehetőségként és fenyegetésként kategorizálhatók. A lehetőségeket pozitív kockázati értékek, míg a fenyegetéseket negatív kockázati értékek fejezik ki. A kockázatértékeléshez kockázatsemleges feltételezéssel kell rendelkeznie a lehetőségek és a fenyegetések közötti helyes megítéléshez.
Két dolgot használunk itt.
- valószínűség
- hatás
Először ezeket kell megértenünk…
Mi a valószínűség?
Ez bármely esemény bekövetkezésének valószínűsége.
Egy dobásnál például a fej kimenetele 50% & így 50% a faroké.
Ezt kapjuk, mivel az események teljes száma 2, és így a fej vagy a farok valószínűsége 1/2.
Hasonlóképpen, ha dobunk egy kockát, akkor a valószínűsége bármely számnak, például a 3-asnak 1/6, mivel a kocka összes oldala 6-os. Ez 16,67% esélyt ad arra, hogy bármelyik számot megkapjuk a kockán.
A valószínűség egyértelmű.
Mi a hatás?
Ez egyszerűen az a pénzösszeg, amire szükségünk van az azonosított kockázat kezeléséhez, ha az bekövetkezik.
Például a projekt végrehajtása során azonosítjuk, hogy a berendezésben meghibásodás következhet be, és ki kell cserélnünk egy új berendezésre. Az új berendezés költsége pedig 5000 $. Ez a hatás értéke.
Ez lehet költséghatás vagy az ütemezés hatása (Az idő pénz).
Hogyan számítjuk ki az EMV-t?
A várható pénzbeli értéket bármely projekt esetében úgy számítjuk ki, hogy az egyes eredmények bekövetkezésének valószínűségét megszorozzuk az egyes lehetséges eredmények értékével & annak hatásával:
EMV = P x I
P = Az egyes eredmények bekövetkezésének valószínűsége.
I = Az egyes lehetséges kimenetek értéke
Egyszerű példa;
Egy alapvető példán keresztül próbálom elmagyarázni ezt a fogalmat;
1. lépés: Az összes tevékenység/feladat, az erőforrások költsége a mennyiségi jegyzékből (BOQ)
2. lépés: A projekthez kapcsolódó összes kockázati tényező elemzése
3. lépés: Az összes kockázat valószínűségének megtekintése. Lehetőségek & veszélyek mindkettő
Szint – 4: Számítsuk ki az összes azonosított kockázatra a rendkívüli tartalékot
Szint – 5: Adjuk össze az összeset, és kész is vagyunk
Lássuk az alábbi táblázatban; 5 kockázatot azonosítottunk. A 2. kockázat & 3 olyan lehetőség, amelyet ki kell használnunk ahhoz, hogy bekövetkezzen, a másik három pedig olyan fenyegetés, amelyet mérsékelnünk, elkerülnünk vagy át kell hárítanunk.
| Kockázat | valószínűség | hatás ($) | EVM (P*I) |
| 1 | 13% | -10,000 | -1300 |
| 2 | 10% | 20,000 | 2,000 |
| 3 | 25% | 25,000 | 6,250 |
| 4 | 15% | -2,50,000 | -37,500 |
| 5 | 80% | -1,500 | -1200 |
| -2,16,500 | -31,750 |
Kaptunk egy számot a hatásról, ami -216500, de ezt nem kell tartalékolnunk, mivel az EMV-t fogjuk kiszámítani, és az -31750.
Ezt kell tartalékolnunk tartalékként.
Remélem, most már teljesen világos.
Valószínűségi &hatásmátrix
Amint azt fentebb kifejtettük, ez a kvantitatív kockázatelemzési folyamat egyik legfontosabb eszköze. Elsődleges célja, hogy végül pénzt különítsen el a Költségalapban (a költségvetésben) – azaz a Kockázati tartalékban – a kockázat fedezésére. Ehhez a P-I Mátrix minőségi hatásskáláit az előző folyamat során magas prioritásúnak ítélt minden egyes kockázat esetében tényleges költségekre kell átszámítani.
Ha például az alábbi Mátrixban a kockázatra feltüntetett 0,40-es hatáskategória “20-40%-os költségnövekedést” jelent, és ha a kockázat bekövetkezése által leginkább érintett tevékenységek becsült összköltsége 20 000 dollár, akkor a “hatás” pénzben kifejezve 4 000 és 8 000 dollár között van, vagy
átlagosan 6 000 dollár.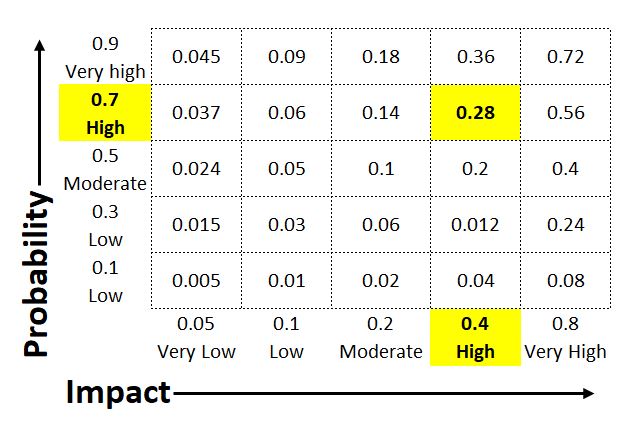

Ezt a 6 000 dolláros összeget ezután meg kell szorozni a kockázat bekövetkezésének valószínűségével a várható pénzbeli érték egyenlet segítségével:
EMV = P x I
EMV = 0.7 x $6,000 = $4,200
Döntésfa
AzEMV-t gyakran használják a döntési fáknál, és a várható érték vagy a várható pénzérték fogalmának ─ a kitettséghez hasonló fogalom ─ ismerete szükséges hozzá.
Képzeljük el például, hogy veszünk egy sorsjegyet 1,00 dollárért. Két lehetséges nyeremény van: 100,00 és 10 dollár. 00
- A szelvények 5%-a 100 dollárt fizet.
- 0%-a 10 dollárt fizet.
- A maradék 97,5% nem fizet semmit!
| Díj értéke | Nyerési valószínűség | átlagos hozam |
| $ 100.00 | 0.005 | $ 0.50 |
| $ 10.00 | 0.02 | $ 0.20 |
| $ 0 | 0.975 | $ 0 |
| Total | 1.000 | $ 0.70 |
A fent idézett példában bármelyik tét átlagos eredménye 0.70$. Ezt az “átlagos eredményt” nevezzük várható értéknek.
A várható értéket egyetlen fogadáson soha nem nyerhetjük meg, de ha sokszor megismételnénk az esélyt, akkor átlagosan minden feltett 1,00 dollár után 0,70 dollárt kapnánk.
Ezzel a technikával kapcsolatban sok jó dolog van, hiszen így megkapjuk;
- Az összes azonosított kockázat átlagos kimenetelét.
- Várható tartalékot.
- A make or buy döntések alapját.
- A történelmi adatokat szem előtt tartó döntések alapját.
Hasonlóképpen van néhány hiányossága ezeknek az eljárásoknak, mint például
- A használata csak nagyobb projektekre korlátozódik, így kis projekteknél nem használható.
- Nagymértékben támaszkodik a múltbeli adatokra és a szakértői véleményekre, így a személyes tetszés nem tetszés befolyásolhatja a projekt végeredményét.
- A téves múltbeli adatok végül hatással lesznek a projektre.
- A kockázatok számáról szóló kevesebb információ végül az egyes kockázatok nagyobb hatását eredményezi, ami nem biztos, hogy helyes.
Összefoglaló
A projekt kockázatelemzése nem fejezhető be anélkül, hogy bizonyos összeget tartalékként ne helyeznénk el. Projektmenedzserként mindig magabiztosnak érzi magát, ha már van egy jobb kockázatelemzés és némi tartalék a kezében.
FEATURED POSTS
Primavera P6 letöltése
Mi az a PMP?
Stakeholder Engagement
Munkamegosztási struktúra
Projektmenedzsment
Gantt diagram
Tervezőmérnök
Csapatfejlesztés
Tuckman




