円柱の表面積 – 解説と例題
円柱の表面積の話題に入る前に、円柱についておさらいしておきましょう。 幾何学では、円柱は互いに平行な2つの円形の底面と曲面を持つ立体図形です。
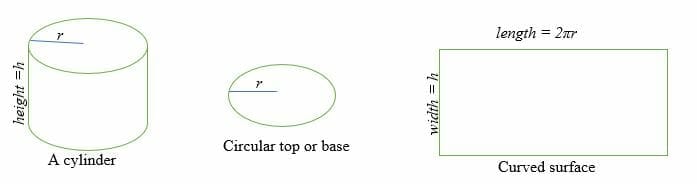
円柱の表面積の求め方
円柱の表面積は、平行で合同な2つの円形の面と曲面部分の和になります。
この記事では、円柱の総表面積と側面表面積の求め方について説明します。
円柱の表面積を計算するには、底面積(B)と曲面面積(CSA)を求める必要があります。 したがって、円柱の表面積または全表面は、底面積を2倍したものと曲面面積の和に等しくなります。
円柱の曲面は、長さが2πr、幅がhの長方形に等しく、
ここでr=円形面の半径、h=円柱の高さです。
曲面の面積=長方形の面積=l×w=πdh
底面積B=円の面積=πr2
円柱の面積の公式
円柱の総表面積の公式は、次のように示される。
円柱の全面積=2πr2+2πrh
TSA=2πr2+2πrh
ここで2πr2は上下の円面の面積、2πrhは曲面の面積を表します。
右辺から2πrを共通因子とすると、
TSA = 2πr (h + r) …………………………………………………………………………………………………… (円柱の表面積の公式)
円柱の表面積に関する例題を解いてみましょう。
例題1
半径5cm、高さ7cmの円柱の総表面積を求めよ。
解答
式より、TSA = 2πr (h + r)
= 2 x 3.14 x 5(7 + 5)
= 31.4 x 12
= 376.8 cm2
例2
総面積が 2136.56 平方フィートで、高さが 3 フィートであるシリンダの半径を求めます
解答
与えられる:
TSA = 2136.56平方フィート、
高さが 3フィート。56平方フィート
高さ、h = 3フィート
しかし、TSA = 2πr (h + r)
2136.56 =2 x 3.14 x r (3 + r)
2136.56 = 6.28r (3 + r)
右辺の乗法の分配性により、
2136.56 = 18.84r + 6.28r2
各項を 6.28
340 で割ると、以下のようになる。22 = 3r + r2
r2 + 3r – 340.22 = 0 ……(二次方程式)
二次方程式を使って方程式を解くと、
r = 17
したがって、シリンダの半径は17フィートであることがわかります。
例題3
円筒形の容器を塗装する費用は1cm2あたり0.04ドルである。 半径50cm、高さ80cmの容器20個の塗装費用を求めよ。
解答
容器20個の合計表面積を計算せよ。
TSA = 2πr (h + r)
= 2 x 3.14 x 50 (80 + 50)
= 314 x 130
= 40820 cm2
コンテナ20個の総面積= 40,820 cm2 x 20
= 816,400 cm2
塗装費= 816,400 cm2 x $0.1
= 1,000 cm2
= 1,500 cm204 per cm2
= $32,656.
したがって、20個の容器を塗装する費用は$32,656.
例4
円柱の総面積が2552 in2、半径が14 inであれば、その高さを求めよ。
解答
与えられた:
TSA = 2552 in2
半径、r = 14 in.
しかし、TSA = 2πr (h + r)
2552 = 2 x 3.半径は2 x 2です。14×14 (14+h)
2552 = 87.92(14+h)
両辺を87.92で割ると、
29.1 となる。026 = 14 + h
両辺を14で引くと
h = 15
したがって、円柱の高さは15インチです。
円柱の横表面積
前述のように、円柱の曲面面積はいわゆる横表面積と呼ばれるものです。 簡単に言うと、円柱の底面と底面(円形)の面積を除いた表面積が円柱の側面面積です。
LSA = 2πrh
例5
直径56 cm、高さ20 cmの円柱の側面面積を求めます。
解答
より:
直径=56cm、したがって半径r=56/2=28cm
高さh=20cm
式より、
LSA=2πrh
=2×3.14×28×20
= 3516.8cm2
したがって、円柱の横の表面積は3516.8cm2
例6
円柱の横の表面積は144フィート2です。 円柱の半径を7フィートとすると、円柱の高さを求めよ。
解答
与えられた;
LSA = 144 ft2
半径、r = 7 ft




