合成分割法
合成分割は、多項式の分割の中で最も「楽しい」方法だと言わざるを得ません。 多項式除法に比べ、答えに到達するまでのステップ数が少ないからです。 このレッスンでは、合成除算を使用して多項式をうまく分割するための基本的な手順に慣れていただくために、5つの例題について説明します。
- 除数は必ずx – Ⓐの形にします。
合成分割を使った多項式の割り算の例
例1: 下の多項式を割ってみましょう。
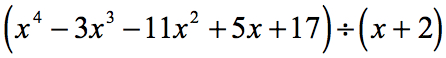
与えられた問題をもう一度確認し、必要なら調整しましょう。
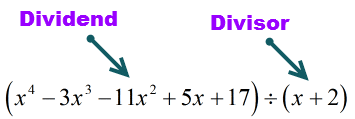
配当(分けるもの)は指数が小さい順なので標準形になっていますね。 これはいい!
除数は
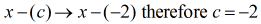
と書き換える必要がある。この時点で、配当の係数を抽出し、それを上に並べれば合成除算の設定ができるようになったのだ。
左側に直接、c = – 2 の値を「箱」の中に入れます。
最後に、配当の係数のすぐ下に水平線を構築します。
手順:
1.配当の係数を抽出します。 水平線の下に最初の係数を落とす。
2. その落とした数字に「箱」の中の数字をかける。 その積が何であれ、2番目の係数のすぐ下の横線の上に置く。
3. 数字の列を足し、その和を横線の真下に置く。
下のアニメーションの解を参照:
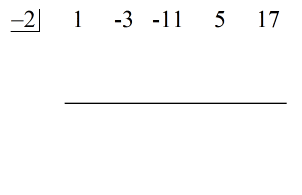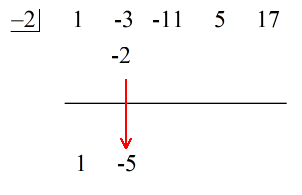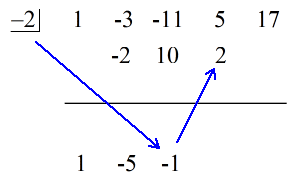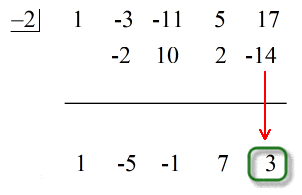
横線下の最後の数字は常に余りになる!
4…
4. この問題の余りは3です。
では、最終的な答えをどのように示すかですが、
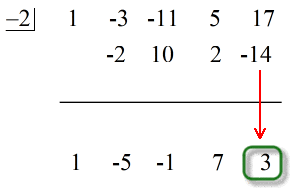
- 最終答えを
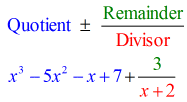
最終(余り)を除く水平線以下の数字は商の係数に注目しましょう。
さらに言えば、商の変数の指数はすべて1ずつ減っている。
例題2: 多項式を割りなさい。
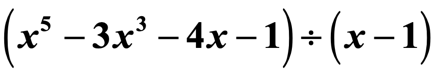
これはひっかけ問題ではありません。 商には変数xのすべての指数がないことに注意してください。
{x^4}と{x^2}が抜けていることがわかりますね。 変数xの累乗の係数をすべて含めるには、元の問題をこのように書き直せばよいのです。 足りないxには0を付けます。 また、除数を x – (c) と表すと、c の値、つまり c = + 1 がはっきりとわかります。
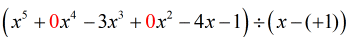
ここから、数字を設定して処理を続けることができます。
手順:
1. 最初の係数を横線より下に落とす。
2. その落とした数字に「箱」の中の数字を掛ける。 その積が何であれ、2番目の係数のすぐ下の横線の上に置く。
3. 数字の列を足し、合計を横線の真下に置く。
4. 追加する列がなくなるまでこの作業を繰り返し行う。
下のアニメーションの解答を参照してください。
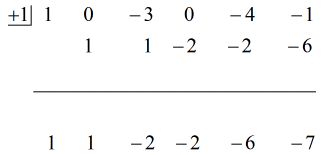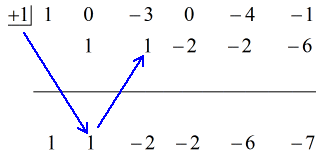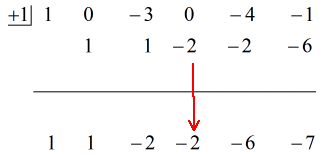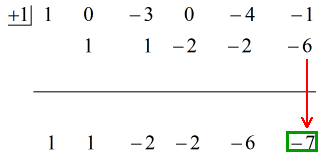
そこで、最後の答えを
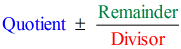
とすると
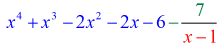
例3:下の多項式を割る。
left( { – 2{x^4} + x} \right) ╱️{x – 3}╱️
だんだん面白くなってきたぞ! 商は確かにひどいですね、たくさん抜けてますから。 x^3}と{x^2}といういくつかのxが足りないだけでなく、定数もなくなっています。
「新しくなった」問題は次のようになります:
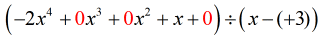
ここからは、いつものように手順を進めます:
Steps:1. 横線の下に最初の係数を落とす。
2. その落とした数値に「箱」の中の数値を掛ける。 その積が何であれ、2番目の係数のすぐ下の横線の上に置く。
3. 数字の列を足し、合計を横線の真下に置く。
4. 追加する列がなくなるまでこの作業を繰り返し行う。
下のアニメーションをご覧ください。
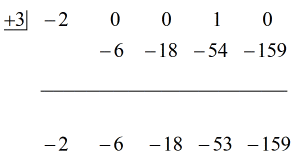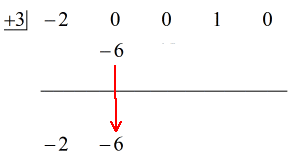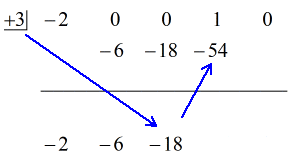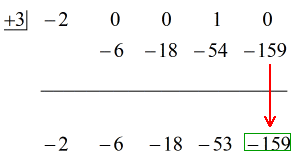
さて、この場合の最後の答えは
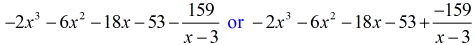
二通りの方法で書くことができます。 一つ目は、マイナスや引き算の記号を使って、余りがマイナスであることを示す方法です。 もうひとつは、+記号を使いながら、分子にマイナス記号をつける方法です。 どちらも同じ意味です!
例題4:下の多項式を割る
◇left( { – {x^5} + 1} \right) ◇left( {x + 1} \right)
この問題で落ち込まないでくださいね。 この問題は実はとても簡単です。特に、すでにいくつかの例題を経験した今となっては、なおさらです。 常に「足りない部分を埋める」ことを忘れないでくださいね。
配当を見て、足りない部分が {x^4}, {x^3}, {x^2}, そして x であることに同意してください。
合成除算が可能な元の問題を書き直すと…
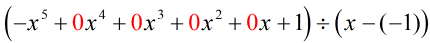
足りない x をゼロで埋めて、明示的に c = -1 を解く。
手順:
1.xをゼロにする。 最初の係数を水平線より下に落とす。
2. その落とした数値に「箱」の中の数値を掛ける。 その積が何であれ、2番目の係数のすぐ下の横線の上に置く。
3. 数字の列を足して、その和を横線の真下に置く。
4.
下のアニメーションの解答をご覧ください:
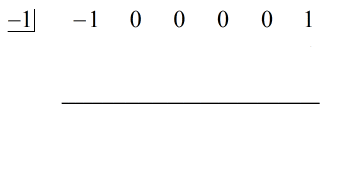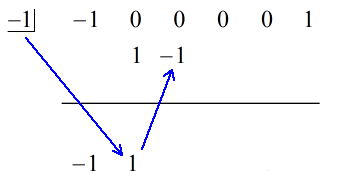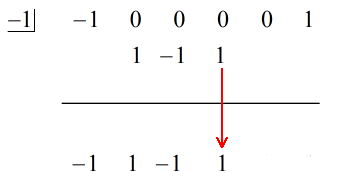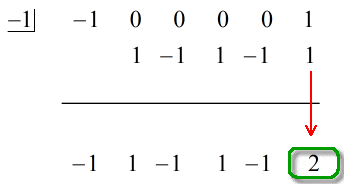
水平線の下の最後の数字は常に余りになります。 それを忘れないでください。 この場合、余りは2になります。
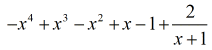
例5:多項式を2項で割る。
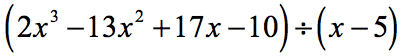
この例では、余りをゼロとすることになります。 そのとき、除数は配当の因数になる。 言い換えれば、除数は配当を均等に割るということです。
問題を調べてみると、足りない成分はないようです。 xの累乗はすべて説明され、定数もあります。 それは素晴らしいことです。
ステップ:
1.この問題は、実際に合成除算の準備ができています。 最初の係数を横線の下に落とします。
2. その落とした数値に「箱」の中の数値をかけます。 その積が何であれ、2番目の係数のすぐ下の横線の上に置く。
3. 数字の列を足し、その和を横線の真下に置く。
4. 追加する列がなくなるまでこの作業を繰り返し行う。
下のアニメーションの解答を参照してください。
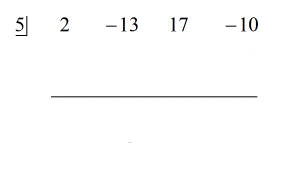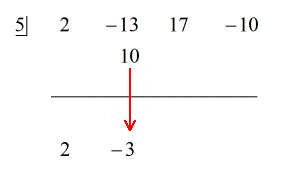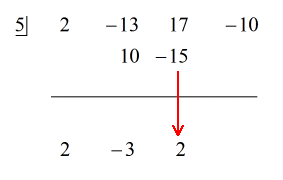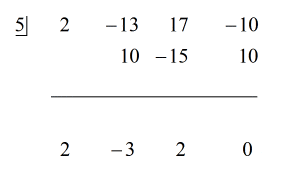
余りは0になるので。 これは、除数 x – 5 が配当の因数であることを意味します
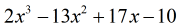
したがって
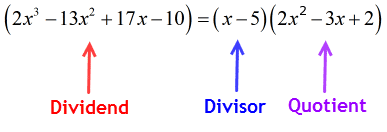
ワークシートで練習
こちらもご覧ください。
多項式の足し算と引き算
長割法による多項式の割り算
FOIL法による二項整数の掛け算
多項式の掛け算
に興味がある方




