四角形の性質-長方形、正方形、平行四辺形、ひし形、台形
ユークリッド幾何学では、四角形とは内角の合計が360°である4辺形の平面図形とされています。 四辺形という言葉は、ラテン語で4と辺を意味する「quadri」と「latus」に由来しています。 したがって、四辺形を他の多角形と区別するためには、四辺形の性質を把握することが重要です。
それでは、四辺形の性質とは何でしょうか。
- 四角形は4つの辺を持つ閉じた形であること
- 四角形の内角はすべて360°になる
この記事では、5種類の四角形についてアイデアを得て、四角形の性質について知ることができます。
記事内ではこのようなことが書かれています。
- 四角形の種類
- 長方形
- 長方形の性質
- 長方形の公式
- 正方形
- 長方形の性質 正方形の性質
- 正方形の公式
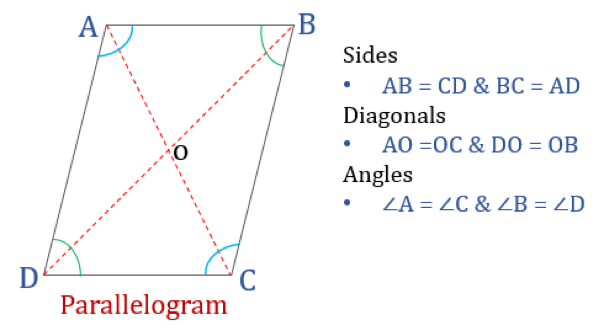
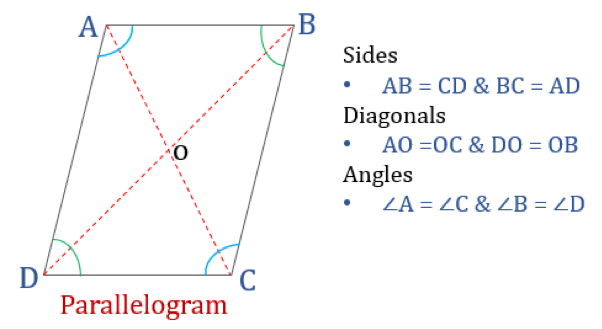
- 平行四辺形
- 平行四辺形の性質
- 平行四辺形の公式
- 平行四辺形の公式 ひし形
- ひし形の性質
- ひし形の公式
- 台形/台形
- 台形の性質
- 台形の公式
- 四角形の性質
- 重要な四角形の公式
- 四角形の質問
四角形の性質を説明したビデオです。
下の図は四角形ABCDとその内角の和を表しています。 したがって、∠A + ∠B + ∠C + ∠D = 360°
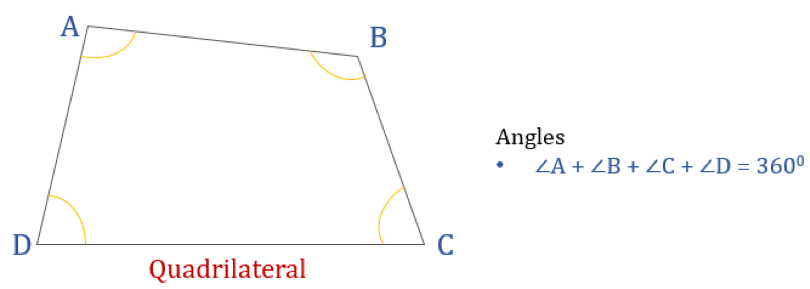
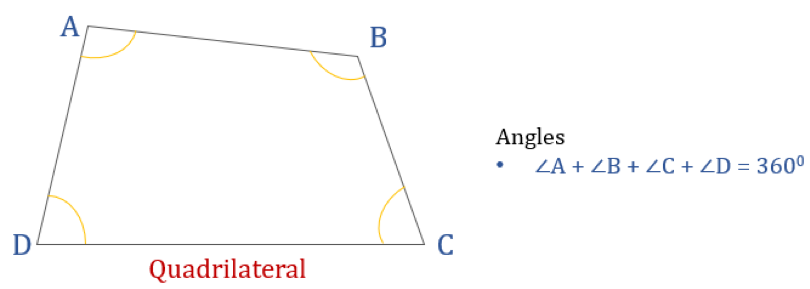
四角形の種類
四角形はその形状から5種類に分けられます。
- 長方形
- 正方形
- 平行四辺形
- ひし形
- 台形
これらの5つの四辺形について詳しく説明しましょう。
ここで、今回学習する5つの四角形すべての性質を応用する方法を学ぶことができる問題を出題します。
長方形
長方形は4つの直角を持つ四角形です。 したがって、長方形の角はすべて等しくなります(360°/4=90°)。 さらに、長方形の対向する辺は平行で等しく、対角線は互いに二等分する。
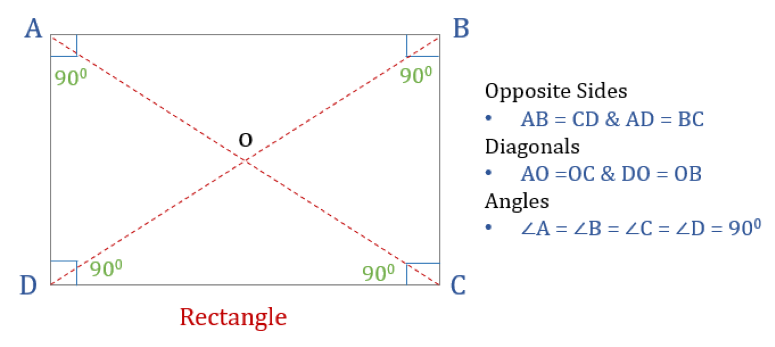
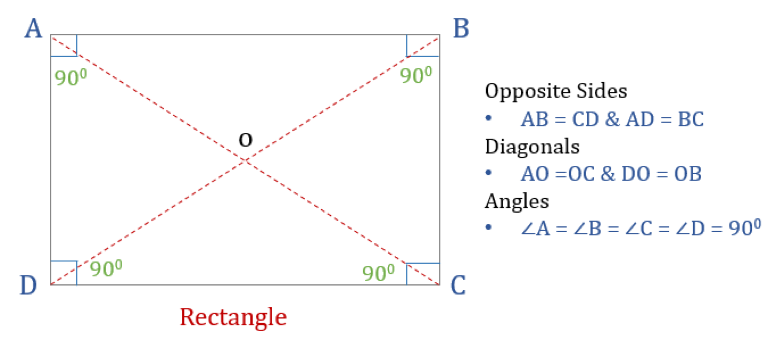
長方形の性質
長方形は三つの性質を持っています。
- 長方形の角はすべて90°
- 長方形の対辺は等しく平行
- 長方形の対角線は互いに2等分
長方形の公式 – 長方形の面積と周囲
長方形の長さをL、幅をBとすると、以下の通りです。
- 長方形の面積=長さ×幅またはL×B
- 長方形の周囲=2×(L+B)
これらの練習問題で、長方形の性質を固めます
四角
四角は4辺と角が同じである四角形の一種である。 また、その辺と角の両方が等しいので、正四角形である。 長方形と同じように、正方形は90°の角度を4つずつ持っています。 477>
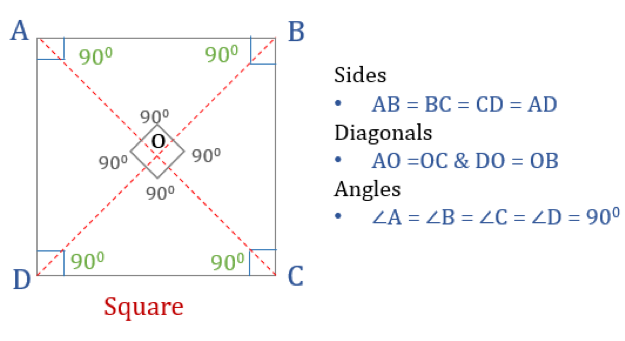
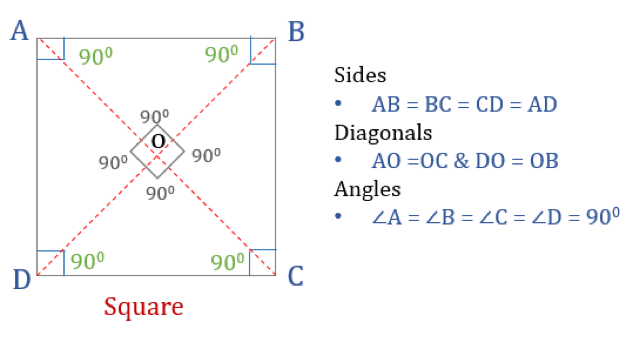
正方形の性質
四角形が正方形であるためには、ある性質を持っていなければならない。 ここでは正方形の3つの性質を紹介します。
- 正方形のすべての角は90°
- 正方形のすべての辺は等しく、互いに平行
- 対角は互いに垂直に二等分
正方形の公式 – 正方形の面積と周囲
正方形の辺を ‘a’ としたとき。
- 正方形の面積=a×a=a²
- 正方形の周囲=2×(a+a)=4a
これらの練習問題で正方形の性質を固めましょう
GMATでQ50-51を得点すれば700点以上取れるので、GMATで得点することに役立ちます。 GMATでQ50-51を取るために、私たちの無料の準備資料でGMATの準備を始めませんか? また、「GMAT」受験のための準備として、「GMAT」受験のための準備として、「GMAT」受験のための準備として、「GMAT」受験のための準備として、「GMAT」受験のための準備として、「GMAT」受験のための準備として、「Q35」を3週間で 「Q50」まで向上させたキャリー ローから学んでください。 したがって、2組の平行な辺を持つ。 さらに、平行四辺形の対角は等しく、対角線は互いに2等分します。
平行四辺形の性質
以下の性質を満たす四辺形を平行四辺形と呼ぶことにします。 平行四辺形には4つの性質がある。
- 向かい合った角が等しい
- 向かい合った辺が等しく平行
- 対角線が互いに二等分
- 隣り合った角の和が180°
Parallelogram Formula – Area and perimeter of a parallelogram
Parallelogramの長さをlとすると, その辺の長さは’le’ とする, 幅をb、高さをhとする。
- 平行四辺形の周囲=2×(l+b)
- 平行四辺形の面積=l×h
これらの練習問題で固めることができるのは、以下の通りです。 平行四辺形の性質
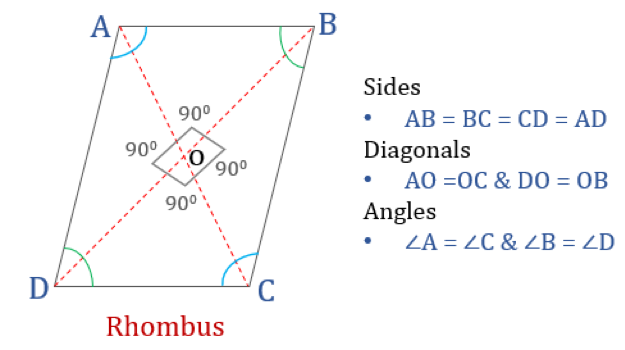
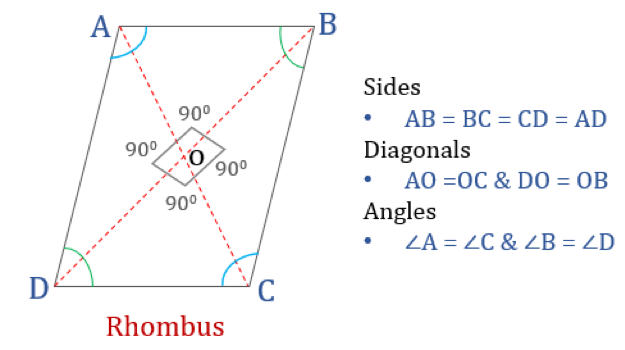
ひし形
ひし形は、4辺の長さが等しく、向かい合った辺が互いに平行な四角形である。 ただし、角は90°に等しくない。 直角のひし形は正方形になります。 ひし形の別名は、トランプのダイヤのスーツに似ていることから「ダイヤ」。
ひし形の性質
ひし形は次の四つの性質を持つ四角形である。
- 反対側の角は等しい
- すべての辺は等しく、。 対辺は互いに平行
- 対角線は互いに垂直に二等分
- 隣り合う角の和は180°
ひし形の公式-ひし形の面積と周囲
ひし形の辺をa とすると。 ひし形の周囲=4a
ひし形の対角線の長さをd1、d2とすると、ひし形の面積=½×d1×d2
これらの練習問題では、ひし形の面積を求めることができます。 477>
Trapezium
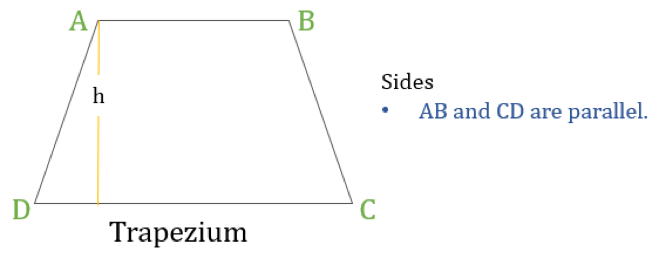
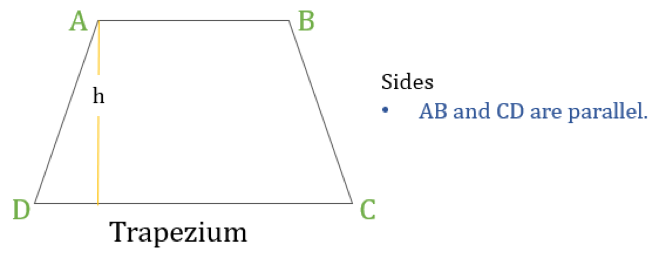
台形(アメリカではTrapezoidと呼ばれる)とは、平行な辺を1組だけ持つ四角形のことである。 平行な辺は「底辺」と呼ばれ、他の2つの辺は「脚」または「側辺」と呼ばれる。
台形の性質
台形は次の一つの性質を持つ四角形である。
- 対向する辺の1組だけが互いに平行
台形の公式-台形の面積と周囲
台形の高さをhとすると(上の図のように)、次のようになります。
- 台形の周囲=すべての辺の長さの和=AB+BC+CD+DA
- 台形の面積=½×(平行辺の長さの和)×h=½×(AB+CD)×h
これらは、「台形の面積と周囲」です。 練習問題で台形の性質を固める
四角形の性質
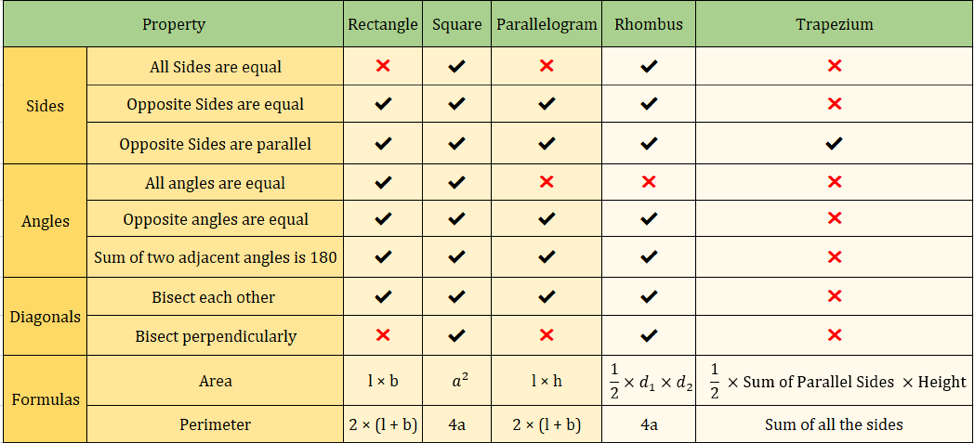
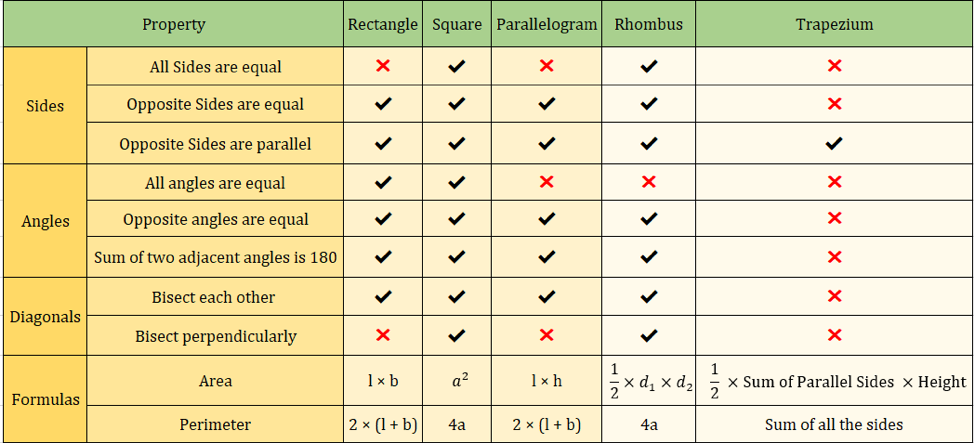
下の表は、これまで学習した四角形の性質をまとめたものです。
四角形の性質 長方形 正方形 平行四辺形 ひし形 Trapezium
全ての面が等しい ✖ ✔ ✖ ✔ 対極性 辺が等しい ✔ ✔ ✔ ✖ 対辺が平行 ✔ ✖✔ ✔ ✔ すべての角度が等しい ✔ ✖ ✔<8796 ✖ ✖ 反対の角は等しい ✔ ✔ ✔ ✖ の3つ。
隣り合う2つの角の和は180 ✔ ✔ ✖ 二等分する ✔ ✔ ✖ 垂直に二等分する ✔ ✔ ✔ ✔ ⚪︎ ✖✖✖✖✖ ✖✖✖ ✖✖✖✖ ✖✖✖
✔✖ ✖ ✖ 下の画像も四辺形の性質をまとめています。
重要な四角形の公式
下の表は異なる種類の四角形の面積と周囲に関する公式を要約したものです。
四角形の公式 長方形 正方形 平行四辺形。 菱形 台形 面積 l × b a² l × h 1/5 × d1 × d2 ½ ×(平行な辺の和)×高さ 周囲長 2 ×(l+b) となる。
4a 2 × (l + b) 4a 全辺の和 さらに読みます。
- 円の性質|円の公式-面積と周囲長
- 数の性質-偶数&奇数|素数|HCF & LCM
- 三角形の性質-定義|種類|三角形
- 三角形の定義-定義|種類|HCF
- 円の性質|円の公式-周長
- 円の性質|円の公式|周長2860 分類
- 線と角-性質とその応用
四角形問題
以下のサンプル問題で、四角形の性質の応用練習をしましょう。
Question 1
アダムは長さ10m、幅15mの長方形の庭に柵を作りたいと考えています。 庭全体を囲うには何メートルのフェンスを買えばよいでしょうか。
- 20m
- 25m
- 30m
- 40m
- 50m
Solution
ステップ1:与えられた
- Adam には長方形の庭園があります。
- 長さは10m、幅は15mである。
- 彼はその周りにフェンスを作りたいと思っている。
ステップ2:
- 庭全体にフェンスを作るために必要な長さを求める。
ステップ3:アプローチと作業
フェンスは庭の外側の辺にしか作れません。
- そこで、必要なフェンスの総長=庭のすべての辺の長さの合計
- 庭は長方形なので、すべての辺の長さの合計とは庭の周囲以外の何ものでもありません。
- 周囲=2×(10+15)=50メートル
したがって、フェンスの必要な長さは50メートルです。
質問:2
スティーブは自分の部屋の長方形の壁の一つを塗りたいと考えています。 壁を塗るための費用は1平方メートルあたり1.5ドルである。 壁の長さが25メートル、幅が18メートルだとすると、壁を塗るのにかかる総費用はいくらでしょうか。
- $ 300
- $ 350
- $ 450
- $ 600
- $ 675
Solution
ステップ1:与えられた
- Steve は自分の部屋の壁を一つ塗装したいと思います。
- 壁の長さは25m、幅は18mです。
- 壁を塗るコストは1平方メートルあたり1.5ドルです。
ステップ2:求める
- 壁を塗るための総コスト
ステップ3:アプローチと作業
- 壁はその全域を塗る。
- だから、平方メートルで壁の総面積を求め、壁の1平方メートルをペイントするためのコストを掛けると、我々は総コストができます。
- 壁の面積=縦×横= 25メートル×18メートル= 450平方メートル
- 壁を塗るための総コスト= 450 × $1.5 = $675
したがって、正解は選択肢Eです。
今までに、四角形の種類、性質、公式、およびこれらの概念を適用して四角形に関する問題を解く方法を学んでいただけたと思います。 GMATの幾何の問題を解くには、四角形の応用が重要です。 GMATを受験される方は、こちらから無料でアクセスできる高品質な学習教材でサポートいたします。
数学に関する記事はこちら:
- Improve accuracy in Math questions on Polygons
- Geometry Questions – Most Common Mistakes|GMAT Quant Prep
GMAT を受ける予定がありましたら、準備として高品質のオンラインコンテンツへのアクセスを提供することが可能です。 gmatclubで最もレビューの多いGMAT対策会社で、1950以上のレビューがあります。
まずは無料体験をして、ご自身で判断されてはいかがでしょうか?
何か疑問があれば、[email protected]。