確率論入門。 解答付き記事と動画!

admin 0 Comments Articles

確率論入門。 解答付き記事と動画!

Share on

サイコロを振る、駐車場を探す、トランプで勝つなど、ある出来事が起こる確率を求めたい場面はいくつかあります。 確率を求める方法を知りたい場合は、まず、どのような質問があるのかを把握する必要があります。 例えば、ある事象が起こる確率を求める方法と、グループのメンバーが同じものを選ぶ確率を求める方法は異なります。

ある種の確率は、サイコロの転がる確率やカードの山から選ぶ確率を求めるように、簡単に特定できるものです。

二項定理を使った問題も特定しやすい。 この種の実験では、事象の可能な結果は「成功」か「失敗」のみで、「はい/いいえ」「頭/尻尾」「黒/白」のようなものです。

  • グループや委員会から人を選ぶ。
  • グループが同じものを選ぶ確率。

事象

単純な事象が起こる確率を見つけたいですか？ たとえば、雨が降ること、あるいは、ダウンタウンで駐車スペースを見つけること、などでしょうか。
Probability of a simple event happening.を参照してください。
一方、その逆の場合は、
How to find out the probability of an event not happening.を参照してください。 例えば、ゲームの日に駐車スペースを見つける確率や、ブラックフライデーに特定の人気のあるおもちゃを見つける確率などでしょうか。 もしそうなら、チェックしてみてください。

  • 別の事象が与えられた場合の、ある事象の確率。
  • 一緒に発生する 2 つの事象。

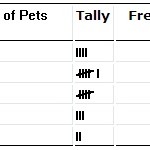
度数分布表。

Frequency Distributions

扱うべき度数分布を持っていますか? あるいは、与えられたデータで度数分布表が作れますか？ 例えば、ある特徴を持ったアイテムがx個あったとします。

確率入門：ハウツー記事とビデオ

  1. 並べ替えと組合せ: 問題の解き方
  2. 確率の問題。 簡単に解ける！
  3. aとbの確率
  4. 総確率の法則
  5. ベイズの定理の問題:
  6. 事前確率（非情報的確率、共役確率を含む）…
  7. データから確率分布を作る方法…
  8. グループや委員からある人を選ぶ確率の求め方…
  9. ベイズの定理の問題：簡単な解決方法(1)確率を求めない…
  10. 確率を求めない方法（2）確率分布を作るにはどうすればよいか？
  11. ある事象が起こらない確率を求める方法
  12. 確率頻度分布
  13. 単純な事象が起こる確率を求める方法
  14. ランダム事象
  15. ある確率が起こる確率が起こる確率が起こる確率が起こる確率を求める方法

    16. ある確率が起こらない確率が起こらない確率

  16. ある確率が起こる確率が起こる確率
  17. グループのメンバーが同じものを選ぶ確率の求め方
  18. 2つの従属事象が同時に起こる確率の求め方
  19. 別の事象があるとき、その事象が起こる確率の求め方
  20. ある確率の求め方
  21. グループメンバーから選ばれる確率がある確率を求め方
  22. 確率木（決定木）を使って確率を計算する方法
  23. デックからカードを引く確率を求める方法
  24. 互いに排他的なイベントかどうかを判断する方法
  25. 従属イベントと独立イベントの違いを識別する方法
  26. Probability.Odent (確率論的な確率)の使用法

    27. Probability.Odent (確率的な確率的な確率)の使用法 Probability.Odent(Probable) サイコロを振る.

  27. ベン図の描き方.
  28. オイラー図の作り方.
  29. 5の選択3：組み合わせを解く方法.
  30. 基本数原理の使い方.
  31. 離散確率変数に対する期待値の求め方.

Probability Introduction to Probability.（英語）: 定義

  • 公理的確率
  • ベンフォードの法則
  • 二項実験とは何か
  • 確率の定義
  • 確率の定義
  • 確率の定義
  • 基礎率と基礎率の誤り
  • ブリアスコア
  • 集合的網羅性
  • 組み合わせとは？
  • 相補的事象＜6118>
  • 条件付き期待値＜6118>
  • 条件付き相対頻度とは何か＜6118>
  • 条件付き相対頻度は何ですか？
  • 可算加算性
  • 空集合
  • エピステミック確率
  • 事象空間.
  • 実験的確率とは
  • 限定分布.
  • 限定分布.
  • 実験的確率とは
  • 限定確率分布はどのような分布か
  • 最尤推定
  • メモリーレス特性
  • モンテカルロ法
  • モンティホール問題
  • Mutually Exclusive Eventとは何か
  • Mutually Inclusive Eventsとは何か
  • Mutual Likelihoodとは何か
  • Maximationは何か
  • Mutually Likelihoodは何か
  • Maximationは何か
  • 相互独立と一対一独立
  • 乗法ルールとは
  • ナッシュ均衡
  • 非空集合
  • 正規確率練習問題.
  • 正規確率プロットとは
  • 目的確率
  • オッズ比とは
  • 予測分析
  • 確率分布表とは確率的確率分布
  • 確率的確率分布表とは

    • 予測的な確率計算 確率的確率分布表とは 確率的な確率計算

  • 確率の測定
  • 確率空間とは
  • 確率ベクトル
  • サンプル空間とは
  • 確率モデル
  • 主観的確率とは確率ベクトル

    • 確率ベクトル確率空間とは＜＜9118>確率ベクトル＜9111>確率ベクトル＜6118>確率ベクトル＜＜6118>確率モデル＜9111

  • 理論的確率とは何ですか？
  • Urn Modelとは何ですか？

計算機.

  • オンライン順列計算機と組み合わせ計算機.

Probability Formulas / Probability Rules

学生が最も嫌がることのひとつに、確率・統計において数式がないことが挙げられます。 いくつかの定番があり、必ず知っておくべき表記もあります。

Probability Range
0 ≤ P(A) ≤ 1
これは、ある事象の確率が0から100%の間（10進数にすると0と1）であることを示すものです。 この法則は、事象の確率を足したりかけたりするときに覚えておくとよいでしょう。

相補事象のルール
P(AC) + P(A) = 1
相補事象は、コインをはじくように、結果が 2 つしかないときに発生します。 サイコロを振って6が出るかどうかも補集合であり、6が出るか（1/6の確率）、出ないか（5/6の確率）の2つしかない。 この式は、
p(A) + p(A’) = 1
のように書くこともでき、代数的に並べ替えると、
p (A’) = 1 – p (A) のようになります。 個人的にはA’が好きで、”not A “と呼んでいます。 Aではない」確率は、「補数」（ある出来事が起こるか、起こらないか）よりも理解しやすいと思います。

加算則
P(A∪B) = P(A) + P(B) – P(A∩B)
ここで∪は和、∩は交です。
これが言いたいことは（英語では！）、「Aではない」確率は「補数」よりも理解しやすいと思います。イベント A またはイベント B (または両方が同時に) 起こる確率は:

  • イベント A が単独で起こる確率、
  • さらにイベント B が単独で起こる確率、
  • さらに両方のイベントが同時に起こる確率を加えたものです。

相互に排他的な事象がある場合、P(A∩B)は起こりえない（事象が同時に起こらない）ので、式は次のようになる。
P(A∪B) = P(A)+P(B)- 0 = P(A)+P(B)

Disjoint Events
Event A and B are disjoint if:
P(A∩B) = 0
This is just another way of saying the event are mutually exclusive.この式は、イベントとイベントが互いに分離していることを表しています。


関連した式に P((A∪B)c) または等価に ((A∪B)’) があります。 これは英語では “not the union” と言います。 これを解くには、和を求め、その結果を1から遠ざける（事象が起こるか起こらないかの確率を足すと1になるはずだから）

条件付き確率
P(A|B) = P(A∩B) / P(B)
記号の意味は「～とすれば」である。 つまり、事象Aが起こったと仮定したときに、事象Bが起こる確率を表しています。 この式の使い方の例は、条件付き確率を参照してください。

ベイズの公式
P(A|B) = P(B|A) – P(A) / P(B)
ベイズの定理は、少しニュアンスが違いますが、条件付き確率を計算する方法です。 一言で言えば、テストに関する情報が与えられたときに、ある事象が実際に起こる確率を求めるものです。 例えば、健康診断で陽性だった場合、あなたが癌である確率はどのくらいか（答えは、あなたが思っているよりずっと低い）。 いくつかの例については、こちらをご覧ください。 ベイズの定理の例と事後分布／事後確率を参照してください。

独立事象
事象AとBは、一方が他方の確率に影響を与えないなら、独立である。
P(A∩B) = P(A) – P(B).
この式は乗法から導かれ、P(A∩B) = P(A) * P(B|A) である。 324>

Some Notes on Probability Rules

統計は偶然と大まかな計算であり、絶対や「正しい答え」ではない。 ギャラップ社の世論調査を調べてみてください-彼らは「正しい答え」を持っていると90%以上確信していることはめったにありません。 確率を計算するのに使えるテクニックはある（2つの確率を掛け合わせたり、足したりする）。 しかし、二項分布表と上記の公式（現実にはあまり使われませんが）以外には、簡単に適用できる確率の公式はないのです。 そのため、小学校で習うような論理学に戻らなければなりません（覚えていますか？）

確率の公式の3つのルール：

  1. ルールはない（まあ、上に挙げたものを除いてはほとんどない）
  2. 式ではなく、論理を使う。

今朝届いた、確率に関する質問です。

「チーズパフのパックに入っている6枚の野球カードを集めようとしている場合、それらが均等に分布していると仮定すると、6枚すべて揃うまでに何パックのチーズパフを購入すると思いますか」

この問題を解くステップ1は、表で答えを調べることができないことを理解することです。

カード1：あなたは8歳に戻り、チーズパフを1袋買えるだけのお金を持って店に入りました。 あなたは野球のカードを5枚全部集めたいと願っていますが、まだ1枚も持っていません。 袋を買って、欲しいカードが手に入る確率はどのくらいでしょうか。

もちろん、答えは100％です。 最初の袋を買って、その中に欲しいカードが入っている確率は100％です。

カードその2：今度は少し難しいです。 あなたはカード#2を手に入れるために店に戻ります。 しかし、すでにカード#1、ミッキー・マントルを手に入れました。 しかし、1/5の確率でミッキー・マントルが手に入るかもしれません（したがって、4/5の確率で手に入らないかもしれません）。 2番目のカードを手に入れるために、チーズパフを何袋買わなければならないかが、比率の問題になる。 頭の中で考えることもできますが、数学的にモデル化するのであれば、方程式を設定する必要があります。

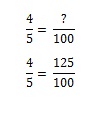
100%にするには1.25袋購入する必要があります。

カード3：確率はより厳しくなり始めます。 3枚目の野球カードを手に入れる確率は60%で、3枚目を手に入れるには1.667袋購入する必要があります。

Card# 4:少し悲惨な確率になり始めました。 4枚目のカードを手に入れる確率は40％で、3枚目を手に入れるには2.5袋買わなければなりません。

Card# 5:確率はあなたに不利です。


つまり、あなたが購入しなければならない袋の総量は、
1 + 1.25 + 1.667 + 2.5 + 5
と同じです。 (ここで、ちょっとした理屈が登場します）。 チーズパフを1.25袋買うことはできないので、切り上げなければなりません。 式は次のようになります：
1 + 2 + 2 + 3 + 5 = 13袋

式に関する重要なポイント：絶対的なものは何もないことを忘れないでください。 チーズパフを13袋購入し、カードが均等に配分されていると仮定すれば、5枚すべてのカードを手に入れることができると、私はそれなりに確信しています。 しかし…確率は偶然の産物であり、10回連続で同じカードが出るのはあなたの運が悪いだけかもしれません（子供の頃、そんなことがあったのを覚えているのですが…）。 それは、企業はあなたにできるだけ多くの袋を買ってもらいたいので、確率を自分たちに有利になるようにしようとするのです。 たとえカードが均等に配られたとしても、会社は1番、2番、3番のカードが入った袋をある店に出荷し（したがって、半分以上のカードを集めるように仕向ける）、4番と5番を別の店に出荷することができるのです。

メーカーが自分たちに有利になるような他の方法は何か考えられるか？

Probability of a Group Choosing the Same Thing

確率の質問は異なるタイプに分けることができる。 グループが同じものを選択する確率を求める質問では、グループのランダムなメンバー（委員会のような小さなものから、米国の人口のような大きなものまであります）の行動を考慮することになります。
これらの確率の問題は、グループを与え、そのグループ内の特定の数のランダムなメンバーのイベントが発生する確率を計算するように求めます。

同じものを選ぶグループの確率：ステップ

サンプル問題：ブックフェアに200人がいる。 そのうち159人が少なくとも1冊は本を買うだろう。 もしあなたが入口から出てきた無作為の5人を調査したら、彼らが全員少なくとも1冊の本を買ったことになる確率はどのくらいか。

グループが少なくとも1冊の本を買う確率はどのくらいか。

ステップ1：問題のデータを分数に変換する。 たとえば、「200人中159人」というのは、次のように変換できます。 159/200.

Step 2: 分数に自分自身を掛けます。 ランダムな項目（つまり人）がいくつ選ばれても繰り返す。

159/200 x 159/200 x 159/200 x 159/200 x 159/200 = 0.3176
これが「同じものを選ぶ確率」の求め方です！

159/200 x 159/200 x 159/200 x 159/200 x 5952
このように、同じものを選ぶグループの確立は、次のようになります。

ヒント：分数を10進数に変換してからかけると簡単な場合があります。 この場合、159/200 = 0.795。

統計のヘルプやヒントは、YouTube チャンネルでご覧ください！

統計のヘルプやヒントは、YouTube チャンネルでご覧ください。 よくある問題を動画でご紹介しています。 また、基本的な棒グラフの作成から複雑なデータ分析問題の解決まで、統計学>でExcelを使用するためのビデオも用意されています。 “確率入門。 解答付きの記事とビデオ!” StatisticsHowTo.comより。 私たちのための初歩的な統計学! https://www.statisticshowto.com/probability-and-statistics/probability-main-index/

————————————————————–

Need help with a homework or test question? Chegg Studyでは、その分野の専門家からステップバイステップの解決策を得ることができます。 Cheggのチューターとの最初の30分間は無料です!

コメントを残す

メールアドレスが公開されることはありません。