Entropy – The Pillar of Thermodynamics and Information Theory
Entropy は、熱力学と情報理論における多くの重要なアイデアのバックボーンを形成する、曖昧だが強力な用語である。 エントロピーは、19世紀に物理学者によって初めて認識され、産業革命の革命的な技術の多くに指針として作用した。 しかし、この言葉は、数学者クロード・シャノンの画期的な著作「通信の数学的理論」に登場し、情報化時代の火付け役ともなった。 では、1 つの用語が、約1 世紀を隔てて、関連しながらも異種の分野における 2 つのブレークスルーをもたらしたのはなぜでしょうか。
まず、物理科学においてエントロピーがどのように解釈されているかから見ていきましょう。 熱力学の第一法則は、いかなる閉じた系においても、エネルギーは生成も破壊もできないと定めています。 第二法則はエントロピーの法則とも呼ばれ、開放系では熱力学的平衡に達するために、エネルギーは常に濃度の高いところから低いところへ流れる、と定めています。 では、実際にはどうなのだろうか。 例えば、コーヒーの入ったマグカップは時間とともに冷たくなり、飲み物の中の氷は溶けていきます。また、火の中に置かれた道具は、炎のエネルギーが鉄の分子に伝わり加熱されますが、それを取り除くとエネルギーが新しい周囲の環境に分配され、冷却されることを意味します。

エントロピーという言葉は、与えられたシステムにおける無秩序の状態を指しているのです。
エントロピーは、システム外部の力によって作用されない限り、一方向(平衡方向)にしか動かず、その場合でも、生物システムのような外部の力は、一時的にしかエントロピー プロセスの逆転に成功せず、最終的には(死によって)容認します。 どんな植物や動物も、エントロピーのプロセスを相殺し、環境から利用可能で秩序あるエネルギーを集め、栄養分を取り除いた廃棄物を放出することで生存している複雑なエネルギー系である。 しかし、生命システムにおけるエネルギーの処理能力は、最終的にその物理的構造を劣化させ、生物は分解して死ぬ(最終的な目標である生殖を完了したことが望まれる)。 もはや生きていないエネルギー体は分解され、周囲の環境に放散され、熱力学的平衡になります。
理論的には、エントロピーは、宇宙の熱的死(自由エネルギーが存在しない究極の状態)をもたらすと初めてその順調な歩みを止めることができます。 地球上と宇宙空間のすべてが最終的に膨張し、爆発し、死に、宇宙という最大の閉鎖系に自由エネルギーを均等に分配することになるのです。 このように、エントロピーは生物物理学の最小スケールと最大スケールの両方で作用するため、重力に似た普遍的な法則です。
経済は生物であり、洗濯機ではない
エントロピーは経済にも適用される。 周囲の環境から利用可能なエネルギーを獲得し、それを無秩序なエネルギーに変換することによる生物体内のエントロピー過程は、生物集団にも当てはまる。 社会は、低エントロピーのエネルギー源をストックとフローの2つの形態で摂取している。 ストックには、希土類鉱物や化石燃料など、数千年にわたる複雑で長期的な地球プロセスによって形成された地上の堆積物が含まれる。 フローは、風力、水力、太陽エネルギーなど、再生可能なエネルギー源とされるものから発生し、太陽エネルギーの間接的な延長としてバイオマスも含まれる。 それぞれの資源が持つ性質から、ストックは量に限りがあるのに対し、フローは速度と量の両方に限りがある。 文明は、生物と同様に新陳代謝を行う。

産業革命は経済の主要なエネルギー投入量を初めてフローから地上のストックに移行させた。 馬の鋤と風帆というフローに依存した労働形態が、化石燃料に依存する機械化農業と蒸気駆動の船舶に取って代わられたのである。 私たちは、何百万年もかけて化石化した眠っている太陽エネルギーを利用して、文明を生物学的な地球の流れの束縛から解放し、人口と GDP の猛烈な成長を実現しました。
このシフトによる否定できない経済および材料上の利点にもかかわらず、エントロピー・プロセスを早め、気候系の無秩序さを増加するという副作用が生じました。 経済プロセスを通じて、エネルギーの総量は(太陽エネルギーを除いて)変化しないが、生産プロセスに必要な鉱物の採掘と化石燃料の消費は、エネルギーを秩序から無秩序へと移行させる質的な変化を特徴づけている。 エントロピーがなければ、大気中の二酸化炭素を石炭の塊に戻すことは物理的に可能であり、タイヤが舗装路で劣化して失われたゴム粒子を捕捉して再構成することも可能である。

結局のところ、我々の経済はモノとエネルギーを使っているのである。 私たちの価値の表象である貨幣が経済内を無限に循環していても、それが表象する物理的な財は、エントロピーの法則に従うのです。 現在の経済システムは、無限に成長する生物のようなものである。 心臓は血液を送り出し、私たちを生かしているが、その力は時間とともに私たちの細胞を摩耗させる。
では、エントロピーはデータサイエンスにどのように適用されるのでしょうか。
さて、エントロピーがどのようにエネルギーを指すかを見てきましたが、コミュニケーションと情報理論にどのように適用されるかを見てみましょう。 Jimmy Soni と Rob Goodman による Claude Shannon の伝記「A Mind at Play」からの抜粋は、エントロピーの起源に関する素晴らしい逸話だと思います。 これを何と呼べばいいのか。 フォン・ノイマンは即座にこう答えた。「情報は『エントロピー』を減らすと言いなさい」。 一つは、物理学的にしっかりした良い言葉だからだ。 さらに重要なことは、誰もエントロピーの本当の意味を知らないということだ。だから、議論では常に自分が有利になる」。”

Shannon のエントロピーに関する定義を扱う前に、彼の情報についての定義を分解してみるとよいでしょう。 シャノンの理論の基本的な考え方は、伝達されたメッセージの情報的価値は、メッセージの内容がどの程度驚くべきものであるかに依存するというものです。 このことを実際に示す好例が、言語における文字の頻度の利用である。 確率的には、文字のインスタンスを1つの事象とすると、与えられたすべての事象の最も可能性の高い結果はこの確率分布に従う:
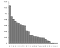
文字数が多いほどメッセージに不確実性がないことになる。 しかし、それは文字の希少性にもよる。 たとえば、次のメッセージは 1 と 2 のどちらがより情報的なパンチがあるか。
_AT
オプション「1」には比較的高い確率の 2 文字が含まれており、足りない文字を埋めることによってあらゆる種類の単語を綴ることができます。 「Bat”, “Cat”, “Hat”, “Fat”, “Sat “などです。 選択肢2には、比較的とらえどころのない文字「H」が含まれており、「Hat」や「Hit」など、いくつかの単語の選択肢が残っていますが、選択肢1ほどではありません。 したがって、選択肢2は不確実性をより大きく減らすので、より多くの情報を伝えることになる。
つまり、情報が解決された不確実性であるとすれば、エントロピーは解決されるべき不確実性でなければならない。 ある事象の希少性、つまり「驚き」がその情報量を決定する(スクラブルをやったことがある人なら、「Q」という文字を引いたら選択肢がどれだけ限定されるか分かるだろう)。 情報を伝達するたびに、全体のエントロピー、無秩序、不確実性、その他何と呼ぼうとも、それに比例した量や割合で減少していくのです。 では、この比例量とは何でしょうか?
シャノンは、各可能なデータ値に関連する情報エントロピーの尺度は、その値に対する確率質量関数の負の対数であると計算した。
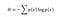
エントロピーは、起こりうる結果を確率関数とし、ランダムイベントの結果を特定することによって伝えられる情報の期待量を測定します。 これは、ダイスを投げることは、コインを投げるよりもエントロピーが高いことを意味します。なぜなら、ダイスを投げる各結果 (⅙) は、表または裏 (½) になるよりも確率が小さいからです。 この関係をグラフで見てみると、次のようになります:

表という結果を伝えることによって、裏が発生しなかったことを知ることができる。
機械学習では、エントロピーの数学的解釈は、多くのアルゴリズムの情報利得メトリックを計算するために使用されます。 たとえば決定木は、サンプルをサブセットに繰り返し分割するために、特徴または独立変数としても知られる多くの異なる属性のうちの 1 つを選択します。 各分割時に、アルゴリズムはサンプルを分割する属性を1つ選択し、すべてのサブセットが純粋になるまで、言い換えれば、サブセット内の個々のサンプルが同じ分類または目標値を共有するまでこれを続ける。
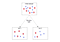
サンプル サブセットの純度を測定するには、アルゴリズムは任意のノードで分割する機能をオフラインで選択できる定量測定器が必要です。 ここで、エントロピーの出番となります。 各ステップで、アルゴリズムはどの属性が最も高い情報利得を示すかを計算し、次に分割を決定する。 また、分割前と分割後の不確実性の減少を計算し、減少していれば、分割を維持し、次のステップに進む。 減少していない場合は、純化に達したと判断し、休息する。 このように、熱力学と情報理論の間にリンクがあるか?
エントロピーは、コーヒーカップから空気中に不可避的に流れるように、決定木を通して不可避的に流れる。 エネルギーでは、熱力学的平衡に向かって行進し、情報理論では、純粋さに向かって行進します。
その核心は、エントロピーに対するエネルギーの解釈と情報理論の解釈は、物理の基本法則という同じ点に収束することです。 通信にはエネルギーが必要であり、エネルギーを使うには通信が必要である。 シャノンによれば、情報のエントロピー値は、メッセージの平均的な長さをどれだけ短くできるか、つまり、送信時に情報を失うことなくどれだけ圧縮できるかという絶対的な制限を与えているのである。 半導体、懐中電灯、モールス信号で鍋をたたくには人間のエネルギーが必要であり、私たちの通信は常に最も効率的な伝達手段を追求する。
エネルギーでは、消費する量とその効率を制限することによって、エントロピーを最小化しようとしている。 私たちの目標は、秩序あるエネルギー源を見つけ、身体へのエントロピーの影響に抵抗することです。 通信分野では、情報を見つけ、不確実性を減らすことでエントロピーを最小化します。 狩猟採集民が、ライオンに食われることを警告するために、言語を使って他の人とコミュニケーションをとることで、1.ライオンの居場所(情報エントロピー)と2.ライオンに食われる過程(エネルギーエントロピー)の不確実性を減らすことができるのです。 このように、伝えるという行為は、あらゆる事象の確率空間を縮小し、より効率的かつ効果的に行動することを可能にするのである。 この強力な法則がデジタルと物理の領域でどのように作用しているかの本質を理解することは、熱力学と情報化時代のつながりを理解する上で重要な鍵となります
。




