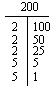Numbers in Their Prime
すべての整数は、0と1という特殊なケースを除いて、素数と合成のどちらかに分類される。 ここでは、素数と合成数の違いを見てみましょう。 素数には、1とその数自身というちょうど2つの因子があります。 割り切れる法則(次のセクションで取り上げます)を知っていれば、1〜100までの素数を決めるのは比較的簡単な作業です。 以下は25までの素数です。
2, 3, 5, 7, 11, 13, 17, 19, 23
数学者は800万桁近い素数を見つけていますが、存在するすべての素数を見つけるパターンは存在しません。 3689>
合成数には2つ以上の因子があるが、無限の因子はない。 すべての偶数(2を除く)は、すべて2で割ることができるので、合成数である。
ゼロは素数でも合成数でもない。 0 の任意の倍数は 0 に等しいので、0 の積の因子は無限に存在する。 合成数は有限個の因子を持たなければならない。
1も素数でも合成数でもない。 1の積を得るには1×1を掛けるしかないが、重複する因子は1度しか数えられないので、1には因子が1つしかない。 (3689>
典型的なテスト問題では、リストからどの数が素数(または合成数、あるいはどちらでもない数)であるかを特定させます。
- 33
- 45
- 41
- 51
Reveal Answer
正解はC。41は素数、他の数字は合成数である。 51は3×17からきているので注意しましょう。
Cool Rules
可分法則とは、割り算を少なくするための道具です。 3689>
可分性の規則は、ある数字が他の数字で割り切れるかどうかを知るための近道です。 この法則は、2~10の数による割り算をカバーしており、100までの数を確認することができます。 表中の数字をクリックしてください。
| Divisibility Rules | ||
|---|---|---|
| 2 | 3 | 4 |
| 5 | 6 | 7 |
| 8 | 9 | 10 |
質問
次の数の中で3で割り切れないものはどれでしょう?
- 4,873
- 7,521
- 12,642
- 25,308
Reveal Answer
The correct answer is A. Fast way to do this problem is using the divisibility rule; add the digit of each number looking for the one not a multiple of three.これは、それぞれの数字を足して3の倍数にならないものを探すルールです。 遅い方法は、それぞれの割り算の問題を行うことです。電卓でも、この方法は時間がかかります!
Prime Factorization: Tと木
これも中学生のときから考えていなかったかもしれない話題です。 算数の基本定理では、すべての合成数は素数の一意な積に分解できるとされています。
素因数分解とは、与えられた合成数の素数積を求める処理です。 素因数分解はそれ自体も便利ですが、その応用として、この先で取り上げる分数に関するものが多くあります。
ある数の素因数分解は、頭の中で見つけることができるかも知れません。 例えば、12は2×2×3や22×3です。(素因数分解はしばしば指数で表されます)
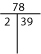
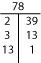
もし、素因数分解を頭の中で見つけることができなければ、Factor-TかFactor Treeを試してみてください。