Skewness – クイックイントロダクション、例、および公式
Skewness は、変数がどの程度
非対称に分布しているかを示す数値です。
- 正(右)偏り度の例
- 負(左)偏り度の例
- 人口偏り度-公式と計算
- 標本偏り度-公式と計算
- 標本偏り度-正と負の偏り度の例
- 人口偏り度-正と負の偏り度の例
- SPSS における歪度
- Skewness – データ分析への影響
- (標準)正規分布、
- t分布、
- (p=0.5とした場合の二項分布)などがあります。000…
母集団の歪度-公式と計算
1つまたは複数の変数の歪度を計算したい場合は、いくつかのソフトウェアに計算を任せればよいでしょう。 しかし、-念のため-とりあえず数式を列挙しておきます。
データに全人口が含まれている場合、母集団の歪度を次のように計算します。
$Population;skewness = \Sigma}{X_i – \mu}{sigma}biggl)^3cdot}{1}{N}$
where- (X_i) is each individual score.各個人のスコアを表す。
- (\mu) は母平均、
- (\sigma) は母標準偏差、
- (N**) は母数である。
この式を使った計算例は下のGoogleシートをご覧ください。
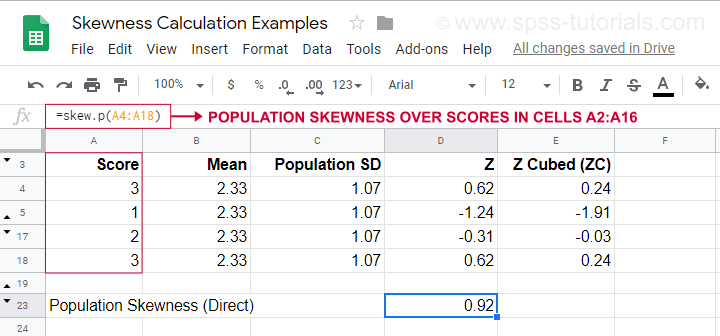
また”.P “は “population “の意味で、=SKEW.P(…)で直接母数の歪度を得る方法が示されています。 これで、手計算の結果を確認することができました。 残念なことに、SPSSもJASPも母集団の歪度を計算することはできず、標本の歪度に限定されています。
Sample Skewness – Formula and Calculation
データが母集団からの単純無作為標本の場合は、
$$Sample.P.P.を使用します。歪度 = \frac{NcdotSigma(X_i – \overline{X})^3}{S^3(N – 1)(N – 2)}$
where- (\overline{X}) is the sample mean;
- (Sante) is the sample-standard-deviation,
- (Nante) is the sample size.
計算例をこのグーグルシート(下図)に示します。
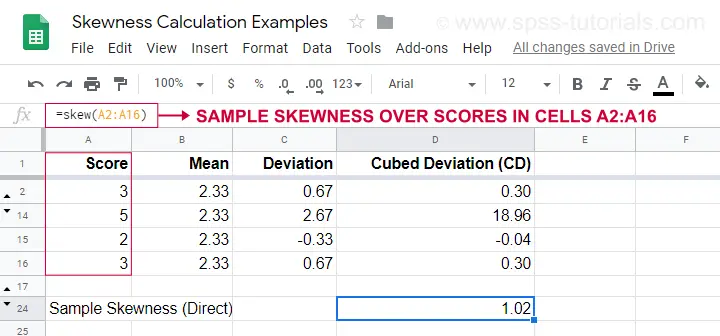
標本の歪度を簡単に求めるには、=SKEW(…)を使用すると手計算の結果を確認できます。
SPSS
まず最初に、SPSSにおける「歪度」は常に標本歪度を指します。これは、データが母集団全体ではなく、標本を保持していると静かに仮定しているのです。 それを得るための多くのオプションがあります。 構文と出力がクリーンでシンプルなので、私のお気に入りはMEANS経由です。 平均、標準偏差、中央値などを含む非常に完全な表が、means v1 to v5
/cells count min max mean median stddev skew kurt から実行されます。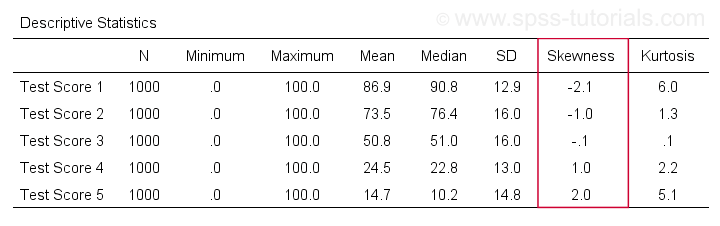
Skewness – Implications for Data Analysis
Many analyses – ANOVA, t-tests, regression and others – requires the normality assumption: variables should be normally distributed in the population.その結果は以下のように表示されます。 正規分布は歪度=0であるため、あるサンプルデータでかなりの歪度を観察すると、正規性の仮定に違反していることを示唆します。
このような正規性の違反は、N > 20または25といった大きなサンプルサイズでは問題ありません。 この場合、ほとんどの検定がこのような違反に対してロバストです。 これは中心極限定理によるものです。 しかし、歪度はしばしば大きな標準偏差を伴います。 しかし、歪度は大きな標準偏差を伴うことが多く、その結果、標準誤差が大きくなり、統計的検出力が低くなることがあります。 このように、歪度が大きいと、ある効果を示すために、ある帰無仮説を棄却する確率が低下することがあります。 この場合、ノンパラメトリック検定がより検出力を持つので、より賢明な選択となるかもしれません。正規性の違反は、例えばN < 20程度の小さなサンプルサイズでは、本当の脅威
をもたらします。 小さな標本サイズでは,多くの検定が正規性の仮定の違反に対してロバストでない. 最後になりましたが、母集団の歪度=0かどうかを調べる統計的検定がありません。これを調べる間接的な方法は、- Kolmogorov-Smirnov 正規性検定や
- Shapiro-Wilk 正規性検定などの正規性検定があります。
しかし、正規性が本当に必要な場合(サンプルサイズが小さい場合)、これらの検定の検出力は低く、正規性からの逸脱が深刻であっても統計的に有意にならない場合があります。 このように、これらは主に誤った安心感を与えてしまうのです
。
- 正と負の偏り度の例
正(右)歪度の例
ある科学者が1,000人がいくつかの心理テストに参加しました。 テスト5について、テストの得点は歪度=2.0である。 3337> 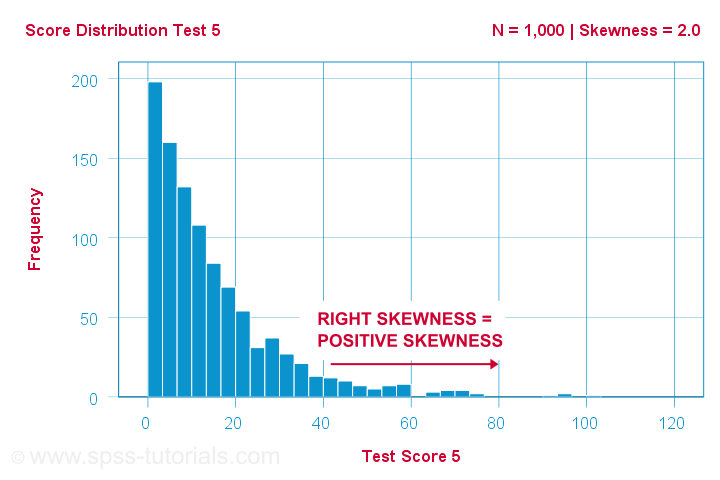
このヒストグラムは、非常に非対称な度数分布を示しています。 ほとんどの人は20点以下ですが、右の尾は90点くらいまで伸びています。 この分布は右傾化しています。
X軸に沿って右に移動すると、0点から20点、40点と進みます。 つまり、グラフの右側に行くほど、点数は正になるわけです。 したがって、右の歪度は正の歪度であり、歪度>0を意味します。この最初の例は、グラフの右上に示すように、歪度=2.0です。 3337>
負の(左)歪度の例
別の変数-テスト2-のスコアは、歪度=-1.0であることがわかります。

得点の大部分は60点から100点の間くらいにあります。 しかし、左の尾はいくらか伸びています。 つまり、この分布は左歪みです。
右:左へ、左へ。 x軸を左にたどると、よりマイナスのスコアに向かう。 これがleft skewnessが負の歪度である理由です。そして実際、これらのスコアでは、歪度=-1.0です。 その分布は左斜めになっています。 3337>
Symmetrical Distribution Implications Zero Skewness
最後に、対称な分布は歪度=0です。テスト3の得点は歪度=0.1であり、これに近いです。 これは、ほとんどの場合、いくつかの理論的な標本化分布に見られます。 例えば、




