Egenskaper hos fyrhörningar – rektangel, kvadrat, parallellogram, romb, trapets
I euklidisk geometri är en fyrhörning en fyrsidig 2D-figur vars summa av de inre vinklarna är 360°. Ordet fyrhörning kommer från de två latinska orden ”quadri” och ”latus” som betyder fyra respektive sida. Därför är det viktigt att identifiera egenskaperna hos fyrhörningar när man försöker skilja dem från andra polygoner.
Så, vilka är egenskaperna hos fyrhörningar? Det finns två egenskaper hos fyrhörningar:
- En fyrhörning ska vara en sluten form med 4 sidor
- Alla inre vinklar i en fyrhörning summerar till 360°
I den här artikeln kommer du att få en uppfattning om de 5 typerna av fyrhörningar och lära dig mer om fyrhörningarnas egenskaper.
Det här är vad du kommer att läsa i artikeln:
- Differenta typer av fyrhörningar
- Rektangel
- Rektangelns egenskaper
- Rektangelformler
- Kvadrat
- Egenskaper. egenskaper hos en kvadrat
- Formler för kvadrater
- Parallellogram
- Egenskaper hos parallellogram
- Formler för parallellogram
- Romb
- Rombens egenskaper
- Rombformler
- Trapezoid
- Trapezoidens egenskaper
- Trapezoidens egenskaper
- Trapezoidformler
- Vadrilaternas egenskaper
- Viktiga kvadrilaterala formler
- Vadrilaterala frågor
Här är en video som förklarar egenskaperna hos kvadrilateraler:
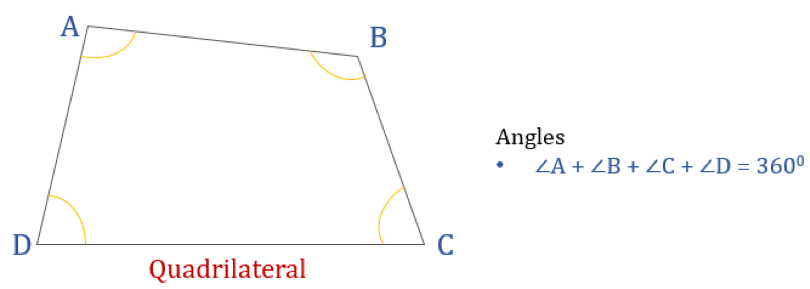
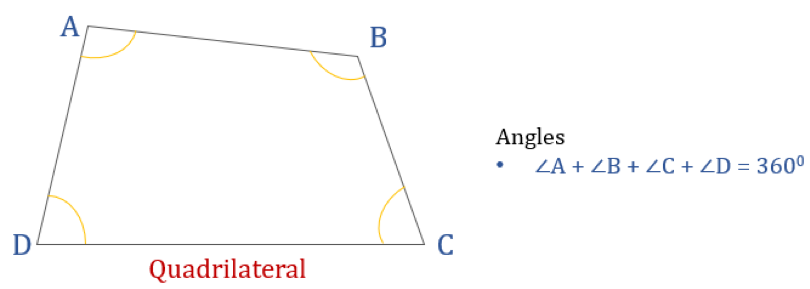
Diagrammet nedan visar en fyrhörning ABCD och summan av dess inre vinklar. Alla inre vinklar summerar till 360°.
Därmed blir ∠A + ∠B + ∠C + ∠D = 360°
Olika typer av fyrhörningar
Det finns 5 typer av fyrhörningar utifrån deras form. Dessa 5 fyrhörningar är:
- Rektangel
- Fixt
- Parallelogram
- Romb
- Trapez
Låt oss diskutera var och en av dessa 5 fyrhörningar i detalj:
Här är frågor som kommer att lära dig att tillämpa egenskaperna hos alla 5 fyrhörningar som du kommer att lära dig i den här artikeln.
Rektangel
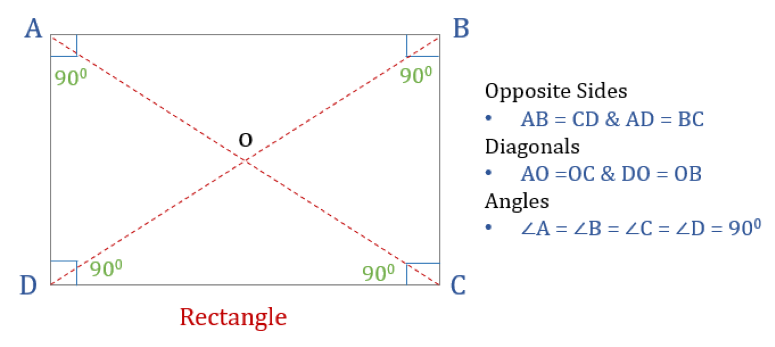
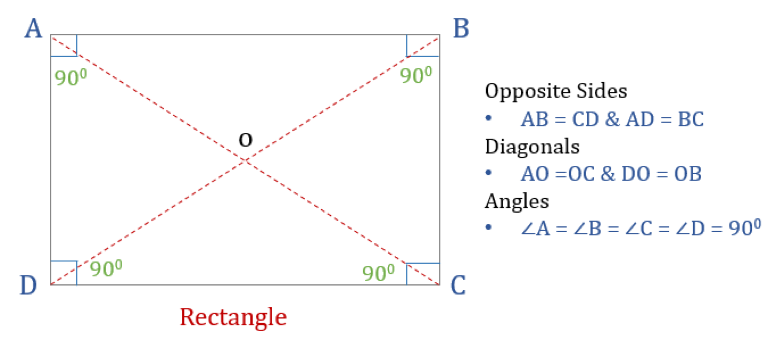
En rektangel är en fyrhörning med fyra räta vinklar. Alla vinklar i en rektangel är alltså lika stora (360°/4 = 90°). Dessutom är de motsatta sidorna i en rektangel parallella och lika stora, och diagonalerna delar varandra i två delar.
Rektangelns egenskaper
En rektangel har tre egenskaper:
- Alla vinklar i en rektangel är 90°
- De motsatta sidorna i en rektangel är lika stora och parallella
- Diagonaler i en rektangel är tvådelade
Rektangelformel – Area och omkrets i en rektangel
Om längden på rektangeln är L och bredden är B så är,
- Rektangelns area = Längd × bredd eller L × B
- Rektangelns omkrets = 2 × (L + B)
De här övningsfrågorna hjälper dig att befästa egenskaperna hos rektanglar
Fjärrhörnig
Fjärrhörnig är en fyrhörning med fyra lika stora sidor och vinklar. Det är också en regelbunden fyrhörning eftersom både dess sidor och vinklar är lika stora. Precis som en rektangel har en kvadrat fyra vinklar på 90° vardera. Den kan också ses som en rektangel vars två intilliggande sidor är lika stora.
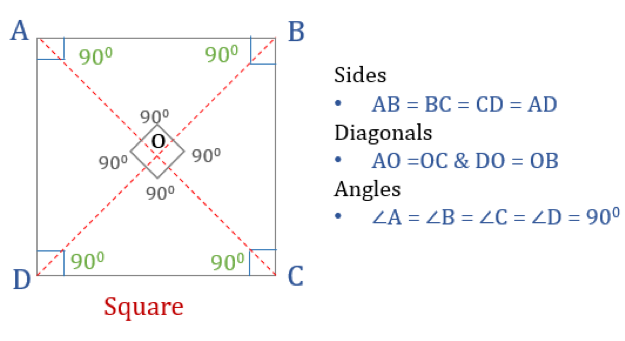
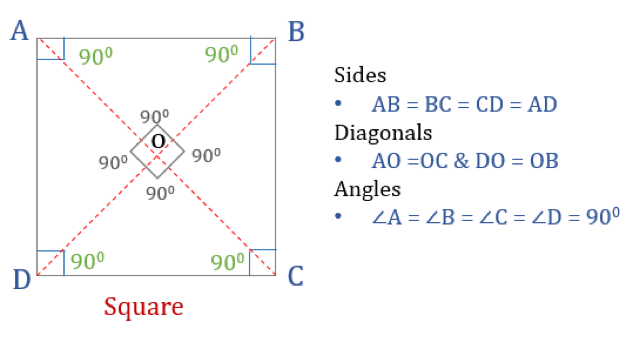
En kvadrats egenskaper
För att en fyrhörning ska vara en kvadrat måste den ha vissa egenskaper. Här är de tre egenskaperna hos kvadrater:
- Alla vinklar i en kvadrat är 90°
- Alla sidor i en kvadrat är lika stora och parallella med varandra
- Diagonaler delar varandra vinkelrätt
Förhållningssättet för kvadrater – Arean och omkretsen av en kvadrat
Om sidan i en kvadrat är ”a” så är det,
- För att få en kvadratens area = a × a = a²
- För att få en kvadratens omkrets = 2 × (a + a) = 4a
De här övningsfrågorna kommer att hjälpa dig att befästa egenskaperna hos kvadrater
Att få ett Q50-51 på GMAT hjälper dig att få ett GMAT-poäng på 700+. Varför börjar du inte förbereda dig för GMAT med våra kostnadsfria förberedelser och påbörja din resa för att få Q50-51 på GMAT. Lär dig av Carrie Law som förbättrade sig från Q35 till Q50 på 3 veckor.
Parallelogram
En parallellogram är, som namnet antyder, en enkel fyrhörning vars motsatta sidor är parallella. Den har alltså två par parallella sidor. Dessutom är de motsatta vinklarna i en parallellogram lika stora och dess diagonaler delar varandra i två delar.
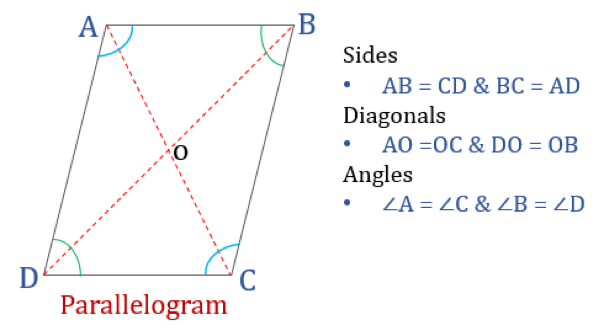
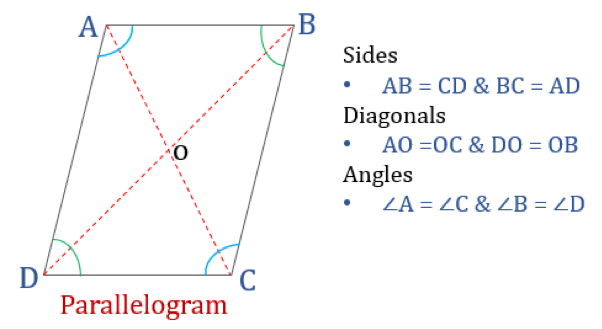
Egenskaper hos parallellogram
En fyrhörning som uppfyller nedanstående egenskaper kommer att klassificeras som en parallellogram. En parallellogram har fyra egenskaper:
- De motsatta vinklarna är lika stora
- De motsatta sidorna är lika stora och parallella
- Diagonaler delar varandra i två delar
- Summan av två intilliggande vinklar är 180°
Parallelogramformler – Arean och omkretsen av en parallellogram
Om längden på en parallellogram är ”l”, bredden är ”b” och höjden är ”h”:
- Perimeter av parallellogrammet = 2 × (l + b)
- Area av parallellogrammet = l × h
Dessa övningsfrågor hjälper dig att befästa egenskaperna hos parallellogram
Romb
En romb är en fyrhörning vars alla fyra sidor är lika långa och vars motsatta sidor är parallella med varandra. Vinklarna är dock inte lika med 90°. En romb med räta vinklar skulle bli en kvadrat. Ett annat namn för romb är ”diamant” eftersom den liknar diamantfärgen i spelkort.
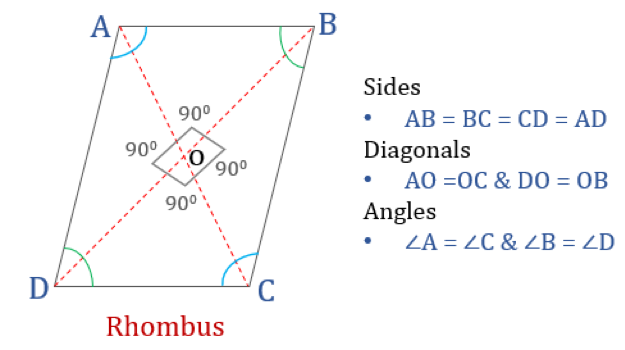
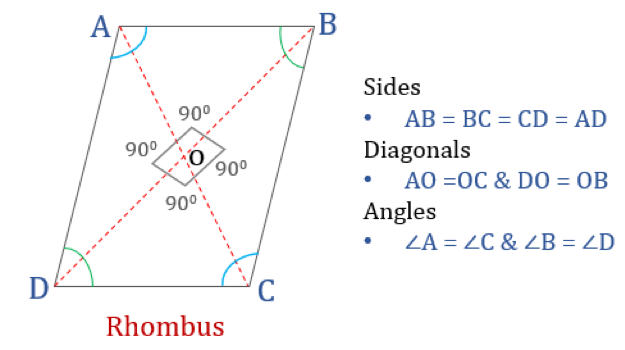
Rombens egenskaper
En romb är en fyrhörning som har följande fyra egenskaper:
- De motsatta vinklarna är lika
- Alla sidor är lika stora och, motsatta sidor är parallella med varandra
- Diagonaler delar varandra vinkelrätt
- Summan av två intilliggande vinklar är 180°
Rombformler – Arean och omkretsen av en romb
Om sidan av en romb är a så, omkretsen av en romb = 4a
Om längden av två diagonaler i romb är d1 och d2 så är arean av en romb = ½ × d1 × d2
Dessa övningsfrågor kommer att hjälpa dig att befästa egenskaperna hos romb
Trapezium
Ett trapezium (kallat Trapezoid i USA) är en fyrhörning som bara har ett par parallella sidor. De parallella sidorna kallas ”baser” och de andra två sidorna kallas ”ben” eller sidosidor.
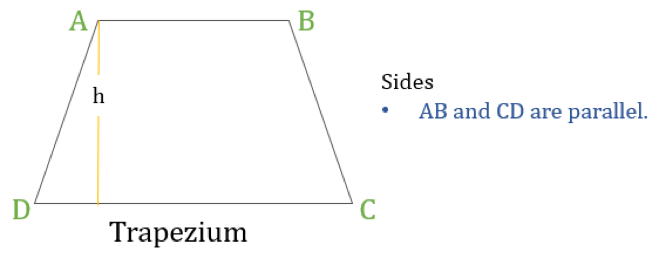
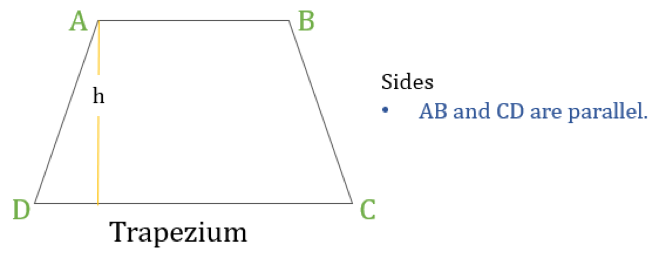
Egenskaper hos trapets
En trapets är en fyrhörning där följande en egenskap:
- Endast ett par motsatta sidor är parallella med varandra
Trapeziumformler – Area och omkrets för ett trapez
Om höjden på ett trapez är ”h” (som visas i diagrammet ovan) så gäller följande:
- Trapezets omkrets = Summan av längderna på alla sidor = AB + BC + CD + DA
- Trapezets area = ½ × (summan av längderna på parallella sidor) × h = ½ × (AB + CD) × h
Dessa övningsfrågor kommer att hjälpa dig att befästa egenskaperna hos trapetet
Vadrilaternas egenskaper
I nedanstående tabell sammanfattas alla egenskaper hos kvadrilater som vi har lärt oss hittills:
| Vadrilaternas egenskaper | Rektangel | Firkant | Parallellogram | Romb | Trapezium | ||
| Alla sidor är lika | ✖ | ✔ | ✖ | ✔ | ✖ | ||
| Motstående Sidorna är lika | ✔ | ✔ | ✔ | ✔ | ✔ | ✖ | |
| Opposit Sidorna är parallella | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ | |
| Alla vinklar är lika | ✔ | ✔ | ✖ | ✖ | ✖ | ||
| Motsatta vinklar är lika | ✔ | ✔ | ✔ | ✖ | |||
| Summan av två angränsande vinklar är 180 | ✔ | ✔ | ✔ | ✔ | ✖ | ||
| Skära på varandra | ✔ | ✔ | ✔ | ✔ | ✖ | ||
| Skära på varandra vinkelrätt | ✖ | ✔ | ✖ | ✔ | ✖ |
Under bilden nedan sammanfattas också egenskaperna hos fyrhörningar:
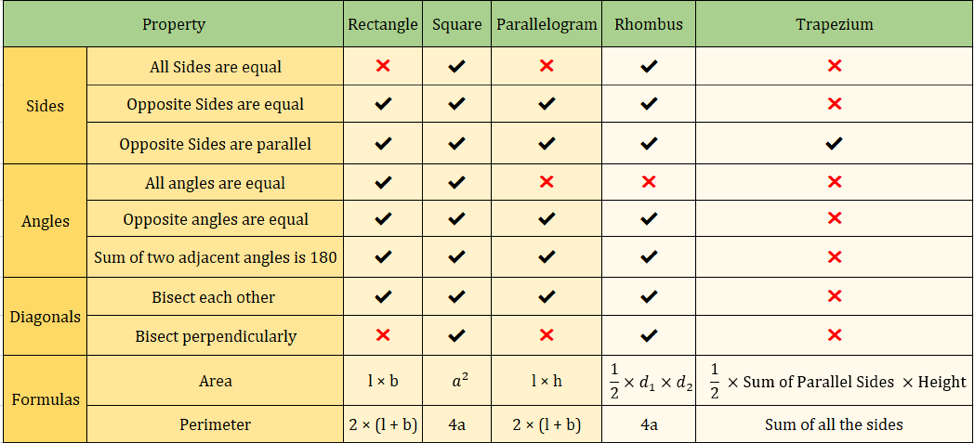
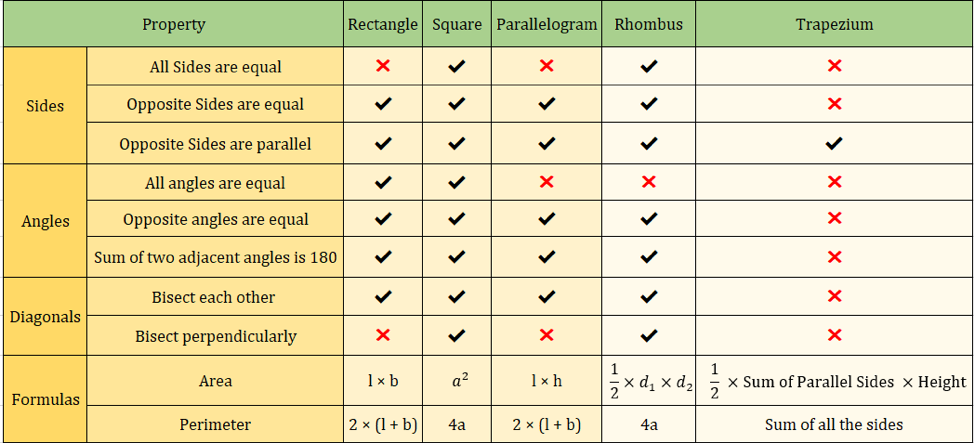
Viktiga formler för fyrhörningar
I nedanstående tabell sammanfattas formlerna för area och omkrets för olika typer av fyrhörningar:
| Formler för fyrsidiga formler | Rektangel | Firkant | Parallellogram | Romb | Trapezium |
| Area | l × b | a² | l × h | ½ × d1 × d2 | ½ × (Summan av parallella sidor) × höjd |
| Perimeter | 2 × (l + b) | 4a | 2 × (l + b) | 4a | Summan av alla sidor |
Fortsatt läsning:
- Cirkelns egenskaper | Cirkelformler – area och omkrets
- Talens egenskaper – jämna & udda | primtal | HCF & LCM
- Trianglars egenskaper – definition | typer | Klassificering
- Linjer och vinklar – egenskaper och deras tillämpning
Vadrilaterala frågor
Låt oss öva på tillämpningen av egenskaperna hos fyrhörningar på följande exempelfrågor:
Fråga 1
Adam vill bygga ett staket runt sin rektangulära trädgård som är 10 meter lång och 15 meter bred. Hur många meter av staketet ska han köpa för att stänga in hela trädgården?
- 20 meter
- 25 meter
- 30 meter
- 40 meter
- 50 meter
Lösning
Steg 1: Given
- Adam har en rektangulär trädgård.
- Den är 10 meter lång och 15 meter bred.
- Han vill bygga ett staket runt den.
Steg 2: För att hitta
- Den längd som krävs för att bygga staketet runt hela trädgården.
Steg 3: Tillvägagångssätt och utredning
Hägnet kan bara byggas runt trädgårdens yttersidor.
- Så, den totala längden på stängslet som krävs= Summan av längderna på alla trädgårdens sidor.
- Då trädgården är rektangulär är summan av längderna på alla sidor inget annat än trädgårdens omkrets.
- Perimeter = 2 × (10 + 15) = 50 meter
Därmed är den erforderliga längden på staketet 50 meter.
Därmed är alternativ E det rätta svaret.
Fråga: 2
Steve vill måla en rektangulär vägg i sitt rum. Kostnaden för att måla väggen är 1,5 dollar per kvadratmeter. Om väggen är 25 meter lång och 18 meter bred, vad är då den totala kostnaden för att måla väggen?
- $ 300
- $ 350
- $ 450
- $ 600
- $ 675
Lösning
Steg 1: Given
- Steve vill måla en vägg i sitt rum.
- Väggen är 25 meter lång och 18 meter bred.
- Kostnaden för att måla väggen är 1,5 dollar per kvadratmeter.
Steg 2: Att hitta
- Den totala kostnaden för att måla väggen.
Steg 3: Tillvägagångssätt och utredning
- En vägg målas över hela ytan.
- Så om vi hittar väggens totala area i kvadratmeter och multiplicerar den med kostnaden för att måla 1 kvadratmeter av väggen får vi fram den totala kostnaden.
- Väggens area = längd × bredd = 25 meter × 18 meter = 450 kvadratmeter
- Total kostnad för att måla väggen = 450 × 1 dollar.5 = 675 dollar
Det korrekta svaret är alltså alternativ E.
Vi hoppas att du vid det här laget har lärt dig de olika typerna av fyrhörningar, deras egenskaper och formler och hur du kan tillämpa dessa begrepp för att lösa frågor om fyrhörningar. Tillämpningen av fyrhörningar är viktig för att lösa geometrifrågor på GMAT. Om du planerar att göra GMAT kan vi hjälpa dig med högkvalitativt studiematerial som du kan få tillgång till gratis genom att registrera dig här.
Här är några fler artiklar om matematik:
- Förbättra noggrannheten i matematiska frågor om polygoner
- Geometrifrågor – de vanligaste misstagen | GMAT Quant Prep
Om du planerar att ta GMAT kan vi ge dig tillgång till högkvalitativt onlineinnehåll för att förbereda dig. Vi är det mest recenserade GMAT-förberedelseföretaget på gmatclub med mer än 1950 recensioner.
Varför tar du inte en gratis provperiod och dömer själv?
Skriv till oss på [email protected] om du har några frågor.




