En cylinders yta – Förklaring och exempel
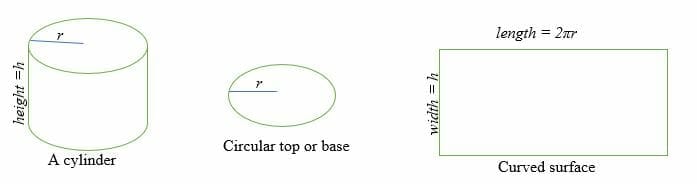
Innan vi går in på ämnet cylinders yta ska vi gå igenom en cylinder. Inom geometrin är en cylinder en tredimensionell figur med två cirkulära baser som är parallella med varandra och en krökt yta.
Hur man hittar en cylinders yta?
En cylinders yta är summan av två parallella och kongruenta cirkulära ytor och den krökta ytan.
Denna artikel kommer att diskutera hur man hittar den totala ytan och sidoytan för en cylinder.
För att beräkna ytan för en cylinder måste du hitta basytan (B) och den krökta ytan (CSA). Därför är en cylinders yta eller totala yta lika med summan av basytan gånger två och arean av den krökta ytan.
En cylinders krökta yta är lika med en rektangel vars längd är 2πr och vars bredd är h.
Varvid r = radien på den cirkulära ytan och h = höjden på cylindern.
Avdelningen av den krökta ytan = Arean av en rektangel =l x w = πdh
Basytan, B = Arean av en cirkel = πr2
Formeln för arean av en cylinder
Formeln för en cylinders totala yta ges som:
En cylinders totala yta = 2πr2 + 2πrh
TSA = 2πr2 + 2πrh
Varvid 2πr2 är den övre och nedre cirkulära ytans yta och 2πrh är den krökta ytans yta.
Om vi tar 2πr som en gemensam faktor från RHS får vi;
TSA = 2πr (h + r) ……………………………………. (Formeln för en cylinders yta)
Låt oss lösa exempelproblem som involverar en cylinders yta.
Exempel 1
Finn den totala ytan på en cylinder vars radie är 5 cm och höjd är 7 cm.
Lösning
Med hjälp av formeln,
TSA = 2πr (h + r)
= 2 x 3.14 x 5(7 + 5)
= 31,4 x 12
= 376,8 cm2
Exempel 2
Hitta radien på en cylinder vars totala yta är 2136,56 kvadratfot och höjden är 3 fot.
Lösning
Givna:
TSA = 2136.56 kvadratfot
Höjden, h = 3 fot
Men TSA = 2πr (h + r)
2136,56 =2 x 3,14 x r (3 + r)
2136,56 = 6.28r (3 + r)
Med hjälp av den distributiva egenskapen för multiplikation på RHS har vi,
2136,56 = 18,84r + 6,28r2
Divider varje term med 6,28
340.22 = 3r + r2
r2 + 3r – 340,22 = 0 ……… (en kvadratisk ekvation)
Om vi löser ekvationen med hjälp av den kvadratiska formeln får vi,
r = 17
Därmed är cylinderns radie 17 fot.
Exempel 3
Kostnaden för att måla en cylindrisk behållare är 0,04 dollar per cm2. Hitta kostnaden för att måla 20 behållare med radien 50 cm och höjden 80 cm.
Lösning
Beräkna den totala ytan för 20 behållare.
TSA = 2πr (h + r)
= 2 x 3.14 x 50 (80 + 50)
= 314 x 130
= 40820 cm2
Den totala ytan för 20 containrar = 40 820 cm2 x 20
= 816 400 cm2
Kostnaden för målning = 816 400 cm2 x 0 dollar.04 per cm2
= $32 656.
Kostnaden för att måla 20 containrar är alltså $32 656.
Exempel 4
Finn höjden på en cylinder om dess totala yta är 2552 tum2 och radien är 14 tum.
Lösning
Givet:
TSA = 2552 in2
Radius, r = 14 in.
Men, TSA = 2πr (h + r)
2552 = 2 x 3.14 x 14 (14 + h)
2552 = 87,92(14 + h)
Divider båda sidorna med 87,92 för att få,
29.026 = 14 + h
Subtrahera med 14 på båda sidor.
h = 15
Härav följer att höjden på cylindern är 15 tum.
Sidig yta av en cylinder
Som tidigare nämnts är arean av den böjda ytan av en cylinder det som kallas för den laterala ytan. Med enkla ord är en cylinders sidoarea en cylinders yta, exklusive arean av basen och botten (cirkulär yta).
Formeln ger en cylinders sidoarea;
LSA = 2πrh
Exempel 5
Finn den sidoarea av en cylinder vars diameter är 56 cm och höjd är 20 cm.
Lösning
Givet:
Diameter = 56 cm, alltså radie, r =56/2 = 28 cm
Höjd, h = 20 cm
Med hjälp av formeln,
LSA = 2πrh
= 2 x 3.14 x 28 x 20
= 3516,8 cm2.
Därmed är cylinderns sidoarea 3516,8 cm2.
Exempel 6
Den sidoarea som en cylinder har är 144 fot2. Om cylinderns radie är 7 fot, beräkna cylinderns höjd.
Lösning
Givet;
LSA = 144 ft2
Radius, r = 7 ft




