Tolkning av koefficienter för linjär regression

Tolkning av koefficienter för linjär regression

Nuförtiden finns det en uppsjö av algoritmer för maskininlärning som vi kan prova för att hitta den som passar bäst för vårt specifika problem. Vissa av algoritmerna har en tydlig tolkning, andra fungerar som en blackbox och vi kan använda metoder som LIME eller SHAP för att härleda vissa tolkningar.

I den här artikeln vill jag fokusera på tolkningen av koefficienter i den mest grundläggande regressionsmodellen, nämligen linjär regression, inklusive situationer när beroende/oberoende variabler har transformerats (i det här fallet talar jag om logtransformation).

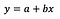
Jag utgår från att läsaren är bekant med linjär regression (om inte så finns det en hel del bra artiklar och Medium-inlägg), så jag kommer att fokusera enbart på tolkningen av koefficienter.

Den grundläggande formeln för linjär regression kan ses ovan (jag utelämnade residualerna med flit, för att hålla det enkelt och rakt på sak). I formeln betecknar y den beroende variabeln och x den oberoende variabeln. För enkelhetens skull antar vi att det rör sig om univariat regression, men principerna gäller naturligtvis även för det multivariata fallet.

För att sätta det i perspektiv, låt oss säga att vi efter att ha anpassat modellen får:

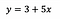
Intercept (a)

Jag kommer att dela upp tolkningen av interceptet i två fall:

x är kontinuerlig och centrerad (genom att subtrahera medelvärdet av x från varje observation blir medelvärdet av det transformerade x 0) – medelvärdet y är 3 när x är lika med provets medelvärde x är kontinuerlig, men inte centrerad – genomsnittet y är 3 när x = 0 x är kategorisk – genomsnittet y är 3 när x = 0 (denna gång anger det en kategori, mer om detta nedan)

Koefficient (b)

x är en kontinuerlig variabel

Tolkning: En ökning av x med en enhet resulterar i en ökning av genomsnittligt y med 5 enheter, alla andra variabler hålls konstanta.

x är en kategorisk variabel

Detta kräver lite mer förklaring. Låt oss säga att x beskriver kön och kan anta värden (”man”, ”kvinna”). Låt oss nu omvandla den till en dummyvariabel som tar värdena 0 för män och 1 för kvinnor.

Tolkning: genomsnittligt y är högre med 5 enheter för kvinnor än för män, alla andra variabler hålls konstanta.

lognivåmodell

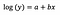
Typiskt sett använder vi logtransformationen för att dra utstående data från en positivt snedfördelad fördelning närmare huvuddelen av datan, för att göra variabeln normalfördelad. Vid linjär regression är en ytterligare fördel med att använda logtransformationen tolkningsbar.

Som tidigare, låt oss säga att formeln nedan presenterar koefficienterna för den anpassade modellen.

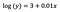
Intercept (a)

Tolkningen är likadan som i vaniljfallet (nivånivå), dock måste vi ta exponenten för interceptet för tolkning exp(3) = 20,09. Skillnaden är att detta värde står för det geometriska medelvärdet av y (till skillnad från det aritmetiska medelvärdet i fallet med nivånivåmodellen).

Koefficient (b)

Principerna liknar återigen nivånivåmodellen när det gäller tolkning av kategoriska/numeriska variabler. Analogt med interceptet måste vi ta koefficientens exponent: exp(b) = exp(0,01) = 1,01. Detta innebär att en ökning av x med en enhet orsakar en ökning av det genomsnittliga (geometriska) y med 1 %, alla andra variabler hålls konstanta.

Två saker som är värda att nämna här:

• Det finns en tumregel när det gäller att tolka koefficienter i en sådan modell. Om abs(b) < 0,15 är det ganska säkert att säga att när b = 0,1 kommer vi att observera en 10-procentig ökning av y för en enhetsförändring av x. För koefficienter med större absolutvärde rekommenderas att man beräknar exponenten.

När det gäller variabler inom ett intervall (t.ex. en procentsats) är det bekvämare för tolkningen att först multiplicera variabeln med 100 och sedan anpassa modellen. På så sätt blir tolkningen mer intuitiv, eftersom vi ökar variabeln med 1 procentenhet i stället för 100 procentenheter (från 0 till 1 omedelbart).

level-log-modell

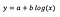
Låt oss anta att vi efter att ha anpassat modellen får:

Tolkningen av interceptet är densamma som för modellen på nivånivå.

För koefficienten b – en ökning av x med 1 % resulterar i en ungefärlig ökning av genomsnittligt y med b/100 (0,05 i detta fall), alla andra variabler hålls konstanta. För att få fram det exakta beloppet skulle vi behöva ta b× log(1,01), vilket i det här fallet ger 0,0498.

log-log-modell

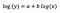
Låt oss anta att efter att ha anpassat modellen får vi:

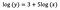
En gång till fokuserar jag på tolkningen av b. En ökning av x med 1 % resulterar i en 5 % ökning av det genomsnittliga (geometriska) y, alla andra variabler hålls konstanta. För att få fram det exakta beloppet måste vi ta

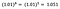
vilket är ~5,1%.

Slutsatser

Jag hoppas att den här artikeln har gett dig en översikt över hur man tolkar koefficienter för linjär regression, inklusive de fall då några av variablerna har logtransformerats. Som alltid är all konstruktiv feedback välkommen. Du kan nå mig på Twitter eller i kommentarerna.