Sammenligninger i relativitets- og kvantemekanikken (uden spin)
Indledning
-Tvivl om alting eller tro på alting er to lige bekvemme løsninger;
begge løsninger gør det ikke nødvendigt at reflektere.
Henri Poincaré (1854-1912)
Jeg ved det, jeg ved det, men tænk nu – tænk nu bare! – cirklens renhed har gjort os blinde for at se noget ud over den!
Jeg må begynde forfra med nye øjne, jeg må genoverveje alt!
Hypathia (∼360-415 e.Kr.)
I 1913 konstruerede Bohr på baggrund af Balmers empiriske formler en model af atomet baseret på kvantisering af banemængden , som senere blev suppleret med de mere generelle Sommerfeld-kvantiseringsregler. I disse år antog man naturligvis ikke tilstedeværelsen af et spin eller et iboende magnetisk moment hos partiklen eller især spin-orbit vekselvirkning eller vekselvirkning med kernespin.
I 1916 udledte Sommerfeld inden for rammerne af relativistiske tilgange en formel for energiniveauerne for et hydrogenlignende atom uden at tage hensyn til spin . Sommerfeld tog udgangspunkt i Bohr-atomets model og anvendte den relativistiske relation mellem impulsen og energien E for en fri partikel med massen m.
hvor c er lysets hastighed.
I et eksternt felt med et firedimensionalt potentiale (φ,A) blev det antaget, at for en partikel med ladningen qkan denne relation også anvendes, hvis vi trækker komponenterne af feltets firedimensionale impuls (qφ,qA) fra udtrykket for den generaliserede partikelimpuls:
I tilfælde af Coulombpotentialet φ=Ze/r, hvor e er elektronens ladning, ris afstanden fra kernen og Zer et atomnummer, får vi i sfæriske koordinater
hvor Lis vinkelimpulset. Bohr-Sommerfeld-kvantiseringsbetingelserne har formen
hvor nφog nrer henholdsvis det orbitale og det radiale kvantetal. For energiniveauerne opnåede Sommerfeld formlen
hvor det vigtigste kvantetal n=nr+l+1=1,2,3,…, l=0,1,2,3,…,n-1, og α=1/137,036er finstrukturkonstanten. I en artikel, der blev offentliggjort i 1916 , “begik Sommerfeld imidlertid en heldig fejl”, og den afledte formel blev præsenteret i følgende form
Formlen (6) beskrev perfekt alle de særlige kendetegn ved strukturen af spektret af brint og andre lignende atomer med den for disse år begrænsende nøjagtighed af målingerne, og der var ingen tvivl om selve formlens rigtighed. Derfor blev Sommerfeldformlen opfattet som empirisk, og i stedet for kvantetallet l blev der anvendt et “mystisk” internt kvantetal med halvt heltalsværdier j=1/2,3/2,5/2,…,n+1/2indført, og formel (6) blev anvendt i repræsentationen
hvor n=nr+j+1/2=1,2,3,…,j=1/2,3/2,5/2,…,n+1/2, og l besidder værdierne l=0 ved j=1/2og l=j±1/2for andre. Denne formel falder sammen med resultatet af en nøjagtig løsning af de relativistiske Dirac-ligninger i 1928 for en partikel med spin 1/2med det klassiske udtryk for den potentielle energi af en ubevægelig ladning i Coulomb-feltet for en kerne med atomnummer Zin i form af Ur=Ze2/r.
Formel (7) viste også en mærkelig begrænsning af værdien af ladningen af en kerne med atomnummer Z<137, over hvilken formlen mister sin betydning. Det var også tydeligt, at inden for rammerne af de skitserede tilgange, de stærke og gravitationelle vekselvirkninger, er planeternes bevægelser ikke beskrevet. Problemet Z<137eller α>1forbliver det uløste problem i den relativistiske kvantemekanik. Ved at udvide formlen (7) over rækkefølgen af potenser Zα2i Taylorrækken, med en ekspansionsnøjagtighed op til termerne ved potenserne Zα6, får vi
I 1925-1926 arbejdede Schrödinger på afledningen af ligningen for bølgefunktionen for en partikel, der beskriver De Broglie-bølgerne . Udledningen af ligningen var også baseret på den relativistiske relation (1) mellem impulsen og partiklens energi E, som han præsenterede ved hjælp af operatorer af energiens og impulsens kvadrater i form af en ligning for bølgefunktionen
Lignende Sommerfeld, Schrödinger brugte følgende repræsentation for en partikel i et ydre felt
I tilfælde af stationære tilstande af en ladet partikel i feltet af Coulombpotentialet for et brintatom var det nødvendigt at løse ligningen
Som det fremgår, at det kvadratiske udtryk for den potentielle energi q2φ2r/2mc2 er til stede i ligningen med et positivt fortegn, og i tilfælde af tiltrækkende felter fører løsningerne til visse vanskeligheder. Når man nærmer sig singularitetspunktet, stiger de tiltrækkende kræfter på grund af det negative fortegn, og tilstedeværelsen af singulariteten fører til kendte begrænsninger for størrelsen af vekselvirkningerne (figur 1).
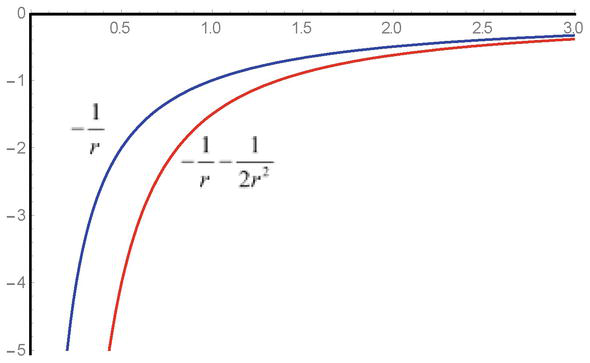
Figur 1.
Stikprøveafhængigheden af det tiltrækkende feltpotentiale-1/og den potentielle vekselvirkningsenergi-1/r-1/2r2i Klein-Gordon-ligningerne.
Dernæst er bølgevektoren kis repræsenteret som
og når man betragter problemet med passage af en partikel med energien Eth gennem en potentiel barriere U=qφr(Figur 2), hvis højde er større end partikelens dobbelte hvilenergi U>2mc2, bliver transmissionskoefficienten ens, uanset højden af barrieren (Klein-paradokset) .
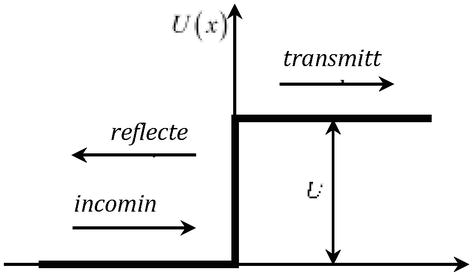
Figur 2.
Passage af en partikel gennem en potentiel barriereU.
En anden vanskelighed er, at som løsningen af partikelproblemet i en potentiel brønd viser, kan en partikel med en bølgelængde ƛ=ℏ/mcc ved tilstrækkelig dybde have bundne tilstande (kan lokaliseres) i en brøndbredde, der er smallere end partikelens bølgelængde d<ƛ/2(figur 3), hvilket er i modstrid med kvantemekanikkens grundlæggende princip – Heisenbergs usikkerhedsprincip.
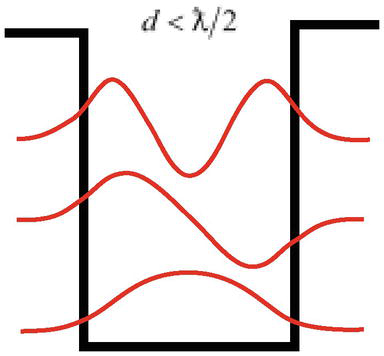
Figur 3.
En partikel med en bølgelængdeƛkan lokaliseres i en brøndbredded<ƛ/2.
Også løsningen af problemet med et brintlignende atom er begrænset af værdien af atomkernens ordinale nummer Z≤68(for Dirac-ligningen er begrænsningen af atomnummeret Z≤137). Det samme i relativistisk mekanik – når man overvejer stærke vekselvirkninger, angiver løsningen af den relativistiske Hamilton-Jacoby-ligning det såkaldte “partikelfald på centrum” .
For at slippe af med det kvadratiske udtryk eller vende dets fortegn er det i de senere år blevet foreslået at repræsentere potentiel energi i Klein-Gordon- og Dirac-ligningerne som forskellen af kvadrater fra udtrykkene for skalar- og vektorpotentialer (S-bølge ligning) . En sådan matematisk formalisme korrigerer situationen, men fra et fysisk synspunkt er sådanne repræsentationer på ingen måde berettigede, og de felter, der svarer til sådanne pseudopotentialer, eksisterer ikke i naturen.
Det er endnu værre med tilstedeværelsen af et kvadratisk udtryk i vektorfeltet, på grund af hvis fortegn vi får ikke-eksisterende tilstande i naturen og løsninger, der modsiger erfaringen.
I henhold til løsningerne af kvantemekanikkens og Hamilton-Jacobys ligninger, viser det sig, at en ladet partikel i et magnetfelt, ud over at rotere i en cirkel, også har radiale vibrationer-Landau-niveauer (selv i tilfælde af nul banemoment).
Igennem disse 90 år, især i meget nøjagtige cyklotronresonanseksperimenter, har ingen påvist elektronernes radialvibrationer og Landau-niveauerne.
Som løsning af denne ligning fik Schrödinger, ligesom Sommerfeld, formlen (5), som ikke præcist beskrev strukturen af brintspektret. Desuden viser det sig ud fra løsningen af problemet for en partikel i en potentiel brønd, at en partikel med en bølgelængde ƛ=ℏ/mchas bundne tilstande (er placeret) i en brønd af vilkårlig størrelse og især meget mindre end ƛ/2. Denne kendsgerning er i modstrid med kvante(bølge)teoriens grundlæggende princip, usikkerhedsprincippet.
I 1925 sendte Schrödinger dette arbejde til redaktørerne af ‘Annalen der Physik’ , men tog derefter manuskriptet, afviste de relativistiske tilgange og opbyggede i 1926 en bølgeligning baseret på det klassiske Hamiltonudtryk, Schrödinger-ligningen .
Geligningen beskrev kun kvalitativt brintatomets spektrum, men den havde dog ingen urimelige begrænsninger eller singulære løsninger i form af Sommerfeld-Dirac-formlen. Klein , Fock og Gordon offentliggjorde den relativistiske ligning baseret på bølgeligningen for en partikel uden spin i 1926; den kaldes Klein-Fock-Gordon-ligningen.
Med opdagelsen af spin ændrede situationen sig drastisk, og i 1926 viste Heisenberg og Jordan, at inden for Pauli-beskrivelsen af en elektrons spin, er halvdelen af energien i spin-orbit-interaktionen lig med et udtryk med en potens på α4 i Taylor-serieudvidelsen af Sommerfeld-formelens ligningsreference går her.
Hvorfor netop den halve, Thomas forsøgte at forklare dette i 1927 ved tilstedeværelsen af en relativistisk præcession af en elektron i referencerammen af bevægelse langs banen . Energien af Thomas’ præcession er præcis lig med halvdelen af værdien af energien af spin-orbit vekselvirkningen med det omvendte (positive) fortegn, som skal lægges til energien af spin-orbit vekselvirkningen. Den ukorrekte antagelse, at Thomas-præcessionsfrekvensen er identisk i begge referencerammer, og manglen på en fælles og korrekt udledning for ikke-inertielle (roterende) referencerammer har imidlertid givet anledning til tvivl om rigtigheden af sådanne fremgangsmåder. Årsagen til fremkomsten af halvdelen af spin-orbit-interaktionens energi i Sommerfeld-formlen er stadig under udredning og er et af de uløste problemer i moderne fysik.
På den anden side blev der både i afledningen af Sommerfeld-formlen og ved løsningen af Klein-Fock-Gordon-ligningen for brintatomproblemet , hverken spin- eller spin-orbit-interaktionsenergien oprindeligt taget i betragtning. Derfor kan den opnåede fine opsplitning på ingen måde skyldes spin-orbit-vekselvirkningen. Der er tale om en relativistisk, men rent mekanisk effekt, når en partikels masse (inerti) allerede afhænger af bevægelseshastigheden langs banen (vinkelmomentet), hvorved elektronens radiale bevægelse ændres og omvendt. Netop denne afhængighed, som resulterer i opsplitningen af elektronens energiniveauer og i umuligheden af at indføre kun ét, det vigtigste kvantetal. Ikke desto mindre, selv med denne antagelse, er rækkefølgen af niveauernes opsplitning i henhold til formel (8) i modstrid med logikken; det viser sig, at jo større orbital vinkelbevægelse, jo mindre energi i det opsplittede niveau.
Matrixrepræsentationen af andenordensbølgen Eq. (9) ved et system af ligninger af første orden er Dirac-konstruktionen af den relativistiske elektronligning (Dirac-matricerne er den særlige repræsentation af Clifford-Lipschitz-tallene ). I standardrepræsentationen har Dirac-ligningen for en fri partikel formen .
hvor
er Pauli-matricerne (enhedsmatricen i formlerne er udeladt).
For en partikel i et ydre felt gælder Eq. (16) normalt skrevet i formen
hvor for en invariant repræsentation i tilfælde af en fri partikel, er ligningerne sammensat for forskellen mellem det generaliserede momentum og feltets momentum.
I tilfældet med den potentielle energi af en ubevægelig ladning i et Coulomb-felt får vi Sommerfeld-Dirac-formlen som et resultat af en nøjagtig løsning af denne særlige ligning. Der er igen, selv om der for et system med spin 1/2 ikke i første omgang tages hensyn til energien af spin-orbit vekselvirkningen, men den halve fås fra den nøjagtige løsning af brintatomproblemet.
Mere nøjagtige målinger af Lamb i 1947 og efterfølgende forbedringer af brintatomets spektrum afslørede, at ud over linjerne med det maksimale j er alle de andre linjer også opdelt og noget forskudt (Lamb-skiftet). For at harmonisere teoriens resultater med mere præcise eksperimentelle data om brintatomets spektrum måtte man foreslå andre løsninger og tilgange end dem, der var fastlagt ved afledningen af Dirac-ligningen.
De nye teoretiske tilgange havde intet givet og supplerede kun teorien med de ulogiske og ikke-fysiske forslag til at overvinde den begyndende singularitet i løsningerne: renormalisering, den finitte forskel på uendeligheder med den ønskede værdi af forskellen osv. Ved at tage hensyn til kernenes størrelse blev kun Z-værdien korrigeret til en større værdi, men det løste ikke Z>137-problemet. Et utroligt resultat blev også opnået for brintatomproblemet, at elektronen højst sandsynligt befinder sig i atomets centrum, dvs. i kernen.
Resultaterne af løsningen af problemet for en partikel i en potentiel brønd både i tilfældet med Klein-Fock-Gordon-ligningen og med Dirac-ligningen er i modstrid med kvantemekanikkens grundprincip, usikkerhedsprincippet. Det fremgår af løsningerne, at en partikel kan befinde sig i en bundet tilstand i en brønd med vilkårlige dimensioner, især med en størrelse meget mindre end selve partikelens bølgelængde, A=ℏ/mc.
Men selv om Dirac selv foreslog et system af lineære første grads relativistiske ligninger i matrixrepræsentationen, der beskrev systemet med spin 1/2, forsvandt modsigelserne ikke, og han selv var utilfreds med resultaterne af sin teori. Som Dirac skrev i 1956 , kan udviklingen af den relativistiske elektronteori nu betragtes som et eksempel på, hvordan ukorrekte argumenter nogle gange fører til et værdifuldt resultat. I 70’erne blev det klart, at den relativistiske teori for kvantemekanikken ikke eksisterer, og at der bør søges efter nye, fundamentale tilgange og ligninger for at konstruere en konsistent teori for den relativistiske kvantemekanik. Og allerede i 80’erne talte Dirac om de uoverstigelige vanskeligheder ved den eksisterende kvanteteori og behovet for at skabe en ny .
Grunden til disse teoriers fiasko er ganske enkel – den ligger i, at man ignorerer vekselvirkningsenergiens afhængighed med feltet af partikelens hastighed. Systemets generaliserede impuls, partiklen plus det ydre felt, er summen af det relativistiske udtryk for partiklens mekaniske impuls og feltets impuls i tilfælde af vekselvirkning med den ubevægelige partikel
som ikke er en invariant repræsentation af partikelhastigheden. For at konstruere en eller anden invariant ud fra en sådan repræsentation blev der i alle tilfælde anvendt en “invariant” relation i form af en forskel mellem systemets generaliserede impuls og feltets impuls i tilfælde af vekselvirkning med den immobile partikel
Det er klart, at permutationen af komponenterne af den generaliserede impuls til opbygning af invarianten ikke løser det stillede problem. Udsagnet om, at udtrykket (20) er en partikels mekaniske impuls og derfor er en invariant, er ikke bevist, og det er nødvendigt at opfatte formlen (20) som en empirisk. Derfor er der ved høje hastigheder eller stærke vekselvirkninger en uberegnet afhængighed af energien i partikelens vekselvirkning med feltet af partikelens bevægelseshastighed, hvilket resulterer i fejlagtige resultater eller umulige beregninger.
I , blev der foreslået en invariant repræsentation af systemets generaliserede impuls, hvor der blev taget hensyn til afhængigheden af partikelens vekselvirkningsenergi med feltet af hastigheden:
som er den firedimensionelle repræsentation af systemets generaliserede impuls baseret på udtrykket for den generaliserede impuls for en ubevægelig partikel i en hviletilstand
hvis invariant altid er lig med udtrykket (19) uanset systemets tilstand.
Anvendelsen af variationsprincipper til at konstruere den relativistiske og kvanteteori var baseret på principperne for konstruktion af mekanikken ved hjælp af systemets lagrangian , som oprindeligt ikke var beregnet til relativistiske tilgange. Lagrangian-konstruktionen er parametrisk med den ene tidsvariabel τ = ct, der er udskilt fra variablerne i det firedimensionelle rum (resten er repræsenteret ved afhængigheden af denne variabel τ) og indeholder den samlede differentiel i forhold til denne variabel, partikelens hastighed. En sådan konstruktion er uacceptabel, fordi det er umuligt at anvende princippet om invarians af repræsentationen af variabler og den kovariante repræsentation af systemets handling.
I , at konstruere den relativistiske teori på grundlag af variationsprincipper, er de kanoniske (ikke-parametriske) løsninger af det variationelle problem for kanonisk definerede integralfunktionaler blevet overvejet, og de kanoniske løsninger af de variationelle problemer i mekanikken i Minkowski-rummene er skrevet. På grund af foreningen af de variationelle principper for mindste handling, flow og hyperflow fås de kanonisk invariante ligninger for det generaliserede momentum. Ud fra disse ligninger fås udtrykkene for aktionsfunktionen og bølgefunktionen som den generelle løsning af det forenede variationsproblem i mekanikken.
Nedenfor præsenterer vi det generaliserede invariansprincip og den tilsvarende repræsentation af systemets generaliserede impuls, ligningerne for relativistisk og kvantemekanik , giver løsningerne af problemerne med ladningsbevægelse i et konstant elektrisk felt, problemerne for en partikel i en potentiel brønd og passage af en partikel gennem en potentiel barriere, problemerne med bevægelse i et eksponentiel felt (Morse), problemerne med ladet partikel i et magnetisk felt, og også problemerne med et brintatom er givet.




