Gleichungen der Relativistischen und Quantenmechanik (ohne Spin)
Einführung
-Alles zu bezweifeln oder alles zu glauben sind zwei gleich bequeme Lösungen;
beide verzichten auf die Notwendigkeit des Nachdenkens.
Henri Poincaré (1854-1912)
Ich weiß, ich weiß, aber nehmen wir an – nur angenommen! –
Ich muss mit neuen Augen beginnen, ich muss alles überdenken!
Hypathia (∼360-415 n. Chr.)
Im Jahr 1913 konstruierte Bohr auf der Grundlage der empirischen Formeln von Balmer ein Atommodell, das auf der Quantisierung des Orbitalimpulses basierte und später durch die allgemeineren Sommerfeldschen Quantisierungsregeln ergänzt wurde. In jenen Jahren wurde natürlich das Vorhandensein eines Spins oder eines intrinsischen magnetischen Moments des Teilchens oder insbesondere eine Spin-Bahn-Wechselwirkung oder eine Wechselwirkung mit dem Kernspin nicht angenommen.
Im Jahr 1916 leitete Sommerfeld im Rahmen relativistischer Ansätze eine Formel für die Energieniveaus eines wasserstoffähnlichen Atoms ab, ohne den Spin zu berücksichtigen. Sommerfeld ging vom Modell des Bohr-Atoms aus und verwendete die relativistische Beziehung zwischen dem Impuls und der Energie E eines freien Teilchens mit der Masse m.
wobei cdie Lichtgeschwindigkeit ist.
In einem äußeren Feld mit einem vierdimensionalen Potential (φ,A) wurde angenommen, dass für ein Teilchen mit der Ladung qdiese Beziehung auch verwendet werden kann, wenn man vom Ausdruck für den verallgemeinerten Teilchenimpuls die Komponenten des vierdimensionalen Impulses des Feldes (qφ,qA) subtrahiert:
Im Fall des Coulomb-Potentials φ=Ze/r, wobei e die Ladung des Elektrons, ris der Abstand vom Kern und Z eine Ordnungszahl ist, erhalten wir in Kugelkoordinaten
wobei Lis der Drehimpuls ist. Die Bohr-Sommerfeld-Quantisierungsbedingungen haben die Form
wobei nφund ndie orbitalen bzw. radialen Quantenzahlen sind. Für die Energieniveaus erhielt Sommerfeld die Formel
wobei die Hauptquantenzahl n=nr+l+1=1,2,3,…, l=0,1,2,3,…,n-1, und α=1/137,036die Feinstrukturkonstante ist. In einem 1916 veröffentlichten Aufsatz unterlief Sommerfeld jedoch „ein glücklicher Fehler“, und die abgeleitete Formel wurde in der folgenden Form dargestellt
Die Formel (6) beschrieb perfekt alle Besonderheiten der Struktur des Spektrums von Wasserstoff und anderen ähnlichen Atomen mit der für diese Jahre begrenzten Genauigkeit der Messungen, und es gab keinen Zweifel an der Richtigkeit der Formel selbst. Daher wurde die Sommerfeld-Formel als empirisch angesehen, und anstelle der Quantenzahl l wurde eine „geheimnisvolle“ interne Quantenzahl mit halbzahligen Werten j=1/2,3/2,5/2,…,n+1/2 eingeführt, und Formel (6) wurde in der Darstellung
verwendet, wobei n=nr+j+1/2=1,2,3,…,j=1/2,3/2,5/2,…,n+1/2, und l die Werte l=0 bei j=1/2 und l=j±1/2 für andere besitzen. Diese Formel stimmt mit dem Ergebnis einer exakten Lösung der relativistischen Dirac-Gleichungen im Jahre 1928 für ein Teilchen mit dem Spin 1/2 mit dem klassischen Ausdruck für die potentielle Energie einer unbeweglichen Ladung im Coulomb-Feld eines Kerns mit der Ordnungszahl Zin in der Form Ur=Ze2/r überein.
Formel (7) zeigte auch eine merkwürdige Wertbegrenzung der Ladung eines Kerns mit der Ordnungszahl Z<137, über der die Formel ihre Bedeutung verliert. Es wurde auch deutlich, dass im Rahmen der skizzierten Ansätze, der starken und gravitativen Wechselwirkungen, die Bewegungen der Planeten nicht beschrieben werden. Das Problem Z<137 oder α>1 bleibt das ungelöste Problem der relativistischen Quantenmechanik. Erweitert man die Formel (7) über die Potenzordnung Zα2 in der Taylorreihe mit einer Expansionsgenauigkeit bis zu den Termen durch die Potenzen Zα6, so erhält man
In den Jahren 1925-1926 arbeitete Schrödinger an der Ableitung der Gleichung für die Wellenfunktion eines Teilchens, die die De Broglie-Wellen beschreibt. Die Herleitung der Gleichung basierte auch auf der relativistischen Beziehung (1) zwischen dem Impuls und der Energie E des Teilchens, die er mit Hilfe der Operatoren der Quadrate von Energie und Impuls in Form einer Gleichung für die Wellenfunktion
wie Sommerfeld darstellte, Schrödinger verwendete folgende Darstellung für ein Teilchen in einem äußeren Feld
Im Falle stationärer Zustände eines geladenen Teilchens im Feld des Coulomb-Potentials für ein Wasserstoffatom war es notwendig, die Gleichung
Wie man sieht, ist der quadratische Ausdruck der potentiellen Energie q2φ2r/2mc2 in der Gleichung mit positivem Vorzeichen vorhanden und im Falle von anziehenden Feldern führen die Lösungen zu gewissen Schwierigkeiten. Bei Annäherung an den Singularitätspunkt nehmen aufgrund des negativen Vorzeichens die Anziehungskräfte zu, und das Vorhandensein der Singularität führt zu den bekannten Beschränkungen für die Größe der Wechselwirkungen (Abbildung 1).
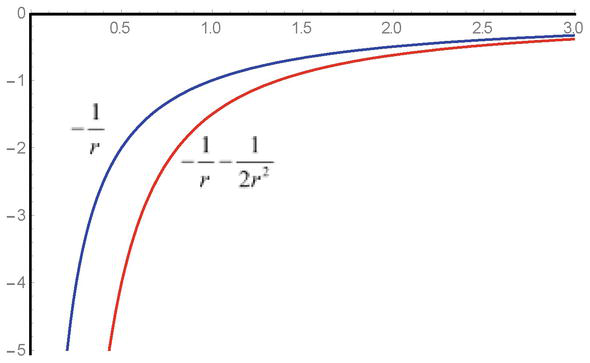
Abbildung 1.
Die Probenabhängigkeit des anziehenden Feldpotentials-1/rand potentielle Wechselwirkungsenergie-1/r-1/2r2in den Klein-Gordon-Gleichungen.
Der Wellenvektor kwird dargestellt als
und bei der Betrachtung des Problems des Durchgangs eines Teilchens mit der Energie Ethdurch eine Potentialbarriere U=qφr(Abbildung 2), deren Höhe größer ist als die doppelte Ruheenergie des Teilchens U>2mc2, wird der Transmissionskoeffizient unabhängig von der Höhe der Barriere eins (Klein-Paradoxon) .
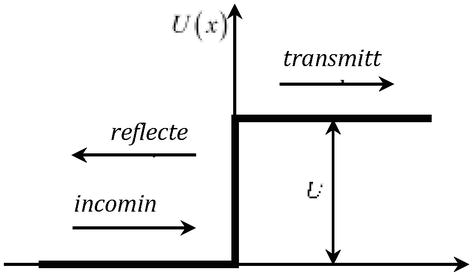
Abbildung 2.
Durchgang eines Teilchens durch eine PotentialbarriereU.
Eine weitere Schwierigkeit besteht darin, dass, wie die Lösung des Teilchenproblems in einem Potentialtopf zeigt, ein Teilchen mit einer Wellenlänge ƛ=ℏ/mcc in einer ausreichenden Tiefe gebundene Zustände haben kann (lokalisiert werden kann), die schmaler sind als die Wellenlänge des Teilchens d<ƛ/2(Abbildung 3), was dem Grundprinzip der Quantenmechanik – der Heisenbergschen Unschärferelation – widerspricht.
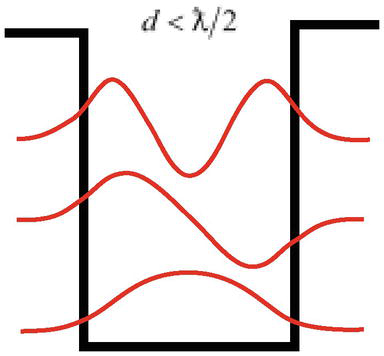
Abbildung 3.
Ein Teilchen mit einer Wellenlängeƛkann in einer Vertiefung der Breited<ƛ/2 lokalisiert werden.
Auch die Lösung des Problems eines wasserstoffähnlichen Atoms ist durch den Wert der Ordnungszahl des Atomkerns Z≤68 begrenzt (für die Dirac-Gleichung ist die Beschränkung der Ordnungszahl Z≤137). Dasselbe gilt für die relativistische Mechanik – wenn man starke Wechselwirkungen betrachtet, zeigt die Lösung der relativistischen Hamilton-Jacoby-Gleichung den so genannten „Teilchenfall auf das Zentrum“ an.
Um den quadratischen Term loszuwerden oder sein Vorzeichen umzukehren, wurde in den letzten Jahren vorgeschlagen, die potentielle Energie in den Klein-Gordon- und Dirac-Gleichungen als die Differenz der Quadrate aus den Ausdrücken der Skalar- und Vektorpotentiale darzustellen (S-Wellengleichung). Ein solcher mathematischer Formalismus korrigiert die Situation, aber vom physikalischen Standpunkt aus sind solche Darstellungen in keiner Weise gerechtfertigt, und die Felder, die solchen Pseudopotentialen entsprechen, existieren in der Natur nicht.
Noch schlimmer ist es mit dem Vorhandensein eines quadratischen Terms des Vektorfeldes, wegen dessen Vorzeichen wir in der Natur nicht existierende Zustände und Lösungen erhalten, die der Erfahrung widersprechen.
Nach den Lösungen der Gleichungen der Quantenmechanik und Hamilton-Jacoby, stellt sich heraus, dass ein geladenes Teilchen in einem Magnetfeld nicht nur kreisförmig rotiert, sondern auch radiale Schwingungen – Landau-Niveaus – hat (auch im Fall von Bahnimpuls Null).
In diesen 90 Jahren hat niemand, insbesondere in sehr genauen Zyklotronresonanz-Experimenten, die Radialschwingungen der Elektronen und die Landau-Niveaus nachgewiesen.
Bei der Lösung dieser Gleichung erhielt Schrödinger, wie Sommerfeld, die Formel (5), die die Struktur des Wasserstoffspektrums nicht genau beschrieb. Darüber hinaus ergibt sich aus der Lösung des Problems für ein Teilchen in einem Potentialtopf, dass ein Teilchen mit einer Wellenlänge ƛ=ℏ/mchas in einem Brunnen beliebiger Größe und insbesondere viel kleiner als ƛ/2 gebunden ist (ist). Diese Tatsache widerspricht dem Grundprinzip der Quanten(wellen)theorie, der Unschärferelation.
Im Jahr 1925 schickte Schrödinger diese Arbeit an die Redaktion der „Annalen der Physik“, nahm dann aber das Manuskript, lehnte die relativistischen Ansätze ab und stellte 1926 eine Wellengleichung auf, die auf dem klassischen Hamilton-Ausdruck, der Schrödinger-Gleichung, basiert.
Die Gleichung beschrieb das Spektrum des Wasserstoffatoms nur qualitativ, hatte aber keine unvernünftigen Einschränkungen oder singuläre Lösungen in Form der Sommerfeld-Dirac-Formel. Klein, Fock und Gordon veröffentlichten 1926 die auf der Wellengleichung basierende relativistische Gleichung für ein Teilchen ohne Spin; sie wird Klein-Fock-Gordon-Gleichung genannt.
Mit der Entdeckung des Spins änderte sich die Situation drastisch, und 1926 zeigten Heisenberg und Jordan, dass im Rahmen der Pauli-Beschreibung des Spins eines Elektrons die Hälfte der Energie der Spin-Bahn-Wechselwirkung gleich einem Term mit einer Potenz von α4 in der Taylor-Reihenentwicklung der Gleichung der Sommerfeld-Formel ist Referenz geht hier.
Warum genau die Hälfte, versuchte Thomas dies 1927 durch das Vorhandensein einer relativistischen Präzession eines Elektrons im Bezugsrahmen der Bewegung entlang der Bahn zu erklären. Die Energie der Thomas-Präzession entspricht genau der Hälfte der Energie der Spin-Bahn-Wechselwirkung mit umgekehrtem (positivem) Vorzeichen, die zur Energie der Spin-Bahn-Wechselwirkung addiert werden sollte. Die falsche Annahme, dass die Thomas-Präzessionsfrequenz in beiden Bezugssystemen identisch ist, und das Fehlen einer gemeinsamen und korrekten Ableitung für nichtinertiale (rotierende) Bezugssysteme haben jedoch Zweifel an der Richtigkeit solcher Ansätze aufkommen lassen. Der Grund für das Auftreten der halben Energie der Spin-Orbit-Wechselwirkung in der Sommerfeld-Formel wird immer noch untersucht und ist eines der ungelösten Probleme der modernen Physik.
Andererseits wurde sowohl bei der Herleitung der Sommerfeld-Formel als auch bei der Lösung der Klein-Fock-Gordon-Gleichung für das Wasserstoffatom-Problem zunächst weder der Spin noch die Energie der Spin-Orbit-Wechselwirkung berücksichtigt. Daher kann die erhaltene Feinaufspaltung in keiner Weise auf die Spin-Bahn-Wechselwirkung zurückzuführen sein. Dies ist ein relativistischer, aber rein mechanischer Effekt, bei dem die Masse (Trägheit) eines Teilchens bereits von der Bewegungsgeschwindigkeit entlang der Bahn (des Drehimpulses) abhängt, wodurch sich die radiale Bewegung des Elektrons ändert und umgekehrt. Genau diese Abhängigkeit, die zur Aufspaltung der Energieniveaus des Elektrons führt, und zur Unmöglichkeit, nur eine, die Hauptquantenzahl, einzuführen. Dennoch widerspricht auch bei dieser Annahme die Reihenfolge der Aufspaltung der Niveaus gemäß Formel (8) der Logik; es stellt sich heraus, dass die Energie des aufgespaltenen Niveaus umso geringer ist, je größer der Bahndrehimpuls ist.
Die Matrixdarstellung der Welle zweiter Ordnung Gl. (9) durch ein Gleichungssystem erster Ordnung ist die Dirac-Konstruktion der relativistischen Elektronengleichung (die Dirac-Matrizen sind die besondere Darstellung der Clifford-Lipschitz-Zahlen). In der Standarddarstellung hat die Dirac-Gleichung für ein freies Teilchen die Form .
wobei
die Pauli-Matrizen sind (die Einheitsmatrix wird in den Formeln weggelassen).
Für ein Teilchen in einem äußeren Feld wird Gl. (16) gewöhnlich in der Form
wobei für eine invariante Darstellung im Falle eines freien Teilchens die Gleichungen für die Differenz zwischen dem verallgemeinerten Impuls und dem Impuls des Feldes aufgestellt werden.
Im Fall der potentiellen Energie einer unbeweglichen Ladung in einem Coulomb-Feld erhält man die Sommerfeld-Dirac-Formel als Ergebnis einer exakten Lösung dieser speziellen Gleichung. Auch hier wird, obwohl für ein System mit Spin 1/2, die Energie der Spin-Bahn-Wechselwirkung zunächst nicht berücksichtigt, sondern die Hälfte aus der exakten Lösung des Wasserstoffatom-Problems gewonnen.
Genauere Messungen von Lamb im Jahr 1947 und spätere Verbesserungen des Spektrums des Wasserstoffatoms haben gezeigt, dass außer den Linien mit dem Maximum j auch alle anderen aufgespalten und etwas verschoben sind (die Lamb-Verschiebung). Um die Ergebnisse der Theorie mit den genaueren experimentellen Daten über das Spektrum des Wasserstoffatoms in Einklang zu bringen, musste man andere Lösungen und Ansätze vorschlagen, als sie durch die Herleitung der Dirac-Gleichung festgelegt waren.
Die neuen theoretischen Ansätze hatten nichts gebracht und ergänzten die Theorie nur mit unlogischen und unphysikalischen Vorschlägen, um die sich abzeichnende Singularität der Lösungen zu überwinden: die Renormierung, die endliche Differenz der Unendlichkeiten mit dem gewünschten Wert der Differenz, und so weiter. Die Berücksichtigung der Größe des Kerns korrigierte nur den Z-Wert zu einem größeren Wert, löste aber nicht das Z>137-Problem. Ein unglaubliches Ergebnis wurde auch für das Wasserstoffatom-Problem erzielt, dass sich das Elektron höchstwahrscheinlich im Zentrum des Atoms, also im Kern, befindet.
Die Ergebnisse der Lösung des Problems für ein Teilchen in einem Potentialtopf sowohl im Fall der Klein-Fock-Gordon-Gleichung als auch der Dirac-Gleichung widersprechen dem Grundprinzip der Quantenmechanik, der Unschärferelation. Aus den Lösungen geht hervor, dass sich ein Teilchen in einem Potentialtopf mit beliebigen Abmessungen in einem gebundenen Zustand befinden kann, insbesondere mit einer Größe, die viel kleiner ist als die Wellenlänge des Teilchens selbst, A=ℏ/mc.
Obwohl Dirac selbst ein System von linearen relativistischen Gleichungen ersten Grades in der Matrixdarstellung vorschlug, das das System mit Spin 1/2 beschrieb, verschwanden die Widersprüche nicht, und er selbst blieb mit den Ergebnissen seiner Theorie unzufrieden. Wie Dirac 1956 schrieb, kann die Entwicklung der relativistischen Elektronentheorie heute als ein Beispiel dafür angesehen werden, wie falsche Argumente manchmal zu einem wertvollen Ergebnis führen. In den 70er Jahren wurde klar, dass die relativistische Theorie der Quantenmechanik nicht existiert und dass neue, grundlegende Ansätze und Gleichungen gesucht werden sollten, um eine konsistente Theorie der relativistischen Quantenmechanik zu konstruieren. Und in den 80er Jahren sprach Dirac bereits von den unüberwindbaren Schwierigkeiten der bestehenden Quantentheorie und der Notwendigkeit, eine neue zu schaffen.
Der Grund für das Scheitern dieser Theorien ist ganz einfach – er liegt in der Ignorierung der Abhängigkeit der Wechselwirkungsenergie mit dem Feld von der Geschwindigkeit des Teilchens. Der verallgemeinerte Impuls des Systems, das Teilchen plus das äußere Feld, ist die Summe des relativistischen Ausdrucks für den mechanischen Impuls des Teilchens und den Feldimpuls im Falle der Wechselwirkung mit dem unbewegten Teilchen
was keine invariante Darstellung der Teilchengeschwindigkeit ist. Um aus einer solchen Darstellung eine Invariante zu konstruieren, wurde in allen Fällen eine „invariante“ Beziehung in Form einer Differenz zwischen dem verallgemeinerten Impuls des Systems und dem Feldimpuls im Fall der Wechselwirkung mit dem unbewegten Teilchen verwendet
Es ist offensichtlich, dass die Permutation der Komponenten des verallgemeinerten Impulses für die Konstruktion der Invariante das gestellte Problem nicht löst. Die Aussage, dass der Ausdruck (20) der mechanische Impuls eines Teilchens und damit eine Invariante ist, ist unbewiesen und es ist notwendig, die Formel (20) als empirisch zu begreifen. Daher kommt es bei hohen Geschwindigkeiten oder starken Wechselwirkungen zu einer unerklärten Abhängigkeit der Energie der Teilchenwechselwirkung mit dem Feld von der Geschwindigkeit der Teilchenbewegung, was zu fehlerhaften Ergebnissen oder der Unmöglichkeit von Berechnungen führt.
In wurde eine invariante Darstellung des verallgemeinerten Impulses des Systems vorgeschlagen, bei der die Abhängigkeit der Wechselwirkungsenergie des Teilchens mit dem Feld von der Geschwindigkeit berücksichtigt wurde:
die die vierdimensionale Darstellung des verallgemeinerten Impulses des Systems ist, die auf dem Ausdruck für den verallgemeinerten Impuls eines unbewegten Teilchens im Ruhezustand
beruht, dessen Invariante unabhängig vom Zustand des Systems immer gleich dem Ausdruck (19) ist.
Die Anwendung der Variationsprinzipien zur Konstruktion der relativistischen und der Quantentheorie basierte auf den Prinzipien der Konstruktion der Mechanik mit Hilfe der Lagrange des Systems, die ursprünglich nicht für relativistische Ansätze gedacht war. Die Lagrange-Konstruktion ist parametrisch mit der einen Zeitvariablen τ = ct, die aus den Variablen des vierdimensionalen Raums herausgehoben ist (die übrigen werden durch die Abhängigkeit von dieser Variablen τ dargestellt) und das Gesamtdifferential in Bezug auf diese Variable, die Geschwindigkeit des Teilchens, enthält. Eine solche Konstruktion ist inakzeptabel, weil es unmöglich ist, das Prinzip der Invarianz der Darstellung der Variablen und der kovarianten Darstellung der Wirkung des Systems anzuwenden.
Um die relativistische Theorie auf der Grundlage von Variationsprinzipien zu konstruieren, wurden die kanonischen (nicht parametrischen) Lösungen des Variationsproblems für kanonisch definierte integrale Funktionale betrachtet und die kanonischen Lösungen der Variationsprobleme der Mechanik in den Minkowski-Räumen geschrieben. Durch die Vereinheitlichung der Variationsprinzipien der kleinsten Wirkung, des Flusses und des Hyperflusses erhält man die kanonisch invarianten Gleichungen für den verallgemeinerten Impuls. Aus diesen Gleichungen werden die Ausdrücke für die Aktionsfunktion und die Wellenfunktion als allgemeine Lösung des vereinheitlichten Variationsproblems der Mechanik gewonnen.
Im Folgenden werden das verallgemeinerte Invarianzprinzip und die entsprechende Darstellung des verallgemeinerten Impulses des Systems, die Gleichungen der relativistischen und der Quantenmechanik vorgestellt, die Lösungen der Probleme der Ladungsbewegung in einem konstanten elektrischen Feld, die Probleme für ein Teilchen in einem Potentialtopf und der Durchgang eines Teilchens durch eine Potentialbarriere, die Probleme der Bewegung in einem exponentiellen Feld (Morse), die Probleme des geladenen Teilchens in einem magnetischen Feld und auch die Probleme eines Wasserstoffatoms angegeben.




