A relativisztikus és kvantummechanika egyenletei (spin nélkül)
Bevezetés
-Kételkedni mindenben vagy hinni mindenben két egyformán kényelmes megoldás;
mindkettő nélkülözi a reflexió szükségességét.
Henri Poincaré (1854-1912)
– Tudom, tudom, de tegyük fel – csak tegyük fel! – a kör tisztasága elvakított minket attól, hogy bármit is lássunk rajta túl!
Új szemmel kell kezdenem az egészet, mindent újra kell gondolnom!
Hypathia (∼360-415 Kr.u.)
1913-ban Bohr a Balmer-féle empirikus képletekre alapozva megalkotta az atom modelljét, amely a keringési nyomaték kvantálásán alapult , és amelyet később kiegészítettek az általánosabb Sommerfeld-féle kvantálási szabályokkal. Ezekben az években természetesen nem feltételezték a spin vagy a részecske saját mágneses nyomatékának jelenlétét, vagy különösen a spin-pálya kölcsönhatást, illetve a nukleáris spinnel való kölcsönhatást.
1916-ban Sommerfeld a relativisztikus megközelítések keretében levezetett egy képletet a hidrogénszerű atom energiaszintjeire, a spin figyelembevétele nélkül . Sommerfeld a Bohr-atom modelljéből indult ki, és az m tömegű szabad részecske E energiája és impulzusa közötti relativisztikus összefüggést használta.
ahol ca fénysebesség.
Négydimenziós potenciállal (φ,A) rendelkező külső térben feltételezték, hogy egy q töltésű részecske esetén ez az összefüggés akkor is használható, ha a tér négydimenziós impulzusának (qφ,qA) komponenseit kivonjuk az általánosított részecskeimpulzus kifejezéséből:
A φ=Ze/r Coulomb-potenciál esetén, ahol e az elektron töltése, ris az atommagtól való távolság, Zaz atomszám, gömbkoordinátákban
ahol Lis a szögimpulzus. A Bohr-Sommerfeld kvantálási feltételek a következő alakot veszik fel
mivel nφés nraz orbitális, illetve radiális kvantumszámok. Az energiaszintekre Sommerfeld a következő képletet kapta
ahol a fő kvantumszám n=nr+l+1=1,2,3,…, l=0,1,2,3,…,n-1, és α=1/137,036a finomszerkezeti állandó. Egy 1916-ban megjelent tanulmányában azonban Sommerfeld “szerencsés hibát követett el”, és a levezetett képletet a következő formában adta meg
A (6) képlet tökéletesen leírta a hidrogén és más hasonló atomok spektrumszerkezetének minden sajátosságát az akkori mérési pontosságot korlátozó mérési pontossággal, és magának a képletnek a helyességéhez sem férhetett kétség. Ezért a Sommerfeld-formulát empirikusnak fogták fel, és az l kvantumszám helyett egy “titokzatos” belső kvantumszámot, a j=1/2,3/2,5/2,… fél egész értékekkel.,n+1/2 -et vezettek be, és a (6) képletet a
ábrázolásban használták, ahol n=nr+j+1/2=1,2,3,…,j=1/2,3/2,5/2,…,n+1/2, és l a j=1/2-nél l=0, a többinél l=j±1/2 értékekkel rendelkezik. Ez a képlet egybeesik a relativisztikus Dirac-egyenletek 1928-ban egy 1/2 spinű részecskére adott pontos megoldásának eredményével és a Zin atomszámú atommag Coulomb-mezőben mozdulatlan töltés potenciális energiájának klasszikus kifejezésével Ur=Ze2/r.
A (7) képlet egy furcsa értékhatárt is jelzett a Z<137 atomszámú atommag töltésének, amely felett a képlet értelmét veszti. Az is nyilvánvalóvá vált, hogy a vázolt megközelítések, az erős és a gravitációs kölcsönhatás keretein belül a bolygók mozgása nem írható le. A Z<137vagy α>1probléma a relativisztikus kvantummechanika megoldatlan problémája marad. A (7) képletet a Zα2 nagyságrendű hatványokra a Taylor-sorozatban felbontva, a Zα6 hatványok szerinti tagokig terjedő pontossággal, megkapjuk
1925-1926-ban Schrödinger a De Broglie-hullámokat leíró részecske hullámfüggvény egyenletének levezetésén dolgozott . Az egyenlet levezetése is a részecske E energiája és a lendület pand közötti relativisztikus összefüggésen (1) alapult, amelyet az energia és az impulzus négyzetoperátorainak segítségével a hullámfüggvény
egyenlet formájában mutatott be Sommerfeldhez hasonlóan, Schrödinger a következő ábrázolást használta egy külső mezőben lévő részecskére
Sztacionárius állapotok esetén egy töltött részecske a hidrogénatom Coulomb-potenciáljának mezejében a következő egyenletet kellett megoldani
Mint látható, a q2φ2r/2mc2potenciális energia kvadratikus kifejezése pozitív előjellel szerepel az egyenletben, és vonzó mezők esetén a megoldások bizonyos nehézségekhez vezetnek. A szingularitási ponthoz közeledve a negatív előjel miatt a vonzóerők megnőnek, és a szingularitás jelenléte a kölcsönhatások nagyságának ismert korlátaihoz vezet (1. ábra).
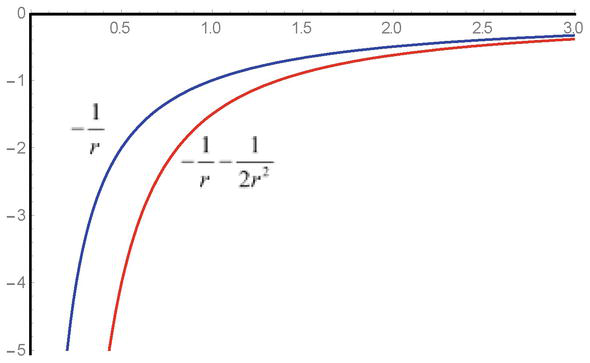
1. ábra.
A vonzó mező potenciál-1/és potenciális kölcsönhatási energia-1/r-1/2r2mintafüggése a Klein-Gordon-egyenletekben.
A továbbiakban a kis hullámvektort a következőképpen ábrázoljuk
és ha egy Eth energiájú részecske áthaladásának problémáját vizsgáljuk egy potenciális akadályon U=qφr(2. ábra), amelynek magassága nagyobb, mint a részecske megduplázott nyugalmi energiája U>2mc2 , az áteresztési együttható az akadály magasságától függetlenül egységessé válik (Klein-paradoxon) .
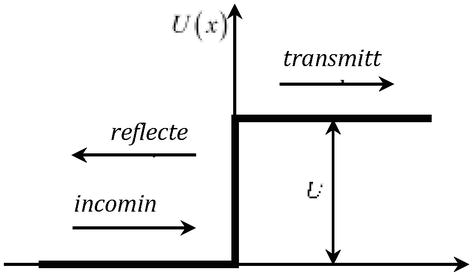
2. ábra.
Egy részecske áthaladása egy potenciális akadályonU.
Egy másik nehézség az, hogy – mint a részecskeprobléma potenciálgödörben való megoldása mutatja – kellő mélységben egy ƛ=ℏ/mcc hullámhosszúságú részecskének lehetnek kötött állapotai (lokalizálhatók) a részecske d<ƛ/2 hullámhosszánál keskenyebb kútszélességben (3. ábra), ami ellentmond a kvantummechanika alapelvének – a Heisenberg-féle bizonytalansági elvnek.
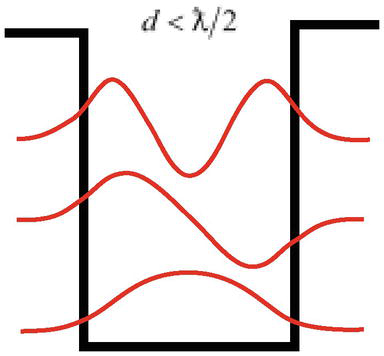
3. ábra.
Azƛ hullámhosszúságú részecske d<ƛ/2 szélességű kútban lokalizálható.
A hidrogénszerű atom problémájának megoldását korlátozza továbbá az atommag rendszámának Z≤68 értéke(a Dirac-egyenlet esetében az atomszám korlátozása Z≤137). Ugyanez a helyzet a relativisztikus mechanikában – az erős kölcsönhatások figyelembevételekor a Hamilton-Jacoby relativisztikus egyenlet megoldása az úgynevezett “részecske középpontra esését” jelzi .
A négyzetes tagtól való megszabadulás vagy annak előjelének megfordítása érdekében az utóbbi években azt javasolták, hogy a Klein-Gordon- és Dirac-egyenletekben a potenciális energiát a skalár- és vektorpotenciálok kifejezéseinek négyzetkülönbségeként ábrázolják (S-hullámegyenlet) . Egy ilyen matematikai formalizmus korrigálja a helyzetet, de fizikai szempontból az ilyen ábrázolások semmiképpen sem indokoltak, és az ilyen álpotenciáloknak megfelelő mezők nem léteznek a természetben.
A dolgok még rosszabbul állnak a vektormező kvadratikus tagjának jelenlétével, amelynek előjele miatt a természetben nem létező állapotokat és a tapasztalatoknak ellentmondó megoldásokat kapunk.
A kvantummechanika és Hamilton-Jacoby egyenleteinek megoldásai szerint, kiderül, hogy a mágneses térben lévő töltött részecske a körkörös forgáson kívül sugárirányú rezgésekkel – Landau-szintekkel – is rendelkezik (még nulla keringési impulzus esetén is).
A 90 év alatt, különösen a nagyon pontos ciklotronrezonancia-kísérletekben, senki sem tudta kimutatni az elektronok radiális rezgéseit és a Landau-szinteket.
Ezt az egyenletet megoldva Schrödinger, Sommerfeldhez hasonlóan, megkapta az (5) képletet, amely nem pontosan írta le a hidrogén spektrumának szerkezetét. Sőt, a feladat megoldásából egy potenciálkútban lévő részecskére vonatkozóan kiderül, hogy egy ƛ=ℏ/mchas hullámhosszúságú részecske kötött állapotokat (helyez el) egy tetszőleges méretű és különösen ƛ/2-nél jóval kisebb kútban. Ez a tény ellentmond a kvantum(hullám)elmélet alapelvének, a bizonytalansági elvnek.
1925-ben Schrödinger elküldte ezt a munkát az “Annalen der Physik” szerkesztőségének , de aztán a kéziratot átvette, elutasította a relativista megközelítéseket, és 1926-ban a klasszikus Hamilton-egyenleten alapuló hullámegyenletet, a Schrödinger-egyenletet építette fel.
Az egyenlet csak kvalitatív módon írta le a hidrogénatom spektrumát, azonban a Sommerfeld-Dirac-képlet formájában nem rendelkezett ésszerűtlen korlátozásokkal vagy szinguláris megoldásokkal. Klein , Fock és Gordon 1926-ban publikálta a hullámegyenleten alapuló relativisztikus egyenletet spin nélküli részecskére; ezt Klein-Fock-Gordon egyenletnek nevezik.
A spin felfedezésével a helyzet drasztikusan megváltozott, és 1926-ban Heisenberg és Jordan megmutatta, hogy az elektron spinjének Pauli-féle leírásán belül a spin-orbit kölcsönhatás energiájának fele egyenlő a Sommerfeld-egyenlet Taylor-soros kiterjesztésének α4-es hatványú tagjával, a Sommerfeld-egyenletre való hivatkozás ide megy.
Miért pont a fele, ezt Thomas 1927-ben az elektron relativisztikus precessziójának jelenlétével próbálta megmagyarázni a pálya mentén a vonatkoztatási rendszerben . A Thomas-féle precesszió energiája pontosan a spin-orbit kölcsönhatás inverz (pozitív) előjelű energiájának felével egyenlő, amit hozzá kell adni a spin-orbit kölcsönhatás energiájához. Az a helytelen feltételezés azonban, hogy a Thomas-precesszió frekvenciája mindkét vonatkoztatási rendszerben azonos, valamint a nem inerciális (forgó) vonatkoztatási rendszerekre vonatkozó közös és helyes levezetés hiánya kétségeket ébresztett az ilyen megközelítések helyességével kapcsolatban. A spin-orbit kölcsönhatás energiájának felének a Sommerfeld-képletben való megjelenésének az okát még mindig vizsgálják, és ez a modern fizika egyik megoldatlan problémája.
Másrészt, mind a Sommerfeld-képlet levezetésénél, mind a Klein-Fock-Gordon-egyenlet megoldásánál a hidrogénatom-problémára , sem a spin, sem a spin-orbit kölcsönhatás energiáját nem vették kezdetben figyelembe. Ezért a kapott finom hasadás semmiképpen sem lehet a spin-orbit kölcsönhatásnak köszönhető. Ez egy relativisztikus, de tisztán mechanikai hatás, amikor a részecske tömege (tehetetlensége) már a pálya mentén történő mozgás sebességétől (a szögnyomatéktól) függ, ami miatt az elektron sugárirányú mozgása megváltozik, és fordítva. Éppen ez a függés, ami az elektron energiaszintjeinek felhasadását eredményezi, és azt, hogy nem lehet csak egyet, a fő kvantumszámot bevezetni. Mindazonáltal még ezzel a feltételezéssel is ellentmond a (8. képlet szerinti szintek felhasadási sorrendje a logikának; kiderül, hogy minél nagyobb a keringési nyomaték, annál kisebb a felhasított szint energiája.
A másodrendű hullám mátrixos ábrázolása Eq. (9) első rendű egyenletrendszerrel való ábrázolása a relativisztikus elektronegyenlet Dirac-konstrukciója (a Dirac-mátrixok a Clifford-Lipschitz-számok sajátos ábrázolása ). A szabványos ábrázolásban a szabad részecskére vonatkozó Dirac-egyenlet a következő formájú .
ahol
a Pauli-mátrixok (az egységmátrixot a képletekben elhagyjuk).
Egy külső térben lévő részecske esetében az egyenlet. (16) egyenletet általában
ahol egy szabad részecske esetén invariáns ábrázolás esetén az egyenletek az általánosított impulzus és a mező impulzusának különbségére állnak össze.
Coulomb-térben mozdulatlan töltés potenciális energiája esetén e sajátos egyenlet egzakt megoldásának eredményeként kapjuk a Sommerfeld-Dirac-formulát. Ott is, bár egy 1/2 spinű rendszer esetében a spin-orbit kölcsönhatás energiáját kezdetben nem vesszük figyelembe, de a felét a hidrogénatom problémájának pontos megoldásából kapjuk.
A hidrogénatom spektrumának 1947-ben végzett pontosabb Lamb-mérései és az azt követő fejlesztések kimutatták, hogy a j maximumú vonalak mellett az összes többi vonal is kettéválik és némileg elmozdul (Lamb-eltolódás). Az elmélet eredményeinek a hidrogénatom spektrumára vonatkozó pontosabb kísérleti adatokkal való összehangolásához más megoldásokat és megközelítéseket kellett javasolni, mint amiket a Dirac-egyenlet levezetése lefektetett.
Az új elméleti megközelítések semmit sem hoztak, és csak kiegészítették az elméletet a megoldások kialakuló szingularitásának leküzdésére tett logikátlan és nem fizikai javaslatokkal: a renormálással, a végtelenek véges különbségével a különbség kívánt értékével és így tovább. Az atommag méretének figyelembevétele csak a Z-értéket korrigálta nagyobb értékre, de nem oldotta meg a Z>137problémát. A hidrogénatom problémájára is hihetetlen eredményt kaptunk, hogy az elektron nagy valószínűséggel az atom középpontjában, azaz az atommagban helyezkedik el.
A potenciálgödörben lévő részecskére vonatkozó probléma megoldásának eredményei mind a Klein-Fock-Gordon-egyenlet, mind a Dirac-egyenlet esetében ellentmondanak a kvantummechanika alapelvének, a bizonytalansági elvnek. A megoldásokból kiderül, hogy egy részecske tetszőleges méretű, különösen a részecske hullámhosszánál jóval kisebb méretű, A=ℏ/mc hullámhosszúságú kútban is lehet kötött állapotban.
Nem hiába javasolt maga Dirac egy olyan lineáris elsőfokú relativisztikus egyenletrendszert a mátrixábrázolásban, amely leírja az 1/2-es spinű rendszert, az ellentmondások nem szűntek meg, és ő maga is elégedetlen maradt elméletének eredményeivel. Ahogy Dirac 1956-ban írta , a relativisztikus elektronelmélet fejlődése ma már példának tekinthető arra, hogy a helytelen érvek néha értékes eredményre vezetnek. A 70-es években világossá vált, hogy a relativisztikus kvantummechanika elmélete nem létezik, és új, alapvető megközelítéseket és egyenleteket kell keresni a relativisztikus kvantummechanika konzisztens elméletének felépítéséhez. A 80-as években pedig Dirac már a létező kvantumelmélet leküzdhetetlen nehézségeiről és egy új elmélet megalkotásának szükségességéről beszélt .
Az elméletek kudarcának oka igen egyszerű – a mezővel való kölcsönhatási energiának a részecske sebességétől való függésének figyelmen kívül hagyásában rejlik. A rendszer, a részecske plusz a külső mező általánosított impulzusa a részecske mechanikai impulzusának és a mező impulzusának relativisztikus kifejezésének összege a mozdulatlan részecskével való kölcsönhatás esetén
amely nem a részecske sebességének invariáns ábrázolása. Ahhoz, hogy egy ilyen reprezentációból valamilyen invariánst konstruáljunk, minden esetben egy “invariáns” összefüggést használtunk a rendszer általánosított impulzusa és a mezőimpulzus közötti különbség formájában a mozdulatlan részecskével való kölcsönhatás esetén
Az általános impulzus komponensek permutációja az invariáns felépítéséhez nyilvánvalóan nem oldja meg a felvetett problémát. Az az állítás, hogy a (20) kifejezés a részecske mechanikai impulzusa és ezért invariáns, nem bizonyított, és a (20) képletet empirikusnak kell felfogni. Ezért nagy sebességeknél vagy erős kölcsönhatásoknál a részecske és a mező kölcsönhatásának energiája számolatlanul függ a részecske mozgásának sebességétől, ami hibás eredményekhez vagy a számítások lehetetlenségéhez vezet.
Az , a rendszer általánosított impulzusának invariáns ábrázolását javasolták, ahol figyelembe vették a részecske és a mező kölcsönhatási energiájának a sebességtől való függését:
amely a rendszer általánosított impulzusának négydimenziós ábrázolása a nyugalmi állapotban lévő mozdulatlan részecske általánosított impulzusának kifejezése alapján
amely invariáns a rendszer állapotától függetlenül mindig egyenlő a (19) kifejezéssel.
A variációs elvek alkalmazása a relativisztikus és kvantumelmélet felépítésére a mechanika felépítésének elvein alapult a rendszer Lagrange-je segítségével , amit eredetileg nem relativisztikus megközelítésekre szántak. A Lagrange-konstrukció a négydimenziós tér változói közül kiemelt τ = ct egyetlen időváltozóval parametrikus (a többit ettől a τ változótól való függés reprezentálja), és tartalmazza az e változóhoz viszonyított teljes differenciált, a részecske sebességét. Egy ilyen konstrukció elfogadhatatlan, mert nem lehet alkalmazni a változók reprezentációjának invariáns elvét és a rendszer hatásának kovariáns reprezentációját.
A relativisztikus elmélet variációs elvek alapján történő felépítéséhez a variációs probléma kanonikus (nem parametrikus) megoldásait kanonikusan meghatározott integrálfüggvényekre vették figyelembe, és felírták a mechanika variációs problémáinak kanonikus megoldásait a Minkowski terekben. A legkisebb hatás, az áramlás és a hiperáramlás variációs elveinek egyesítése miatt megkapjuk az általánosított impulzusok kanonikusan invariáns egyenleteit. Ezekből az egyenletekből a mechanika egységesített variációs problémájának általános megoldásaként megkapjuk a hatásfüggvény és a hullámfüggvény kifejezéseit.
A következőkben bemutatjuk az általánosított invarienciaelvet és a rendszer általánosított impulzusának megfelelő ábrázolását, a relativisztikus és kvantummechanika egyenleteit , megadjuk az állandó elektromos térben való töltésmozgás problémáinak megoldásait, a potenciálkutakban lévő részecske problémáit és a részecske potenciálgáton való áthaladásának problémáit, az exponenciális térben (Morse) való mozgás problémáit, a mágneses térben lévő töltött részecske problémáit, valamint a hidrogénatom problémáit is megadjuk.




