Cuestiones de la Mecánica Relativista y Cuántica (sin Spin)
Introducción
Dudar de todo o creerlo todo son dos soluciones igualmente convenientes;
ambas prescinden de la necesidad de reflexión.
Henri Poincaré (1854-1912)
Lo sé, lo sé, pero supongamos -¡sólo supongamos! – la pureza del círculo nos ha impedido ver nada más allá de él!
¡Debo empezar de nuevo con ojos nuevos, debo replanteármelo todo!
Hipatía (∼360-415 d.C.)
En 1913, Bohr, basándose en las fórmulas empíricas de Balmer, construyó un modelo de átomo basado en la cuantización del momento orbital , que posteriormente se complementó con las reglas de cuantización más generales de Sommerfeld. En aquellos años, naturalmente, no se suponía la presencia de un espín o de un momento magnético intrínseco de la partícula ni, sobre todo, la interacción espín-órbita, o la interacción con el espín nuclear.
En 1916, Sommerfeld, en el marco de los planteamientos relativistas, derivó una fórmula para los niveles de energía de un átomo tipo hidrógeno, sin tener en cuenta el espín . Sommerfeld partió del modelo del átomo de Bohr y utilizó la relación relativista entre el momento pand la energía Ede una partícula libre con la masa m.
donde c es la velocidad de la luz.
En un campo externo con un potencial cuatridimensional (φ,A), se supuso que para una partícula con la carga qesta relación también se puede utilizar si restamos las componentes del momento cuatridimensional del campo (qφ,qA) de la expresión para el momento generalizado de la partícula:
En el caso del potencial de Coulomb φ=Ze/r, donde e es la carga del electrón, ris la distancia al núcleo, y Zes un número atómico, obtenemos en coordenadas esféricas
donde Lis el momento angular. Las condiciones de cuantificación de Bohr-Sommerfeld toman la forma
donde nφy nrson los números cuánticos orbital y radial, respectivamente. Para los niveles de energía, Sommerfeld obtuvo la fórmula
donde el número cuántico principal n=nr+l+1=1,2,3,…, l=0,1,2,3,…,n-1, y α=1/137,036es la constante de estructura fina. Sin embargo, en un artículo publicado en 1916 , Sommerfeld «cometió un afortunado error» y la fórmula derivada se presentó de la siguiente forma
La fórmula (6) describía perfectamente todas las peculiaridades de la estructura del espectro del hidrógeno y de otros átomos similares con la precisión limitante para aquellos años de las mediciones, y no había ninguna duda sobre la corrección de la propia fórmula. Por lo tanto, la fórmula de Sommerfeld fue percibida como empírica, y en lugar del número cuántico l, se introdujo un «misterioso» número cuántico interno con valores medio enteros j=1/2,3/2,5/2,…,n+1/2, y se utilizó la fórmula (6) en la representación
donde n=nr+j+1/2=1,2,3,…,j=1/2,3/2,5/2,…,n+1/2, y l posee los valores l=0en j=1/2 y l=j±1/2 para los demás. Esta fórmula coincide con el resultado de una solución exacta de las ecuaciones relativistas de Dirac en 1928 para una partícula con el espín 1/2con la expresión clásica para la energía potencial de una carga inmóvil en el campo de Coulomb de un núcleo con un número atómico Zen la forma Ur=Ze2/r.
La fórmula (7) también indicó una extraña limitación del valor la carga de un núcleo con el número atómico Z<137, por encima de la cual la fórmula pierde su significado. También era evidente que en el marco de los planteamientos expuestos, las interacciones fuertes y gravitatorias, no se describen los movimientos de los planetas. El problema Z<137 o α>1 sigue siendo el problema no resuelto de la mecánica cuántica relativista. Expandiendo la fórmula (7) sobre el orden de potencias Zα2en la serie de Taylor, con una precisión de expansión hasta los términos por las potencias Zα6, se obtiene
En 1925-1926, Schrödinger trabajó en la derivación de la ecuación para la función de onda de una partícula que describe las ondas de De Broglie . La derivación de la ecuación también se basó en la relación relativista (1) entre el momento pand la energía Ede la partícula, que presentó con la ayuda de los operadores de cuadrados de la energía y el momento en forma de una ecuación para la función de onda
Al igual que Sommerfeld, Schrödinger utilizó la siguiente representación para una partícula en un campo externo
En el caso de estados estacionarios de una partícula cargada en el campo del potencial de Coulomb para un átomo de hidrógeno fue necesario resolver la ecuación
Como puede verse, la expresión cuadrática de la energía potencial q2φ2r/2mc2está presente en la ecuación con signo positivo y en el caso de campos atractores, las soluciones conducen a ciertas dificultades. Al acercarse al punto de singularidad, debido al signo negativo, las fuerzas atractivas aumentan y la presencia de la singularidad conduce a limitaciones conocidas en la magnitud de las interacciones (Figura 1).
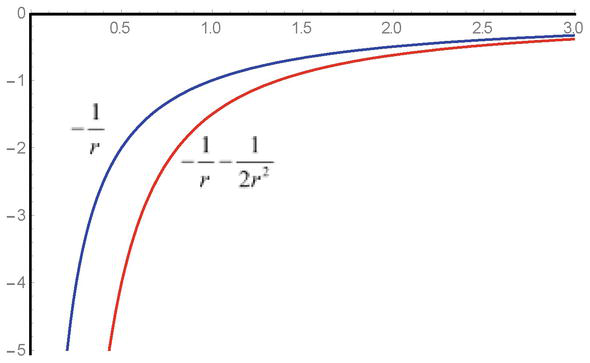
Figura 1.
La dependencia de la muestra del potencial de campo atractivo-1/y de la energía de interacción potencial-1/r-1/2r2en las ecuaciones de Klein-Gordon.
A continuación, el vector de onda kse representa como
y al considerar el problema del paso de una partícula con energía Eth por una barrera de potencial U=qφr(Figura 2), cuya altura es mayor que la energía doble de reposo de la partícula U>2mc2, el coeficiente de transmisión se convierte en la unidad, independientemente de la altura de la barrera (paradoja de Klein) .
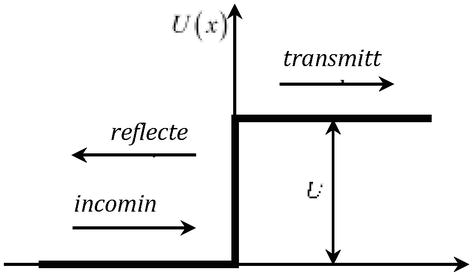
Figura 2.
Paso de una partícula a través de una barrera potencialU.
Otra dificultad es que, como muestra la solución del problema de la partícula en un pozo de potencial, a una profundidad suficiente, una partícula con una longitud de onda ƛ=ℏ/mc puede tener estados ligados (puede localizarse) en un ancho de pozo más estrecho que la longitud de onda de la partícula d<ƛ/2(Figura 3), lo que contradice el principio fundamental de la mecánica cuántica: el principio de incertidumbre de Heisenberg.
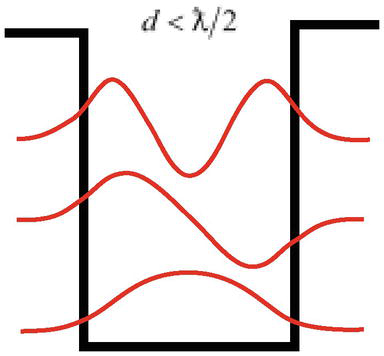
Figura 3.
Una partícula con una longitud de ondaƛ puede ser localizada en un pozo de anchurad<ƛ/2.
Además, la solución del problema de un átomo tipo hidrógeno está limitada por el valor del número ordinal del núcleo atómico Z≤68(para la ecuación de Dirac, la restricción del número atómico es Z≤137). Lo mismo en la mecánica relativista-cuando se consideran las interacciones fuertes, la solución de la ecuación relativista de Hamilton-Jacoby indica la llamada «caída de la partícula en el centro» .
Para deshacerse del término cuadrático o invertir su signo, en los últimos años se ha propuesto representar la energía potencial en las ecuaciones de Klein-Gordon y Dirac como la diferencia de cuadrados de las expresiones de los potenciales escalares y vectoriales (ecuación de la onda S) . Tal formalismo matemático corrige la situación, pero desde el punto de vista físico tales representaciones no están en absoluto justificadas, y los campos correspondientes a tales pseudopotenciales no existen en la naturaleza.
Las cosas son aún peores con la presencia de un término cuadrático del campo vectorial, por cuyo signo se obtienen estados inexistentes en la naturaleza y soluciones que contradicen la experiencia.
Según las soluciones de las ecuaciones de la mecánica cuántica y Hamilton-Jacoby, resulta que una partícula cargada en un campo magnético, además de girar en un círculo, también tiene vibraciones radiales-niveles de Landau (incluso en el caso de momento orbital nulo).
Durante estos 90 años, especialmente en experimentos de resonancia ciclotrónica muy precisos, ninguno ha detectado las vibraciones radiales de los electrones y los niveles de Landau.
Resolviendo esta ecuación, Schrödinger, al igual que Sommerfeld, obtuvo la fórmula (5), que describía la estructura del espectro del hidrógeno no exactamente. Además, de la solución del problema para una partícula en un pozo de potencial, resulta que una partícula con una longitud de onda ƛ=ℏ/mchas estados ligados (se coloca) en un pozo de tamaño arbitrario y, en particular, mucho menor que ƛ/2. Este hecho contradice el principio fundamental de la teoría cuántica (ondulatoria), el principio de incertidumbre.
En 1925 Schrödinger envió este trabajo a los editores de ‘Annalen der Physik’ , pero luego tomó el manuscrito, rechazó los planteamientos relativistas y en 1926 construyó una ecuación de onda basada en la expresión hamiltoniana clásica, la ecuación de Schrödinger .
La ecuación describía el espectro del átomo de hidrógeno sólo cualitativamente, sin embargo, no tenía restricciones irracionales ni soluciones singulares en la forma de la fórmula de Sommerfeld-Dirac. Klein , Fock y Gordon publicaron la ecuación relativista basada en la ecuación de onda para una partícula sin espín en 1926; se denomina ecuación de Klein-Fock-Gordon.
Con el descubrimiento del espín, la situación cambió drásticamente, y en 1926 Heisenberg y Jordan demostraron que, dentro de la descripción de Pauli del espín de un electrón, la mitad de la energía de la interacción espín-órbita es igual a un término con una potencia de α4 en la expansión en serie de Taylor de la ecuación de la fórmula de Sommerfeld la referencia va aquí.
Por qué exactamente la mitad, Thomas trató de explicar esto en 1927 por la presencia de una precesión relativista de un electrón en el marco de referencia de movimiento a lo largo de la órbita . La energía de la precesión de Thomas es exactamente igual a la mitad del valor de la energía de la interacción espín-órbita con el signo inverso (positivo), que debe sumarse a la energía de la interacción espín-órbita. Sin embargo, la suposición incorrecta de que la frecuencia de precesión de Thomas es idéntica en ambos marcos de referencia y la ausencia de una derivación común y correcta para los marcos de referencia no inerciales (en rotación) plantearon dudas sobre la corrección de tales planteamientos. La razón de la aparición de la mitad de la energía de la interacción espín-órbita en la fórmula de Sommerfeld sigue siendo objeto de investigación y es uno de los problemas no resueltos de la física moderna.
Por otra parte, tanto en la derivación de la fórmula de Sommerfeld como en la solución de la ecuación de Klein-Fock-Gordon para el problema del átomo de hidrógeno , no se tuvieron en cuenta inicialmente ni la energía de la interacción espín-órbita. Por lo tanto, el desdoblamiento fino obtenido no puede deberse en modo alguno a la interacción espín-órbita. Se trata de un efecto relativista pero puramente mecánico, cuando la masa (inercia) de una partícula ya depende de la velocidad de movimiento a lo largo de la órbita (del momento angular), por lo que el movimiento radial del electrón cambia, y viceversa. Justo esta dependencia, que da lugar a la división de los niveles de energía del electrón, y a la imposibilidad de introducir sólo uno, el número cuántico principal. Sin embargo, incluso con esta suposición, el orden de desdoblamiento de los niveles según la fórmula (8) contradice a la lógica; resulta que cuanto mayor es el momento angular orbital, menor es la energía del nivel desdoblado.
La representación matricial de la onda de segundo orden Ec. (9) mediante un sistema de ecuaciones de primer orden es la construcción de Dirac de la ecuación relativista del electrón (las matrices de Dirac son la representación particular de los números de Clifford-Lipschitz ). En la representación estándar la ecuación de Dirac para una partícula libre tiene la forma .
donde
son las matrices de Pauli (se omite la matriz unidad en las fórmulas).
Para una partícula en un campo externo, la Ec. (16) suele escribirse en la forma
donde para una representación invariante en el caso de una partícula libre, las ecuaciones se componen para la diferencia entre el momento generalizado y el momento del campo.
En el caso de la energía potencial de una carga inmóvil en un campo de Coulomb, obtenemos la fórmula de Sommerfeld-Dirac como resultado de una solución exacta de esta ecuación particular. También en este caso, aunque para un sistema con espín 1/2la energía de la interacción espín-órbita no se tiene en cuenta inicialmente, sino que la mitad se obtiene a partir de la solución exacta del problema del átomo de hidrógeno.
Mediciones más precisas de Lamb en 1947 y mejoras posteriores en el espectro del átomo de hidrógeno revelaron que, además de las líneas con el máximo j, todas las demás están también divididas y algo desplazadas (el desplazamiento de Lamb). Para armonizar los resultados de la teoría con los datos experimentales más precisos sobre el espectro del átomo de hidrógeno, había que proponer otras soluciones y enfoques que los establecidos por la derivación de la ecuación de Dirac.
Los nuevos enfoques teóricos no habían aportado nada y sólo complementaban la teoría con las propuestas ilógicas y no físicas para superar la singularidad emergente de las soluciones: la renormalización, la diferencia finita de infinitos con el valor deseado de la diferencia, etc. La contabilización del tamaño del núcleo corrigió sólo el valor Z en el valor mayor, pero no resolvió el problema Z>137. También se obtuvo un resultado increíble para el problema del átomo de hidrógeno de que el electrón se encuentra, muy probablemente, en el centro del átomo, es decir, en el núcleo.
Los resultados de la solución del problema para una partícula en un pozo de potencial tanto en el caso de la ecuación de Klein-Fock-Gordon como de la ecuación de Dirac contradicen al principio básico de la mecánica cuántica, al principio de incertidumbre. De las soluciones resulta que una partícula puede estar en un estado ligado en un pozo con cualquier dimensión, en particular, con el tamaño mucho menor que la longitud de onda de la propia partícula, A=ℏ/mc.
A pesar de que el propio Dirac propuso un sistema de ecuaciones relativistas lineales de primer grado en la representación matricial que describía el sistema con espín 1/2, las contradicciones no desaparecieron, y él mismo siguió descontento con los resultados de su teoría. Como escribió Dirac en 1956 , el desarrollo de la teoría relativista de los electrones puede considerarse ahora como un ejemplo de cómo los argumentos incorrectos conducen a veces a un resultado valioso. En los años 70 quedó claro que la teoría relativista de la mecánica cuántica no existe, y que hay que buscar nuevos enfoques y ecuaciones fundamentales para construir una teoría consistente de la mecánica cuántica relativista. Y en los años 80, Dirac ya hablaba de las dificultades insuperables de la teoría cuántica existente y de la necesidad de crear una nueva.
La razón del fracaso de estas teorías es bastante simple: está en el desconocimiento de la dependencia de la energía de interacción con el campo de la velocidad de la partícula. El momento generalizado del sistema, la partícula más el campo externo, es la suma de la expresión relativista para el momento mecánico de la partícula y el momento del campo en el caso de la interacción con la partícula inmóvil
que no es una representación invariante de la velocidad de la partícula. Para construir algún invariante a partir de dicha representación, se utilizó en todos los casos una relación «invariante» en forma de diferencia entre el momento generalizado del sistema y el momento del campo en el caso de la interacción con la partícula inmóvil
Obviamente, la permutación de las componentes del momento generalizado para la construcción del invariante no resuelve el problema planteado. La afirmación de que la expresión (20) es el momento mecánico de una partícula y, por tanto, es un invariante, no está demostrada y es necesario aprehender la fórmula (20) como empírica. Por lo tanto, a altas velocidades o a fuertes interacciones, no se tiene en cuenta la dependencia de la energía de la interacción de la partícula con el campo en la velocidad del movimiento de la partícula, lo que da lugar a resultados erróneos o a la imposibilidad de los cálculos.
En , se propuso una representación invariante del momento generalizado del sistema, donde se tuvo en cuenta la dependencia de la energía de interacción de la partícula con el campo en la velocidad:
que es la representación cuatridimensional del momento generalizado del sistema basada en la expresión del momento generalizado de una partícula inmóvil en estado de reposo
cuya invariante es siempre igual a la expresión (19) independientemente del estado del sistema.
La aplicación de los principios variacionales para construir la teoría relativista y cuántica se basó en los principios de construcción la mecánica con la ayuda de la Lagrangiana del sistema , que originalmente no estaba prevista para los enfoques relativistas. La construcción lagrangiana es paramétrica con una sola variable de tiempo τ = ct, destacada de las variables del espacio cuatridimensional (las demás están representadas por la dependencia de esta variable τ) y contiene la diferencial total con respecto a esta variable, la velocidad de la partícula. Tal construcción es inaceptable debido a la imposibilidad de aplicar el principio de invariancia de la representación de las variables y la representación covariante de la acción del sistema.
En , para construir la teoría relativista sobre la base de los principios variacionales, se han considerado las soluciones canónicas (no paramétricas) del problema variacional para las funciones integrales definidas canónicamente y se escriben las soluciones canónicas de los problemas variacionales de la mecánica en los espacios de Minkowski. Debido a la unificación de los principios variacionales de mínima acción, flujo e hiperflujo, se obtienen las ecuaciones canónicamente invariantes para el momento generalizado. A partir de estas ecuaciones, se obtienen las expresiones para la función de acción y la función de onda como solución general del problema variacional unificado de la mecánica.
A continuación presentamos el principio de invariancia generalizado y la correspondiente representación del momento generalizado del sistema, las ecuaciones de la mecánica relativista y cuántica , damos las soluciones de los problemas del movimiento de la carga en un campo eléctrico constante, los problemas para una partícula en un pozo de potencial y el paso de una partícula a través de una barrera de potencial, los problemas del movimiento en un campo exponencial (Morse), los problemas de la partícula cargada en un campo magnético, y también se dan los problemas de un átomo de hidrógeno.




