相対論的量子力学の方程式(スピンなし)
はじめに
-すべてを疑うこと、すべてを信じることは、同じように便利な二つの解決策である。
どちらも反射の必要性を省く。
Henri Poincaré (1854-1912)
分かっています。 – 5069>
Hypathia (∼360-415 AD)
1913年、ボーアはバルマーの経験式に基づき、軌道運動量の量子化に基づく原子のモデルを構築し、その後、より一般的なゾンマーフェルド量子化規則によって補足された。 5069>
1916年、ゾンマーフェルドは相対論的アプローチの枠組みの中で、スピンを考慮せずに水素型原子のエネルギー準位の公式を導いた。 ゾンマーフェルドはボーア原子のモデルから出発し、質量mの自由粒子の運動量とエネルギーEとの相対論的な関係を用いました。
四次元ポテンシャル(φ,A)の外場において、電荷qの粒子に対して、一般化した粒子の運動量の式から場の四次元運動量の成分(qφ、qA)を引くと、この関係も使えると考えられた:
E-qφ2pc-qA2=mc22.E2
クーロンポテンシャルφ=Ze/rの場合、eは電子の電荷、rは原子核からの距離、Zは原子番号で、球座標では
ここにLisは角運動量を表します。 Bohr-Sommerfeld量子化条件は
ここに、 nφ, nraはそれぞれ軌道量子数、動径量子数となる。 エネルギー準位については、Sommerfeldは
ここで主要量子数 n=nr+l+1=1,2,3,…, l=0,1,2,3,…,n-1, そして α=1/137.036 は微細構造定数と求めた。 しかし、1916年に発表された論文では、ゾンマーフェルドは「幸運な誤り」を犯し、導かれた式は次のような形で示された
式(6)は水素や他の類似原子のスペクトル構造のすべての特殊性と当時の測定精度の限界点を完全に表現し、式自体の正しさに疑いの余地はないものである。 そのため、Sommerfeld の公式は経験的なものとみなされ、量子数 l の代わりに、半整数の値 j=1/2,3/2,5/2,… を持つ「謎の」内部量子数が使われるようになったのです。n+1/2が導入され、式(6)を用いて
ここでn=nr+j+1/2=1,2,3,…,j=1/2,3/2,5/2,…、n+1/2とし、lはj=1/2で0、その他はl=j±1/2となるように表現された。 この式は、1928年にスピン1/2の粒子について相対論的Dirac方程式を厳密に解いた結果と、原子番号Zの原子核のクーロン場における不動電荷の位置エネルギーをUr=Ze2/rの形で表す古典的な式が一致します。
また式(7)には原子番号Z<137の原子核の電荷という奇妙な値の限界があり、それ以上になると式が意味をなさなくなっていることが指摘されています。 また、概説したアプローチの枠内では、強い相互作用、重力相互作用、惑星の運動が記述されないことも明らかにされた。 Z<137やα>1の問題は、相対論的量子力学の未解決の問題として残っている。 (7)式をテイラー級数で累乗Zα2の順に展開し、累乗Zα6の項まで正確に展開すると
1925-1926年にシュレーディンガーがドブロイ波を記述する粒子波動の方程式導出に取り組んだが、その際もこの方程式の導出が必要であったため、この方程式導出のためにSchlödingerは “Deuroglie波 “という概念を導入した。 この方程式の導出も、粒子の運動量とエネルギーEとの間の相対論的関係(1)に基づいて行われた。 これはエネルギーと運動量の2乗の演算子を用いて、波動関数
Sommerfeldと同様である。 シュレーディンガーは外場における粒子について次のような表現を用いた
aの静的状態の場合、外場にある粒子は、外場にある粒子と同じように、外場と同じように扱われます。 水素原子のクーロンポテンシャルの場における荷電粒子では、方程式
からわかるように、方程式を解く必要があったのです。 ポテンシャルエネルギーq2φ2r/2mc2の2次式が正の符号で式中に存在し、引き合う場の場合、解はある種の困難をもたらす。 特異点に近づくと、負の符号のために引力が増大し、特異点の存在によって相互作用の大きさに限界があることが知られている(図1)。
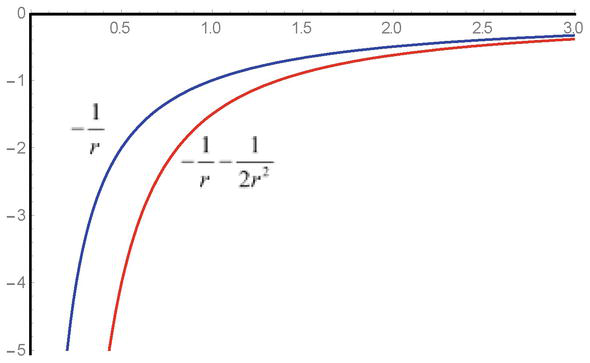
Figure 1.
クラインゴードン方程式の魅力場ポテンシャル1/rと潜在相互作用エネルギー1/r1/2r2におけるサンプルへの依存性を示す。
次に、波動ベクトルkは
そしてエネルギーEthの粒子を、ポテンシャル障壁U=qφr(図2)を通過するという問題を考えるとき、次のように表される。 高さが粒子の静止エネルギーの2倍U>2mc2より大きい場合、透過係数は障壁の高さに関係なく1になってしまう(クラインのパラドックス) ……。
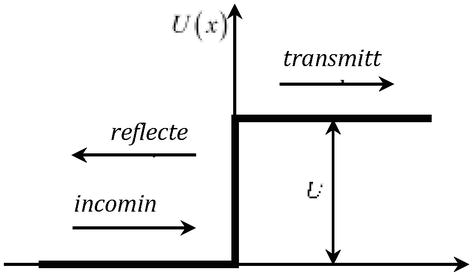
図2.
ポテンシャル障壁を通過する粒子の通過U.
もう一つの困難は、ポテンシャル井戸の粒子問題の解が示すように、十分な深さがあれば、波長ƛ=ℏ/mccの粒子は粒子の波長d<ƛ/2より狭い井戸幅で境界状態を持てる(局在できる)(図3)、量子力学の基本原理-ハイゼンベルグの不確かさの原理に矛盾していることである。
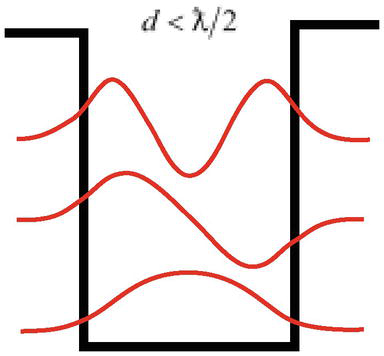
Figure 3.
波長ƛの粒子は幅d<ƛ/2の井戸に局在することができる。
また、水素型原子の問題の解は、原子核の序数Z≦68(Dirac方程式では、原子番号の制約はZ≦137)の値で制限される。 相対論的力学でも同様で、強い相互作用を考える場合、ハミルトン-ヤコビ相対論方程式の解はいわゆる「粒子の中心への落下」を示す。
2次項の除去または符号の反転のため、近年、クライン-ゴードン方程式やディラック方程式のポテンシャルエネルギーをスカラーとベクトルのポテンシャル表現からの2乗の差で表すことが提案されている(S波方程式)。 このような数学的形式は状況を正すものであるが、物理学的な観点からはこのような表現は正当化されず、このような擬ポテンシャルに対応する場は自然界には存在しない。
ベクトル場の2次項の存在によって事態はさらに悪化し、その符号のために自然界に存在しない状態や経験に矛盾する解が得られている。
量子力学とハミルトンジャコビーの方程式の解によれば、量子力学とハミルトンジャコビーの方程式の答えは、次のようになります。 磁場中の荷電粒子は、円周上を回転するだけでなく、半径方向の振動-ランダウ準位を持つことが判明した(軌道運動量がゼロの場合も)。
この90年間、特に非常に正確なサイクロトロン共鳴実験において、誰も電子半径振動とランダウ準位を検出したことはありません。
この方程式を解いて、シュレーディンガーはゾンマーフェルドと同様に式(5)を得ましたが、これは水素スペクトルの構造を正確に記述するものではありませんでした。 さらに、ポテンシャル井戸の中の粒子の問題を解くと、波長ƛ=ℏ/mchas の粒子は、任意の大きさの、特にƛ/2 よりはるかに小さい井戸に結合状態を持つ(置かれる)ことが判明した。 この事実は、量子(波動)理論の基本原理である不確定性原理に反する。
1925年にシュレーディンガーはこの仕事を「Annalen der Physik」の編集者に送ったが、その後原稿を受け取り、相対論的アプローチを拒否して、1926年に古典ハミルトン式、シュレーディンガー方程式を基に波動方程式を構築した … 続きを読む
方程式は水素原子のスペクトルを定性的にだけ記述しますが、無理な制限やSommerfeld-Dirac式の形の特異解を持ってはいませんでした。 クライン、フォック、ゴードンは1926年にスピンのない粒子の波動方程式に基づく相対論的方程式を発表し、クライン-フォック-ゴードン方程式と呼ばれる。
スピンの発見で状況は一変し、1926年にハイゼンベルグとジョーダンは電子のスピンのパウリ記述においてスピン軌道相互作用のエネルギーの半分が、Sommerfeld方程式のテイラー級数展開におけるα4乗に相当する項があることを示した参照はこちら。
なぜ正確に半分かというと、トーマスは1927年にこれを軌道に沿った運動の基準フレームにおける電子の相対論的歳差運動の存在によって説明しようとした 。 トーマス歳差運動のエネルギーは、スピン軌道相互作用のエネルギーに逆符号(正符号)を加えた値のちょうど半分に等しく、スピン軌道相互作用のエネルギーに加えるべきものである。 しかし、トーマス歳差周波数はどちらの参照枠でも同じであるという誤った仮定や、非慣性(回転)参照枠に対する共通で正しい導出がないことから、このようなアプローチの正しさに疑問が持たれていました。 一方、ゾンマーフェルトの公式の導出や水素原子問題のクライン-フォック-ゴードン方程式の解法では、スピンやスピン軌道相互作用のエネルギーは考慮されていないため、ゾンマーフェルトの公式がスピン軌道相互作用のエネルギーの半分を含む理由はまだ調査中で、現代物理学の未解決問題の1つとなっています
一方、水素原子問題のクライン・フォック-ゴードン方程式では、最初にスピンが考慮され、また、スピン-フォックのエネルギーは、スピン-ゴードン方程式の導出の際に考慮されました。 したがって、得られた微細な分裂は、決してスピン軌道相互作用に起因するものではありません。 これは、粒子の質量(慣性)がすでに軌道に沿った運動速度(角運動量)に依存しており、そのために電子の半径方向の運動が変化し、またその逆も起こるという相対論的ではあるが純粋に力学的な効果である。 この依存性によって、電子のエネルギー準位が分裂し、主量子数を1つだけ導入することが不可能になるのである。 しかし、この仮定でも、式(8)による準位の分裂の順序は論理に反し、軌道角運動量が大きいほど分裂した準位のエネルギーは小さくなることがわかる。 (9)を1次方程式系で行列表現すると、相対論的電子方程式のDirac構成になる(Dirac行列はClifford-Lipschitz数の特殊な表現である)。 標準的な表現では、自由粒子に対する Dirac 方程式は次のような形になります .
ここで
はPuli行列(式中の単位行列は省略)です。
外場中の粒子に対して、式(1)は (16)は通常
ここで、自由粒子の場合の不変表現では、一般化運動量と場の運動量の差について方程式が構成される。
クーロン場における不動電荷の位置エネルギーの場合、この特殊な方程式を厳密に解いた結果、Sommerfeld-Diracの式が得られます。 そこでも、スピン1/2の系ではスピン軌道相互作用のエネルギーは当初考慮されないが、水素原子の問題の厳密解から半分が得られる。
1947年にラムの測定がより正確になり、その後水素原子のスペクトルが改良されて、最大jの線に加えて、他のすべての線も分裂して多少ずれている(ラムシフト)ことが判明した。 5069>
新しい理論的アプローチは何も生み出さず、解の特異性を克服するために、繰り込み、無限大の有限差とその差の望ましい値など、非論理的で非物理的な提案で理論を補うだけであった。 原子核の大きさを考慮すると、Z値が大きく補正されるだけで、Z>137問題は解けなかった。
ポテンシャル井戸の中の粒子の問題を、クライン・フォック・ゴルドン方程式とディラック方程式の両方で解いた結果は、量子力学の基本原理である不確定性原理と矛盾するものであった。 解答から、粒子は任意の次元、特に粒子自身の波長A=ℏ/mcよりはるかに小さいサイズの井戸の中で束縛状態になりうることが判明した。
ディラック自身、スピン1/2の系を記述する行列表現による線形1次相対論方程式系を提案したにもかかわらず、矛盾は解消されず、彼自身、自分の理論の結果に不満を持ったままでした。 ディラックが1956年に書いたように、相対論的電子論の発展は、誤った議論が時に貴重な結果をもたらす例として考えられるようになった。 70年代に入ると、相対論的量子力学の理論が存在しないことが明らかになり、相対論的量子力学の一貫した理論を構築するために、新たな基礎的アプローチと方程式を模索することになる。 80 年代には、ディラックがすでに、既存の量子論の克服しがたい困難さと新しい量子論の必要性を語っています
これらの理論の失敗の理由は非常に単純です。 粒子+外場の系の一般化された運動量は、粒子の力学的運動量の相対論的表現と不動粒子との相互作用の場合の場の運動量の和
これは粒子速度の不変表現ではないのである。 このような表現から何らかの不変量を構成するために、不動粒子との相互作用の場合
明らかに、不変量の構築のための一般化運動量の成分の順列は、提起された問題を解決しない。 式(20)は粒子の力学的運動量だから不変量であるというのは証明されておらず、式(20)を経験的に理解することが必要である。 そのため、高速度や強い相互作用がある場合、粒子と場の相互作用のエネルギーが粒子の運動速度に依存することが説明できず、誤った結果や計算が不可能になることがある。
では、一般化された系の運動量の不変表現を提案し、粒子と場の相互作用エネルギーの速度依存性を考慮した。
これは、静止状態の不動粒子の一般化運動量の式
に基づいて系の一般化運動量を4次元で表したもので、系の状態にかかわらず不変量は常に式(19)に等しくなる。
相対論や量子論の構築に変分原理を適用したのは、本来相対論的なアプローチを意図していなかった系のラグランジアンを用いて力学を構築する原理に基づいている。 ラグランジアンの構築は、4次元空間の変数から切り離された1つの時間変数τ = ctをパラメトリックに用い(残りはこの変数τへの依存で表される)、この変数に関する全微分、粒子の速度が含まれる。
変分原理に基づいて相対論的理論を構築するために、正準定義積分関数に対する変分問題の正準解(ノンパラメトリック)を考察し、ミンコフスキー空間における力学の変分問題の正準解を記述した。 最小作用、フロー、ハイパーフローの変分原理を統一することにより、一般化運動量に対する正準不変方程式が得られる。 これらの式から、作用関数と波動関数の式が、力学の統一変分問題の一般解として得られる。
以下、一般化不変性原理とそれに対応する系の一般化運動量の表現、相対論的・量子力学の方程式を示し、一定電場中の電荷運動の問題、ポテンシャル井戸中の粒子の問題、ポテンシャル障壁を通る粒子の問題、指数場(モース)中の運動の問題、磁場中の荷電粒子の問題、さらに水素原子の問題の解を与えている
以下は、一般化不変性原理の説明と一般化運動量の表現の説明、相対論と量子力の方程式を示 している。




