Ecuațiile mecanicii relativiste și cuantice (fără spin)
Introducere
-Să te îndoiești de tot sau să crezi totul sunt două soluții la fel de convenabile;
ambele renunță la necesitatea reflecției.
Henri Poincaré (1854-1912)
Știu, știu, dar să presupunem – doar să presupunem! – puritatea cercului ne-a orbit să vedem ceva dincolo de el!
Trebuie să o iau de la capăt cu alți ochi, trebuie să regândesc totul!
Hypathia (∼360-415 d.Hr.)
În 1913, Bohr, pe baza formulelor empirice ale lui Balmer, a construit un model de atom bazat pe cuantificarea momentului orbital , care a fost completat ulterior de regulile mai generale de cuantificare ale lui Sommerfeld. În acei ani, în mod firesc, nu s-a presupus prezența unui spin sau a unui moment magnetic intrinsec al particulei sau, mai ales, a interacțiunii spin-orbită, sau a interacțiunii cu spinul nuclear.
În 1916, Sommerfeld, în cadrul abordărilor relativiste, a derivat o formulă pentru nivelurile energetice ale unui atom de tip hidrogen, fără a lua în considerare spinul . Sommerfeld a pornit de la modelul atomului Bohr și a folosit relația relativistă dintre momentul pand energia E a unei particule libere cu masa m.
unde cis viteza luminii.
Într-un câmp exterior cu un potențial cvadridimensional (φ,A), s-a presupus că pentru o particulă cu sarcina qaceastă relație poate fi de asemenea folosită dacă scădem componentele momentului cvadridimensional al câmpului (qφ,qA) din expresia momentului generalizat al particulei:
În cazul potențialului Coulomb φ=Ze/r, unde e este sarcina electronului, ris distanța față de nucleu, iar Zeste un număr atomic, obținem în coordonate sferice
unde Lis este momentul unghiular. Condițiile de cuantificare Bohr-Sommerfeld iau forma
unde nφși nrare numerele cuantice orbitale și, respectiv, radiale. Pentru nivelurile de energie, Sommerfeld a obținut formula
unde numărul cuantic principal n=nr+l+1=1,2,3,…, l=0,1,2,3,…,n-1, iar α=1/137,036este constanta structurii fine. Cu toate acestea, într-o lucrare publicată în 1916 , Sommerfeld „a făcut o greșeală norocoasă” și formula derivată a fost prezentată sub următoarea formă
Formula (6) descria perfect toate particularitățile structurii spectrului hidrogenului și al altor atomi similari, cu precizia limită pentru acei ani a măsurătorilor, și nu exista nici o îndoială asupra corectitudinii formulei în sine. Prin urmare, formula lui Sommerfeld a fost percepută ca fiind empirică, iar în locul numărului cuantic l, un „misterios” număr cuantic intern cu valori semiintegrale j=1/2,3/2,3/2,5/2,…,n+1/2a fost introdusă formula (6), iar formula (6) a fost utilizată în reprezentarea
unde n=nr+j+1/2=1,2,3,…,j=1/2,3/2,5/2,…,n+1/2, iar l posedă valorile l=0 la j=1/2și l=j±1/2pentru celelalte. Această formulă coincide cu rezultatul rezolvării exacte a ecuațiilor relativiste ale lui Dirac în 1928 pentru o particulă cu spinul 1/2cu expresia clasică pentru energia potențială a unei sarcini imobile în câmpul Coulomb al unui nucleu cu numărul atomic Zîn forma Ur=Ze2/r.
Formula (7) a indicat, de asemenea, o limitare ciudată a valorii sarcinii unui nucleu cu numărul atomic Z<137, peste care formula își pierde sensul. De asemenea, a fost evident că în cadrul abordărilor prezentate, interacțiunile puternice și gravitaționale, mișcările planetelor nu sunt descrise. Problema Z<137sau α>1 rămâne o problemă nerezolvată a mecanicii cuantice relativiste. Dezvoltând formula (7) pe ordinul puterilor Zα2în seria Taylor, cu o precizie a expansiunii până la termenii cu puteri Zα6, se obține
În 1925-1926, Schrödinger a lucrat la derivarea ecuației pentru funcția de undă a unei particule care descrie undele lui De Broglie . Derivarea ecuației s-a bazat, de asemenea, pe relația relativistă (1) dintre momentul pand energia Ea particulei, pe care a prezentat-o cu ajutorul operatorilor pătratelor energiei și impulsului sub forma unei ecuații pentru funcția de undă
Ca Sommerfeld, Schrödinger a folosit următoarea reprezentare pentru o particulă într-un câmp exterior
În cazul stărilor staționare ale unui particule încărcate în câmpul potențialului Coulomb pentru un atom de hidrogen a fost necesară rezolvarea ecuației
Cum se poate observa, expresia pătratică a energiei potențiale q2φ2r/2mc2este prezentă în ecuație cu semn pozitiv, iar în cazul unor câmpuri atrăgătoare, soluțiile conduc la anumite dificultăți. Atunci când ne apropiem de punctul de singularitate, datorită semnului negativ, forțele de atracție cresc, iar prezența singularității conduce la limitări cunoscute ale mărimii interacțiunilor (figura 1).
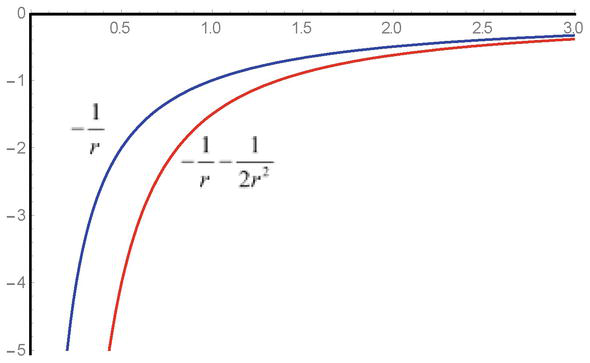
Figura 1.
Dependența de probă a potențialului câmpului atractiv-1/și a energiei potențiale de interacțiune-1/r-1/2r2din ecuațiile Klein-Gordon.
În continuare, vectorul de undă keste reprezentat ca
și atunci când se consideră problema trecerii unei particule cu energia Ethprintr-o barieră de potențial U=qφr(figura 2), a cărei înălțime este mai mare decât energia de repaus dublată a particulei U>2mc2, coeficientul de transmisie devine unitate, indiferent de înălțimea barierei (paradoxul Klein) .
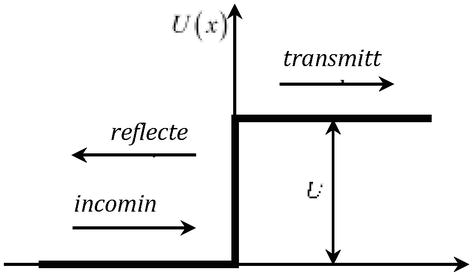
Figura 2.
Pasajul unei particule printr-o barieră de potențialU.
O altă dificultate este că, așa cum arată soluția problemei particulelor într-un puț de potențial, la o adâncime suficientă, o particulă cu lungimea de undă ƛ=ℏ/mc poate avea stări legate (poate fi localizată) într-o lățime a puțului mai mică decât lungimea de undă a particulei d<ƛ/2(figura 3), ceea ce contrazice principiul fundamental al mecanicii cuantice – principiul de incertitudine al lui Heisenberg.
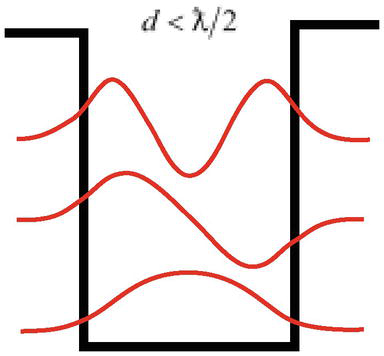
Figura 3.
O particulă cu o lungime de undăƛpoate fi localizată într-o lățime de puțd<ƛ/2.
De asemenea, rezolvarea problemei unui atom asemănător hidrogenului este limitată de valoarea numărului ordinal al nucleului atomic Z≤68(pentru ecuația Dirac, restricția numărului atomic este Z≤137). Același lucru în mecanica relativistă – atunci când se iau în considerare interacțiunile puternice, soluția ecuației relativiste Hamilton-Jacoby indică așa-numita „cădere a particulelor pe centru” .
Pentru a scăpa de termenul pătratic sau pentru a-i inversa semnul, în ultimii ani s-a propus reprezentarea energiei potențiale în ecuațiile Klein-Gordon și Dirac ca diferență de pătrate din expresiile potențialelor scalare și vectoriale (ecuația undelor S) . Un astfel de formalism matematic corectează situația, dar din punct de vedere fizic astfel de reprezentări nu se justifică în nici un fel, iar câmpurile corespunzătoare unor astfel de pseudo-potențiali nu există în natură.
Lucrurile stau și mai rău în cazul prezenței unui termen pătratic al câmpului vectorial, din cauza semnului căruia se obțin stări inexistente în natură și soluții care contrazic experiența.
Conform soluțiilor ecuațiilor din mecanica cuantică și Hamilton-Jacoby, se dovedește că o particulă încărcată într-un câmp magnetic, pe lângă faptul că se rotește în cerc, are și vibrații radiale-niveluri Landau (chiar și în cazul unui moment orbital zero).
În acești 90 de ani, în special în experimente de rezonanță ciclotronică foarte precise, nimeni nu a detectat vibrațiile radiale ale electronilor și nivelurile Landau.
Rezolvând această ecuație, Schrödinger, ca și Sommerfeld, a obținut formula (5), care descria nu exact structura spectrului de hidrogen. Mai mult, din rezolvarea problemei pentru o particulă într-un puț de potențial, rezultă că o particulă cu o lungime de undă ƛ=ℏ/mchas bound states (este plasată) într-un puț de mărime arbitrară și, în special, mult mai mică decât ƛ/2. Acest fapt contrazice principiul fundamental al teoriei cuantice (ondulatorii), principiul incertitudinii.
În 1925 Schrödinger a trimis această lucrare editorilor de la ‘Annalen der Physik’ , dar apoi a luat manuscrisul, a refuzat abordările relativiste și în 1926 a construit o ecuație ondulatorie bazată pe expresia hamiltoniană clasică, ecuația lui Schrödinger .
Ecuația descria spectrul atomului de hidrogen doar calitativ, însă nu avea restricții nerezonabile sau soluții singulare sub forma formulei Sommerfeld-Dirac. Klein , Fock și Gordon au publicat ecuația relativistă bazată pe ecuația de undă pentru o particulă fără spin în 1926; se numește ecuația Klein-Fock-Gordon.
Cu descoperirea spinului, situația s-a schimbat radical, iar în 1926 Heisenberg și Jordan au arătat că, în cadrul descrierii Pauli a spinului unui electron, jumătate din energia interacțiunii spin-orbită este egală cu un termen cu o putere de α4 în expansiunea în serie Taylor a ecuației formulei Sommerfeld referința ecuației merge aici.
De ce exact jumătate, Thomas a încercat să explice acest lucru în 1927 prin prezența unei precesii relativiste a unui electron în cadrul de referință al mișcării de-a lungul orbitei . Energia precesiei lui Thomas este exact egală cu jumătate din valoarea energiei interacțiunii spin-orbită cu semnul invers (pozitiv), care ar trebui să se adauge la energia interacțiunii spin-orbită. Cu toate acestea, presupunerea incorectă că frecvența de precesie Thomas este identică în ambele cadre de referință și absența unei derivări comune și corecte pentru cadrele de referință non-inerțiale (rotative) au ridicat îndoieli cu privire la corectitudinea unor astfel de abordări. Motivul apariției a jumătate din energia interacțiunii spin-orbită în formula Sommerfeld este încă în curs de investigare și este una dintre problemele nerezolvate în fizica modernă.
Pe de altă parte, atât la derivarea formulei Sommerfeld, cât și la rezolvarea ecuației Klein-Fock-Gordon pentru problema atomului de hidrogen , nici spinul, nici energia interacțiunii spin-orbită nu au fost luate în considerare inițial. Prin urmare, divizarea fină obținută nu se poate datora în niciun caz interacțiunii spin-orbită. Acesta este un efect relativist, dar pur mecanic, atunci când masa (inerția) unei particule depinde deja de viteza de mișcare de-a lungul orbitei (a momentului unghiular), din cauza căreia se modifică mișcarea radială a electronului și invers. Tocmai această dependență, care duce la divizarea nivelurilor energetice ale electronului și la imposibilitatea introducerii unui singur număr cuantic principal, numărul cuantic principal. Cu toate acestea, chiar și cu această ipoteză, ordinea de scindare a nivelurilor conform formulei (8) contrazice logica; se dovedește că, cu cât momentul unghiular orbital este mai mare, cu atât mai mică este energia nivelului scindat.
Reprezentarea matriceală a undei de ordinul doi Ec. (9) printr-un sistem de ecuații de ordinul întâi este construcția Dirac a ecuației relativiste a electronului (matricile Dirac sunt reprezentarea particulară a numerelor Clifford-Lipschitz ). În reprezentarea standard, ecuația Dirac pentru o particulă liberă are forma .
unde
sunt matricile Pauli (în formule se omite matricea unitate).
Pentru o particulă aflată într-un câmp exterior, Ec. (16) se scrie de obicei sub forma
unde, pentru o reprezentare invariantă în cazul unei particule libere, ecuațiile sunt compuse pentru diferența dintre momentul generalizat și momentul câmpului.
În cazul energiei potențiale a unei sarcini imobile într-un câmp Coulomb, se obține formula Sommerfeld-Dirac ca rezultat al unei soluții exacte a acestei ecuații particulare. Acolo, din nou, deși pentru un sistem cu spin 1/2energia interacțiunii spin-orbită nu este luată în considerare inițial, ci jumătatea este obținută din soluția exactă a problemei atomului de hidrogen.
Măsurătorile mai precise ale lui Lamb din 1947 și îmbunătățirile ulterioare ale spectrului atomului de hidrogen au arătat că, pe lângă liniile cu maximul j, toate celelalte sunt, de asemenea, divizate și oarecum deplasate (deplasarea Lamb). Pentru a armoniza rezultatele teoriei cu datele experimentale mai precise privind spectrul atomului de hidrogen, a trebuit să se propună alte soluții și abordări decât cele stabilite prin derivarea ecuației lui Dirac.
Noile abordări teoretice nu au dat nimic și doar au completat teoria cu propuneri ilogice și nefizice pentru a depăși singularitatea emergentă a soluțiilor: renormalizarea, diferența finită a infiniturilor cu valoarea dorită a diferenței, și așa mai departe. Luarea în considerare a dimensiunii nucleului a corectat doar valoarea Z în valoare mai mare, dar nu a rezolvat problema Z>137. Un rezultat incredibil a fost obținut și pentru problema atomului de hidrogen, conform căruia electronul se află, cel mai probabil, în centrul atomului, adică în nucleu.
Rezultatele rezolvării problemei pentru o particulă într-un puț de potențial, atât în cazul ecuației Klein-Fock-Gordon, cât și în cazul ecuației Dirac, sunt în contradicție cu principiul de bază al mecanicii cuantice, cu principiul incertitudinii. Din soluții reiese că o particulă se poate afla într-o stare legată într-un puț cu orice dimensiuni, în special cu dimensiunea mult mai mică decât lungimea de undă a particulei însăși, A=ℏ/mc.
În ciuda faptului că Dirac însuși a propus un sistem de ecuații relativiste liniare de gradul întâi în reprezentarea matriceală care descria sistemul cu spin 1/2, contradicțiile nu au dispărut, iar el însuși a rămas nemulțumit de rezultatele teoriei sale. După cum scria Dirac în 1956 , dezvoltarea teoriei relativiste a electronilor poate fi considerată acum ca un exemplu al modului în care argumentele incorecte conduc uneori la un rezultat valoros. În anii ’70, a devenit clar că teoria relativistă a mecanicii cuantice nu există și că trebuie căutate abordări și ecuații noi, fundamentale, pentru a construi o teorie coerentă a mecanicii cuantice relativiste. Iar în anii ’80, Dirac vorbea deja despre dificultățile insurmontabile ale teoriei cuantice existente și despre necesitatea de a crea una nouă.
Motivul eșecului acestor teorii este destul de simplu – se află în ignorarea dependenței energiei de interacțiune cu câmpul de viteza particulei. Momentul generalizat al sistemului, particula plus câmpul exterior, este suma expresiei relativiste a momentului mecanic al particulei și a momentului câmpului în cazul interacțiunii cu particula imobilă
care nu este o reprezentare invariantă a vitezei particulei. Pentru a construi un oarecare invariant dintr-o astfel de reprezentare, s-a folosit în toate cazurile o relație „invariantă” sub forma unei diferențe între momentul generalizat al sistemului și momentul de câmp în cazul interacțiunii cu particula imobilă
Evident, permutarea componentelor momentului generalizat pentru construcția invarianților nu rezolvă problema pusă. Afirmația că expresia (20) este momentul mecanic al unei particule și deci este un invariant nu este demonstrată și este necesar să se aprecieze formula (20) ca fiind una empirică. Prin urmare, la viteze mari sau la interacțiuni puternice, se produce o dependență inexplicabilă a energiei de interacțiune a particulei cu câmpul de viteza de mișcare a particulei, ceea ce duce la rezultate eronate sau la imposibilitatea efectuării calculelor.
În , a fost propusă o reprezentare invariantă a momentului generalizat al sistemului, în care a fost luată în considerare dependența energiei de interacțiune a particulei cu câmpul de viteza:
care este reprezentarea cvadridimensională a momentului generalizat al sistemului bazată pe expresia pentru momentul generalizat al unei particule imobile în stare de repaus
al cărei invariant este întotdeauna egal cu expresia (19) indiferent de starea sistemului.
Aplicarea principiilor variaționale pentru a construi teoria relativistă și cuantică s-a bazat pe principiile de construcție a mecanicii cu ajutorul Lagrangianului sistemului , care inițial nu era destinat abordărilor relativiste. Construcția lagrangiană este parametrizată cu o singură variabilă de timp τ = ct, singularizată dintre variabilele spațiului cvadridimensional (restul sunt reprezentate prin dependența de această variabilă τ) și conține diferențiala totală în raport cu această variabilă, viteza particulei. O astfel de construcție este inacceptabilă din cauza imposibilității de a aplica principiul invarianței reprezentării variabilelor și a reprezentării covariante a acțiunii sistemului.
În , pentru a construi teoria relativistă pe baza principiilor variaționale, s-au considerat soluțiile canonice (neparametrice) ale problemei variaționale pentru funcționale integrale definite canonic și s-au scris soluțiile canonice ale problemelor variaționale ale mecanicii în spațiile Minkowski. Datorită unificării principiilor variaționale ale acțiunii minime, fluxului și hiperfluxului, se obțin ecuațiile invariante canonice pentru impulsul generalizat. Din aceste ecuații se obțin expresiile pentru funcția de acțiune și funcția de undă ca soluție generală a problemei variaționale unificate a mecanicii.
În continuare, prezentăm principiul invarianței generalizate și reprezentarea corespunzătoare a momentului generalizat al sistemului, ecuațiile mecanicii relativiste și cuantice , dăm soluțiile problemelor de mișcare a sarcinii într-un câmp electric constant, problemele pentru o particulă într-un puț de potențial și trecerea unei particule printr-o barieră de potențial, problemele de mișcare într-un câmp exponențial (Morse), problemele particulei încărcate într-un câmp magnetic și, de asemenea, sunt date problemele unui atom de hidrogen.
.




