Equazioni di Meccanica Relativistica e Quantistica (senza Spin)
Introduzione
-Debitare tutto o credere tutto sono due soluzioni ugualmente convenienti;
entrambe dispensano dalla necessità della riflessione.
Henri Poincaré (1854-1912)
Lo so, lo so, ma supponiamo – solo supponiamo! – che la purezza del cerchio ci abbia impedito di vedere qualcosa al di là di esso!
Devo ricominciare tutto da capo con occhi nuovi, devo ripensare tutto!
Hypathia (∼360-415 d.C.)
Nel 1913, Bohr, basandosi sulle formule empiriche di Balmer, costruì un modello di atomo basato sulla quantizzazione del momento orbitale, che fu successivamente integrato dalle più generali regole di quantizzazione di Sommerfeld. In quegli anni, naturalmente, la presenza di uno spin o di un momento magnetico intrinseco della particella o, soprattutto, l’interazione spin-orbita, o l’interazione con lo spin nucleare, non era supposta.
Nel 1916, Sommerfeld, nel quadro degli approcci relativistici, derivò una formula per i livelli di energia di un atomo simile all’idrogeno, senza tener conto dello spin. Sommerfeld procedeva dal modello dell’atomo di Bohr e utilizzava la relazione relativistica tra la quantità di moto e l’energia E di una particella libera di massa m.
dove c è la velocità della luce.
In un campo esterno con un potenziale quadridimensionale (φ,A), si è supposto che per una particella con la carica q questa relazione può anche essere usata se si sottraggono le componenti del momento quadridimensionale del campo (qφ,qA) dall’espressione per il momento generalizzato della particella:
Nel caso del potenziale di Coulomb φ=Ze/r, dove e è la carica dell’elettrone, ris la distanza dal nucleo, e Z è un numero atomico, si ottiene in coordinate sferiche
dove Lis il momento angolare. Le condizioni di quantizzazione di Bohr-Sommerfeld hanno la forma
dove nφ e nrare i numeri quantici orbitali e radiali, rispettivamente. Per i livelli energetici, Sommerfeld ottenne la formula
dove il numero quantico principale n=nr+l+1=1,2,3,…, l=0,1,2,3,…,n-1, e α=1/137,036 è la costante di struttura fine. Tuttavia, in un articolo pubblicato nel 1916, Sommerfeld “fece un errore fortunato” e la formula derivata fu presentata nella seguente forma
La formula (6) descriveva perfettamente tutte le peculiarità della struttura dello spettro dell’idrogeno e di altri atomi simili con la precisione limitante per quegli anni delle misure, e non vi erano dubbi sulla correttezza della formula stessa. Pertanto, la formula di Sommerfeld fu percepita come empirica, e al posto del numero quantico l, un ‘misterioso’ numero quantico interno con valori semintegrali j=1/2,3/2,5/2,…,n+1/2 è stato introdotto, e la formula (6) è stata usata nella rappresentazione
dove n=nr+j+1/2=1,2,3,…,j=1/2,3/2,5/2,…,n+1/2, e l possiede i valori l=0 a j=1/2 e l=j±1/2 per gli altri. Questa formula coincide con il risultato di una soluzione esatta delle equazioni relativistiche di Dirac nel 1928 per una particella con lo spin 1/2 con l’espressione classica per l’energia potenziale di una carica immobile nel campo di Coulomb di un nucleo con un numero atomico Z nella forma Ur=Ze2/r.
La formula (7) indicava anche una strana limitazione di valore della carica di un nucleo con il numero atomico Z<137, oltre la quale la formula perde il suo significato. Era anche evidente che nel quadro degli approcci delineati, le interazioni forti e gravitazionali, i moti dei pianeti non sono descritti. Il problema Z<137 o α>1 rimane il problema irrisolto della meccanica quantistica relativistica. Espandendo la formula (7) sull’ordine delle potenze Zα2 nella serie di Taylor, con una precisione di espansione fino ai termini per le potenze Zα6, si ottiene
Nel 1925-1926, Schrödinger lavorò alla derivazione dell’equazione della funzione d’onda di una particella che descrive le onde di De Broglie. La derivazione dell’equazione si basava anche sulla relazione relativistica (1) tra la quantità di moto e l’energia E della particella, che egli presentò con l’aiuto degli operatori dei quadrati dell’energia e della quantità di moto sotto forma di un’equazione per la funzione d’onda
come Sommerfeld, Schrödinger usò la seguente rappresentazione per una particella in un campo esterno
Nel caso di stati stazionari di una particella carica nel campo del potenziale di Coulomb per un atomo di idrogeno è stato necessario risolvere l’equazione
Come si vede, l’espressione quadratica dell’energia potenziale q2φ2r/2mc2è presente nell’equazione con un segno positivo e nel caso di campi attrattivi, le soluzioni portano ad alcune difficoltà. Quando ci si avvicina al punto di singolarità, a causa del segno negativo, le forze attrattive aumentano e la presenza della singolarità porta alle note limitazioni sulla grandezza delle interazioni (Figura 1).
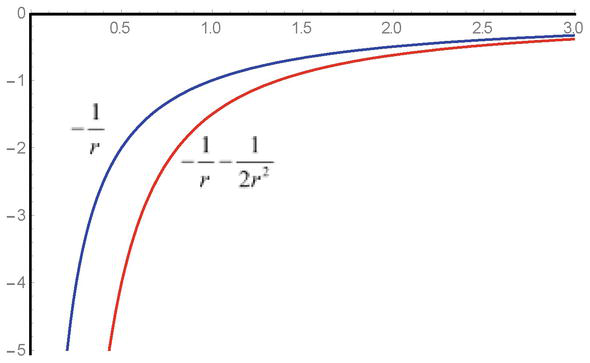
Figura 1.
La dipendenza dal campione del potenziale del campo attrattivo-1/ed energia di interazione potenziale-1/r-1/2r2 nelle equazioni di Klein-Gordon.
Poi, il vettore d’onda k è rappresentato come
e quando si considera il problema del passaggio di una particella con energia Ethrough una barriera potenziale U=qφr(Figura 2), la cui altezza è maggiore dell’energia di riposo raddoppiata della particella U>2mc2, il coefficiente di trasmissione diventa unitario, indipendentemente dall’altezza della barriera (paradosso di Klein).
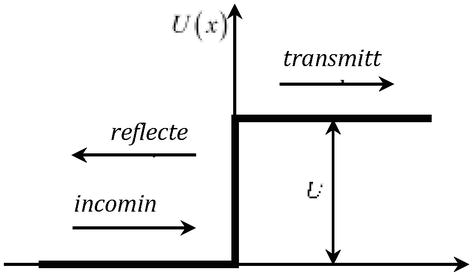
Figura 2.
Passaggio di una particella attraverso una barriera potenzialeU.
Un’altra difficoltà è che, come mostra la soluzione del problema delle particelle in un pozzo di potenziale, ad una profondità sufficiente, una particella con una lunghezza d’onda ƛ=ℏ/mcc può avere stati legati (può essere localizzata) in una larghezza del pozzo più stretta della lunghezza d’onda della particella d<ƛ/2 (Figura 3), il che contraddice il principio fondamentale della meccanica quantistica, il principio di indeterminazione di Heisenberg.
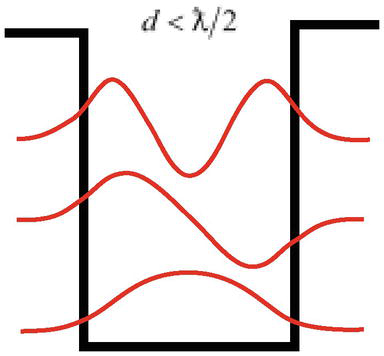
Figura 3.
Una particella con una lunghezza d’ondaƛpuò essere localizzata in un pozzo di larghezzad<ƛ/2.
Anche la soluzione del problema di un atomo simile all’idrogeno è limitata dal valore del numero ordinale del nucleo atomico Z≤68 (per l’equazione di Dirac, la restrizione del numero atomico è Z≤137). Lo stesso in meccanica relativistica – quando si considerano le interazioni forti, la soluzione dell’equazione relativistica di Hamilton-Jacoby indica la cosiddetta “caduta della particella sul centro”.
Per liberarsi del termine quadratico o invertire il suo segno, negli ultimi anni è stato proposto di rappresentare l’energia potenziale nelle equazioni di Klein-Gordon e Dirac come la differenza dei quadrati delle espressioni dei potenziali scalari e vettoriali (equazione delle onde S). Tale formalismo matematico corregge la situazione, ma da un punto di vista fisico tali rappresentazioni non sono in alcun modo giustificate, e i campi corrispondenti a tali pseudo-potenziali non esistono in natura.
Le cose sono ancora peggio con la presenza di un termine quadratico del campo vettoriale, a causa del cui segno si ottengono stati inesistenti in natura e soluzioni che contraddicono l’esperienza.
In base alle soluzioni delle equazioni della meccanica quantistica e di Hamilton-Jacoby, si scopre che una particella carica in un campo magnetico, oltre a ruotare in un cerchio, ha anche vibrazioni radiali-Landau livelli (anche nel caso di momento orbitale zero).
In questi 90 anni, soprattutto in esperimenti di risonanza di ciclotrone molto accurati, nessuno ha rilevato le vibrazioni radiali degli elettroni e i livelli di Landau.
Risolvendo questa equazione, Schrödinger, come Sommerfeld, ottenne la formula (5), che descriveva non esattamente la struttura dello spettro dell’idrogeno. Inoltre, dalla soluzione del problema per una particella in un pozzo di potenziale, risulta che una particella con una lunghezza d’onda ƛ=ℏ/mchas stati legati (è posta) in un pozzo di dimensioni arbitrarie e, in particolare, molto più piccolo di ƛ/2. Questo fatto contraddice il principio fondamentale della teoria quantistica (delle onde), il principio di incertezza.
Nel 1925 Schrödinger inviò questo lavoro agli editori di ‘Annalen der Physik’ , ma poi prese il manoscritto, rifiutò gli approcci relativistici e nel 1926 costruì un’equazione d’onda basata sull’espressione hamiltoniana classica, l’equazione di Schrödinger .
L’equazione descriveva lo spettro dell’atomo di idrogeno solo qualitativamente, tuttavia non aveva restrizioni irragionevoli o soluzioni singolari nella forma della formula di Sommerfeld-Dirac. Klein, Fock e Gordon pubblicarono l’equazione relativistica basata sull’equazione d’onda per una particella senza spin nel 1926; è chiamata equazione di Klein-Fock-Gordon.
Con la scoperta dello spin, la situazione cambiò drasticamente, e nel 1926 Heisenberg e Jordan dimostrarono che, nella descrizione di Pauli dello spin di un elettrone, metà dell’energia dell’interazione spin-orbita è uguale a un termine con una potenza di α4 nell’espansione in serie di Taylor della formula di Sommerfeld.
Perché proprio la metà, Thomas ha cercato di spiegarlo nel 1927 con la presenza di una precessione relativistica di un elettrone nel quadro di riferimento del moto lungo l’orbita. L’energia della precessione di Thomas è esattamente uguale alla metà del valore dell’energia dell’interazione spin-orbita con il segno inverso (positivo), che dovrebbe essere aggiunto all’energia dell’interazione spin-orbita. Tuttavia, l’assunzione errata che la frequenza di precessione di Thomas sia identica in entrambi i quadri di riferimento e l’assenza di una derivazione comune e corretta per i quadri di riferimento non inerziali (rotanti) hanno sollevato dubbi sulla correttezza di tali approcci. La ragione della comparsa di metà dell’energia dell’interazione spin-orbita nella formula di Sommerfeld è ancora oggetto di studio ed è uno dei problemi irrisolti della fisica moderna.
D’altra parte, sia nella derivazione della formula di Sommerfeld che nella soluzione dell’equazione di Klein-Fock-Gordon per il problema dell’atomo di idrogeno, inizialmente non si è tenuto conto né dell’energia dello spin né dell’interazione spin-orbita. Pertanto, il fine splitting ottenuto non può in alcun modo essere dovuto all’interazione spin-orbita. Si tratta di un effetto relativistico ma puramente meccanico, quando la massa (inerzia) di una particella dipende già dalla velocità di movimento lungo l’orbita (del momento angolare), per cui il moto radiale dell’elettrone cambia, e viceversa. Proprio questa dipendenza, che porta alla scissione dei livelli energetici dell’elettrone, e all’impossibilità di introdurne uno solo, il numero quantico principale. Tuttavia, anche con questo presupposto, l’ordine di scissione dei livelli secondo la formula (8) contraddice la logica; risulta che maggiore è il momento angolare orbitale, minore è l’energia del livello scisso.
La rappresentazione matriciale dell’onda del secondo ordine Eq. (9) da un sistema di equazioni del primo ordine è la costruzione Dirac dell’equazione relativistica dell’elettrone (le matrici Dirac sono la rappresentazione particolare dei numeri di Clifford-Lipschitz). Nella rappresentazione standard l’equazione di Dirac per una particella libera ha la forma .
dove
sono le matrici di Pauli (la matrice unità nelle formule è omessa).
Per una particella in un campo esterno, l’Eq. (16) è solitamente scritta nella forma
dove per una rappresentazione invariante nel caso di una particella libera, le equazioni sono composte per la differenza tra la quantità di moto generalizzata e la quantità di moto del campo.
Nel caso dell’energia potenziale di una carica immobile in un campo di Coulomb, si ottiene la formula di Sommerfeld-Dirac come risultato di una soluzione esatta di questa particolare equazione. Lì, di nuovo, anche se per un sistema con spin 1/2l’energia dell’interazione spin-orbita non è presa in considerazione inizialmente, ma la metà è ottenuta dalla soluzione esatta del problema dell’atomo di idrogeno.
Misure più accurate di Lamb nel 1947 e successivi miglioramenti nello spettro dell’atomo di idrogeno hanno rivelato che, oltre alle linee con il massimo j, anche tutte le altre sono divise e un po’ spostate (lo spostamento di Lamb). Per armonizzare i risultati della teoria con dati sperimentali più precisi sullo spettro dell’atomo di idrogeno, si dovevano proporre altre soluzioni e approcci rispetto a quelli stabiliti dalla derivazione dell’equazione di Dirac.
I nuovi approcci teorici non avevano fruttato nulla e avevano solo integrato la teoria con delle proposte illogiche e non fisiche per superare la singolarità emergente delle soluzioni: la rinormalizzazione, la differenza finita di infiniti con il valore desiderato della differenza, e così via. La contabilizzazione della dimensione del nucleo ha corretto solo il valore Z in un valore maggiore, ma non ha risolto il problema Z>137. Un risultato incredibile è stato ottenuto anche per il problema dell’atomo di idrogeno che l’elettrone si trova, molto probabilmente, al centro dell’atomo, cioè nel nucleo.
I risultati della soluzione del problema per una particella in un pozzo di potenziale sia nel caso dell’equazione di Klein-Fock-Gordon che dell’equazione di Dirac contraddicono al principio fondamentale della meccanica quantistica, al principio di indeterminazione. Dalle soluzioni risulta che una particella può trovarsi in uno stato vincolato in un pozzo di qualsiasi dimensione, in particolare con dimensioni molto più piccole della lunghezza d’onda della particella stessa, A=ℏ/mc.
Nonostante Dirac stesso abbia proposto un sistema di equazioni relativistiche lineari di primo grado nella rappresentazione matriciale che descriveva il sistema con spin 1/2, le contraddizioni non scomparvero, ed egli stesso rimase insoddisfatto dei risultati della sua teoria. Come scrisse Dirac nel 1956, lo sviluppo della teoria relativistica degli elettroni può ora essere considerato come un esempio di come argomenti errati portino talvolta a un risultato valido. Negli anni ’70, divenne chiaro che la teoria relativistica della meccanica quantistica non esiste, e che bisognava cercare nuovi approcci ed equazioni fondamentali per costruire una teoria coerente della meccanica quantistica relativistica. E negli anni ’80, Dirac parlava già delle difficoltà insuperabili della teoria quantistica esistente e della necessità di crearne una nuova.
La ragione del fallimento di queste teorie è abbastanza semplice: è nell’ignorare la dipendenza dell’energia di interazione con il campo dalla velocità della particella. La quantità di moto generalizzata del sistema, la particella più il campo esterno, è la somma dell’espressione relativistica per la quantità di moto meccanica della particella e la quantità di moto del campo nel caso di interazione con la particella immobile
che non è una rappresentazione invariante della velocità della particella. Per costruire qualche invariante da tale rappresentazione, è stata usata in tutti i casi una relazione ‘invariante’ sotto forma di differenza tra il momento generalizzato del sistema e il momento del campo nel caso di interazione con la particella immobile
Ovviamente, la permutazione delle componenti del momento generalizzato per la costruzione dell’invariante non risolve il problema posto. L’affermazione che l’espressione (20) è la quantità di moto meccanica di una particella e quindi è un invariante non è dimostrata ed è necessario apprendere la formula (20) come empirica. Pertanto, ad alte velocità o forti interazioni, si verifica una dipendenza non calcolata dell’energia di interazione della particella con il campo dalla velocità del moto della particella, che porta a risultati errati o all’impossibilità di calcoli.
In , è stata proposta una rappresentazione invariante della quantità di moto generalizzata del sistema, dove la dipendenza dell’energia di interazione della particella con il campo sulla velocità è stata presa in considerazione:
che è la rappresentazione quadridimensionale della quantità di moto generalizzata del sistema basata sull’espressione per la quantità di moto generalizzata di una particella immobile in stato di riposo
il cui invariante è sempre uguale all’espressione (19) indipendentemente dallo stato del sistema.
L’applicazione dei principi variazionali per costruire la teoria relativistica e quantistica si è basata sui principi di costruzione della meccanica con l’aiuto della lagrangiana del sistema, che originariamente non era destinata agli approcci relativistici. La costruzione lagrangiana è parametrica con una variabile temporale τ = ct, individuata tra le variabili dello spazio quadridimensionale (il resto è rappresentato dalla dipendenza da questa variabile τ) e contiene il differenziale totale rispetto a questa variabile, la velocità della particella. Tale costruzione è inaccettabile a causa dell’impossibilità di applicare il principio di invarianza della rappresentazione delle variabili e la rappresentazione covariante dell’azione del sistema.
In , per costruire la teoria relativistica sulla base dei principi variazionali, sono state considerate le soluzioni canoniche (non parametriche) del problema variazionale per funzioni integrali canonicamente definite e sono state scritte le soluzioni canoniche dei problemi variazionali della meccanica negli spazi di Minkowski. Grazie all’unificazione dei principi variazionali di minima azione, flusso e iperflusso, si ottengono le equazioni canonicamente invarianti per il momento generalizzato. Da queste equazioni, le espressioni per la funzione d’azione e la funzione d’onda sono ottenute come soluzione generale del problema variazionale unificato della meccanica.
Di seguito, presentiamo il principio di invarianza generalizzato e la corrispondente rappresentazione del momento generalizzato del sistema, le equazioni della meccanica relativistica e quantistica, diamo le soluzioni dei problemi del moto della carica in un campo elettrico costante, i problemi per una particella in un pozzo di potenziale e il passaggio di una particella attraverso una barriera di potenziale, i problemi del moto in un campo esponenziale (Morse), i problemi della particella carica in un campo magnetico, e anche i problemi di un atomo di idrogeno sono dati.




