Relativistisen mekaniikan ja kvanttimekaniikan yhtälöt (ilman spiniä)
Esittely
– Epäillä kaikkea tai uskoa kaikkeen on kaksi yhtä kätevää ratkaisua;
kumpikin poistaa pohdinnan välttämättömyyden.
Henri Poincaré (1854-1912)
Tiedän, tiedän, tiedän,
> mutta entä jos oletan – oletanpa! – ympyrän puhtaus on sokaissut meidät näkemästä mitään sen ulkopuolella!
Minun on aloitettava alusta uusin silmin, minun on ajateltava kaikki uudelleen!
Hypathia (∼360-415 jKr.)
Bohr rakensi vuonna 1913 Balmerin empiiristen kaavojen pohjalta atomin mallin, joka perustui orbitaalien liikemäärän kvantisointiin , jota täydennettiin sittemmin yleisemmillä Sommerfeldin kvanttisointisäännöillä. Noina vuosina ei luonnollisesti oletettu spinin tai hiukkasen luontaisen magneettisen momentin olemassaoloa tai varsinkaan spin-orbit-vuorovaikutusta tai vuorovaikutusta ydinspinin kanssa.
Vuonna 1916 Sommerfeld johti relativististen lähestymistapojen puitteissa kaavan vedyn kaltaisen atomin energiatasoille ottamatta huomioon spiniä . Sommerfeld lähti liikkeelle Bohrin atomin mallista ja käytti relativistista suhdetta massan m omaavan vapaan hiukkasen impulssin pand energian E välillä.
jossa con valonnopeus.
Ulkoisessa kentässä, jossa on neliulotteinen potentiaali (φ,A), oletettiin, että hiukkaselle, jolla on varaus q, voidaan käyttää myös tätä suhdetta, jos hiukkasen yleistetyn impulssin lausekkeesta vähennetään kentän neliulotteisen impulssin komponentit (qφ,qA):
Tapauksessa, jossa Coulombin potentiaali φ=Ze/r, jossa e on elektronin varaus, ris etäisyys ytimestä ja Zon atomiluku, saadaan pallokoordinaatistossa
jossa Lis kulmamomentti. Bohr-Sommerfeldin kvantittumisehdot ovat muotoa
joissa nφja nrovat vastaavasti orbitaalinen ja radiaalinen kvanttiluku. Energiatasoille Sommerfeld sai kaavan
jossa pääkvanttiluku n=nr+l+1=1,2,3,…, l=0,1,2,3,…,n-1 ja α=1/137,036on hienorakennevakio. Vuonna 1916 julkaistussa artikkelissa Sommerfeld ”teki kuitenkin onnekkaan virheen” ja johdettu kaava esitettiin seuraavassa muodossa
Kaava (6) kuvasi täydellisesti kaikki vedyn ja muiden samankaltaisten atomien spektrin rakenteen erityispiirteet noiden vuosien mittaustarkkuuden rajoilla, eikä kaavan oikeellisuudesta itsessään ollut mitään epäilyksiä. Siksi Sommerfeldin kaavaa pidettiin empiirisenä, ja kvanttiluvun l sijasta käytettiin ”salaperäistä” sisäistä kvanttilukua, jolla oli puolen kokonaisluvun arvot j=1/2,3/2,5/2,….,n+1/2,otettiin käyttöön, ja kaavaa (6) käytettiin esityksessä
jossa n=nr+j+1/2=1,2,3,…,j=1/2,3/2,5/2,…,n+1/2, ja l:llä on arvot l=0j=1/2:ssä j=1/2:ssä ja l=j±1/2:ssä muissa. Tämä kaava on yhteneväinen vuonna 1928 saadun relativististen Diracin yhtälöiden täsmällisen ratkaisun tuloksen kanssa hiukkaselle, jonka spin on 1/2, ja klassisen lausekkeen kanssa, joka kuvaa liikkumattoman varauksen potentiaalienergiaa Coulombin kentässä ytimessä, jonka järjestysluku on Zin, muodossa Ur=Ze2/r.
Kaava (7) osoitti myös oudon rajan arvolle, jonka varauksen arvolla ytimessä, jonka järjestysluku on Z<137, on, ja jonka ylittävältä osalta kaava menettää merkityksensä. Oli myös ilmeistä, että hahmoteltujen lähestymistapojen, vahvan ja gravitaatiovuorovaikutuksen, puitteissa ei kuvata planeettojen liikkeitä. Ongelma Z<137tai α>1on edelleen relativistisen kvanttimekaniikan ratkaisematon ongelma. Laajentamalla kaava (7) Taylorin sarjan Zα2 suuruusluokan potensseilla Taylorin sarjassa, laajennustarkkuudella potensseilla Zα6 oleviin termeihin asti, saadaan
Schrödinger työskenteli vuosina 1925-1926 hiukkasen aaltofunktiota kuvaavan yhtälön derivoimisen parissa kuvaamalla De Broglie-aaltoja . Yhtälön johtaminen perustui myös relativistiseen suhteeseen (1) hiukkasen impulssin pand energian E välillä, jonka hän esitti energian ja impulssin neliöoperaattoreiden avulla aaltofunktion yhtälön muodossa
Like Sommerfeld, Schrödinger käytti seuraavaa esitystä hiukkaselle ulkoisessa kentässä
Tapauksessa, jossa stationaariset tilat ovat varattu hiukkanen vetyatomin Coulombin potentiaalin kentässä oli ratkaistava yhtälö
Kuten voidaan nähdä, potentiaalienergian q2φ2r/2mc2 kvadraattinen lauseke esiintyy yhtälössä positiivisen merkin kanssa ja vetovoimakenttien tapauksessa ratkaisut johtavat tiettyihin vaikeuksiin. Lähestyttäessä singulariteettipistettä vetovoimat kasvavat negatiivisen merkin vuoksi, ja singulariteetin läsnäolo johtaa tunnettuihin rajoituksiin vuorovaikutusten suuruudelle (kuva 1).
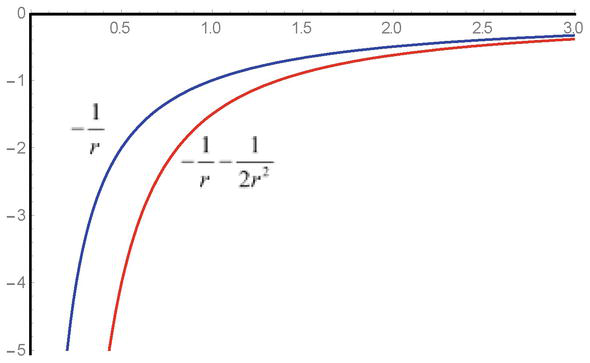
Kuva 1.
Vetovoimakentän potentiaalin-1/ja potentiaalisen vuorovaikutusenergian-1/r-1/2r2 otosriippuvuus Klein-Gordonin yhtälöissä.
Jatkossa aaltovektori kis esitetään
ja tarkasteltaessa ongelmaa, joka koskee energian Eth omaavan hiukkasen kulkua potentiaaliesteen U=qφr läpi(kuva 2), jonka korkeus on suurempi kuin hiukkasen kaksinkertainen lepoenergia U>2mc2, läpäisykerroin muuttuu yhdeksi esteen korkeudesta riippumatta (Kleinin paradoksi) .
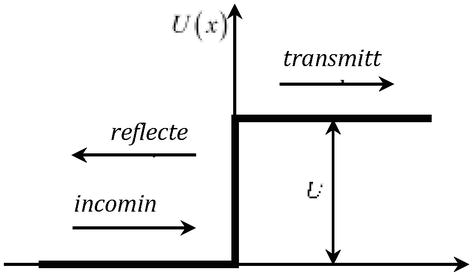
Kuva 2.
Hiukkasen kulku potentiaaliesteen läpiU.
Toinen vaikeus on se, että kuten hiukkasongelman ratkaisu potentiaalikaivossa osoittaa, riittävällä syvyydellä hiukkasella, jonka aallonpituus on ƛ=ℏ/mcc, voi olla sidostiloja (voi lokalisoitua) kaivon leveydellä, joka on kapeampi kuin hiukkasen aallonpituus d<ƛ/2(kuva 3), mikä on ristiriidassa kvanttimekaniikan perustavanlaatuisen periaatteen kanssa-Heisenbergin epätarkkuusperiaatteen kanssa.
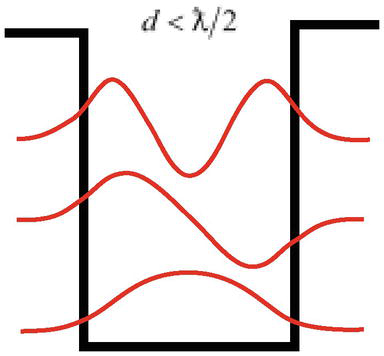
Kuva 3.
Hiukkanen, jonka aallonpituusƛvoi lokalisoitua kuoppaan leveydeltäd<ƛ/2.
Vetyä muistuttavan atomin ongelman ratkaisua rajoittaa myös atomiytimen järjestysluvun arvo Z≤68(Diracin yhtälössä rajoituksena on Z≤137). Sama relativistisessa mekaniikassa – kun tarkastellaan vahvoja vuorovaikutuksia, Hamilton-Jacobyn relativistisen yhtälön ratkaisu osoittaa niin sanotun ”hiukkasen putoamisen keskipisteeseen” .
Voidakseen päästä eroon kvadraattisesta termistä tai kääntää sen merkin päinvastaiseksi on viime vuosina ehdotettu, että potentiaalienergia esitettäisiin Klein-Gordonin ja Diracin yhtälöissä skalaaripotentiaalin ja vektoripotentiaalin lausekkeiden neliöiden erotuksena (S-taajuusyhtälö) . Tällainen matemaattinen formalismi korjaa tilanteen, mutta fysikaalisesta näkökulmasta tällaiset esitykset eivät ole mitenkään perusteltuja, eikä tällaisia pseudopotentiaaleja vastaavia kenttiä ole luonnossa olemassa.
Se on vielä huonompi vektorikentän kvadraattisen termin läsnäollessa, jonka merkin takia saadaan luonnossa olemattomia tiloja ja kokemuksen kanssa ristiriitaisia ratkaisuja.
Kvanttimekaniikan ja Hamilton-Jacobyn yhtälöiden ratkaisujen mukaan, käy ilmi, että magneettikentässä olevalla varautuneella hiukkasella on ympyrän pyörimisen lisäksi myös säteittäisiä värähtelyjä-Landau-tasoja (jopa siinä tapauksessa, että kiertomomentti on nolla).
Näiden 90 vuoden aikana, erityisesti erittäin tarkoissa syklotroniresonanssikokeissa, kukaan ei ole havainnut elektronien säteisvärähtelyjä ja Landaun tasoja.
Tämän yhtälön ratkaisemalla Schrödinger sai Sommerfeldin tavoin kaavan (5), joka ei kuvannut vedyn spektrin rakennetta tarkasti. Lisäksi potentiaalikaivossa olevan hiukkasen ongelman ratkaisusta käy ilmi, että hiukkanen, jonka aallonpituus ƛ=ℏ/mchas sidotut tilat (sijoittuu) mielivaltaisen kokoiseen kaivoon ja erityisesti paljon pienempään kuin ƛ/2. Tämä tosiasia on ristiriidassa kvanttiteorian (aaltoteorian) perusperiaatteen, epävarmuusperiaatteen, kanssa.
Vuonna 1925 Schrödinger lähetti tämän työn ”Annalen der Physik” -lehden toimittajille , mutta otti sitten käsikirjoituksen, kieltäytyi relativistisista lähestymistavoista ja rakensi vuonna 1926 aaltoyhtälön, joka perustuu klassiseen Hamiltonin lausekkeeseen, Schrödingerin yhtälöön .
Yhtälö kuvasi vetyatomin spektriä vain kvalitatiivisesti, mutta sillä ei kuitenkaan ollut kohtuuttomia rajoituksia tai singulaarisia ratkaisuja Sommerfeld-Diracin kaavan muodossa. Klein , Fock ja Gordon julkaisivat vuonna 1926 aaltoyhtälöön perustuvan relativistisen yhtälön hiukkaselle, jolla ei ole spiniä; sitä kutsutaan Klein-Fock-Gordonin yhtälöksi.
Spinin löytymisen myötä tilanne muuttui radikaalisti, ja vuonna 1926 Heisenberg ja Jordan osoittivat, että elektronin spinin Pauli-kuvauksessa puolet spin-orbit-vuorovaikutussuhteen energiasta on yhtä suuri kuin Sommerfeldin kaavan Taylorin sarjan ekspansiossa Sommerfeldin kaavan yhtälön referenssi viitteenä menee tänne.
Miksi juuri puolet, Thomas yritti vuonna 1927 selittää tätä elektronin relativistisella prekessiolla radan suuntaisen liikkeen viitekehyksessä . Thomasin prekession energia on täsmälleen puolet spin-orbit-vuorovaikutuksen energian arvosta käänteisellä (positiivisella) merkillä, joka pitäisi lisätä spin-orbit-vuorovaikutuksen energiaan. Virheellinen oletus, jonka mukaan Thomasin prekessiotaajuus on sama molemmissa viitekehyksissä, ja yhteisen ja oikean johtolaskelman puuttuminen ei-inertialisille (pyöriville) viitekehyksille herättivät kuitenkin epäilyjä tällaisten lähestymistapojen oikeellisuudesta. Syytä spin-orbit-vuorovaikutuksen puolen energian esiintymiseen Sommerfeldin kaavassa tutkitaan edelleen, ja se on yksi nykyfysiikan ratkaisemattomista ongelmista.
Toisaalta sekä Sommerfeldin kaavan johtamisessa että vetyatomiongelman Klein-Fock-Gordonin yhtälön ratkaisussa ei alunperin otettu huomioon spinin eikä spin-orbit-vuorovaikutuksen energiaa. Näin ollen saatu hienojakautuminen ei voi missään tapauksessa johtua spin-orbit-vuorovaikutuksesta. Kyseessä on relativistinen, mutta puhtaasti mekaaninen vaikutus, kun hiukkasen massa (inertia) riippuu jo rataa pitkin tapahtuvan liikkeen nopeudesta (kulmamomentista), minkä vuoksi elektronin säteittäinen liike muuttuu ja päinvastoin. Juuri tämä riippuvuus, joka johtaa elektronin energiatasojen jakautumiseen ja siihen, että on mahdotonta ottaa käyttöön vain yhtä, pääkvanttilukua. Kuitenkin, jopa tällä oletuksella, kaavan (8) mukainen tasojen jakautumisjärjestys on ristiriidassa logiikan kanssa; käy ilmi, että mitä suurempi on radan kiertomomentti, sitä pienempi on jakautuneen tason energia.
Kakkosjärjestyksen aallon matriisiesitys Eq. (9) ensimmäisen kertaluvun yhtälösysteemillä on relativistisen elektroniyhtälön Dirac-konstruktio (Dirac-matriisit ovat Clifford-Lipschitzin lukujen erityinen esitys ). Vakioesityksessä vapaan hiukkasen Diracin yhtälö on muotoa .
joissa
ovat Pauli-matriisit (yksikkömatriisi on kaavoissa jätetty pois).
Ulkoisessa kentässä olevalle hiukkaselle pätee Yht. (16) kirjoitetaan yleensä muodossa
jossa vapaan hiukkasen tapauksessa invariantin esityksen osalta yhtälöt muodostetaan yleistetyn momentin ja kentän momentin erotukselle.
Tapauksessa, jossa on kyse liikkumattoman varauksen potentiaalienergiasta Coulombin kentässä, saadaan Sommerfeld-Diracin kaava tämän nimenomaisen yhtälön tarkan ratkaisun tuloksena. Sielläkin, vaikkakin systeemille, jolla on spin 1/2, spin-orbit-vuorovaikutuksen energiaa ei aluksi oteta huomioon, vaan puolikas saadaan vetyatomin ongelman tarkasta ratkaisusta.
Lambin tarkemmat mittaukset vuonna 1947 ja myöhemmät parannukset vetyatomin spektrissä paljastivat, että j- maksimiviivojen lisäksi kaikki muutkin viivat ovat halkaistuja ja jonkin verran siirtyneitä (Lamb-siirtymä). Jotta teorian tulokset saataisiin sovitettua yhteen vetyatomin spektriä koskevien tarkempien kokeellisten tietojen kanssa, oli ehdotettava muita ratkaisuja ja lähestymistapoja kuin mitä Diracin yhtälön johtaminen asetti.
Uudet teoreettiset lähestymistavat eivät olleet tuottaneet mitään, ja ne vain täydensivät teoriaa epäloogisilla ja ei-fysikaalisilla ehdotuksilla, joilla pyrittiin voittamaan esiin nouseva ratkaisujen singulariteetti: uudelleennormalisointi (renormalisaatio), äärellisten äärettömyyksien differenssi halutulla differenssin arvolla ja niin edelleen. Ytimen koon huomioon ottaminen korjasi vain Z-arvon suuremmaksi, mutta ei ratkaissut Z>137ongelmaa. Uskomaton tulos saatiin myös vetyatomin ongelmalle, että elektroni sijaitsee todennäköisimmin atomin keskipisteessä eli ytimessä.
Potentiaalikaivossa olevan hiukkasen ongelman ratkaisutulokset sekä Klein-Fock-Gordonin yhtälön että Diracin yhtälön tapauksessa ovat ristiriidassa kvanttimekaniikan perusperiaatteen, epävarmuusperiaatteen kanssa. Ratkaisuista käy ilmi, että hiukkanen voi olla sidotussa tilassa kuopassa, jonka mitat ovat mitä tahansa, erityisesti, jos se on kooltaan paljon pienempi kuin itse hiukkasen aallonpituus A=ℏ/mc.
Huolimatta siitä, että Dirac itse ehdotti lineaaristen ensimmäisen asteen relativististen yhtälöiden järjestelmää matriisiesityksessä, joka kuvasi systeemiä, jonka spin oli 1/2, ristiriidat eivät hävinneet, ja hän itse jäi tyytymättömäksi teoriansa tuloksiin. Kuten Dirac kirjoitti vuonna 1956 , relativistisen elektroniteorian kehitystä voidaan nyt pitää esimerkkinä siitä, miten virheelliset argumentit joskus johtavat arvokkaaseen tulokseen. 70-luvulla kävi selväksi, että relativistista kvanttimekaniikan teoriaa ei ole olemassa, ja olisi etsittävä uusia, perustavanlaatuisia lähestymistapoja ja yhtälöitä, jotta relativistisen kvanttimekaniikan johdonmukainen teoria voitaisiin rakentaa. Ja 80-luvulla Dirac puhui jo olemassa olevan kvanttiteorian ylitsepääsemättömistä vaikeuksista ja tarpeesta luoda uusi teoria .
Syy näiden teorioiden epäonnistumiseen on varsin yksinkertainen – se on siinä, että vuorovaikutusenergian riippuvuus kentän kanssa hiukkasen nopeudesta jätetään huomiotta. Systeemin, hiukkasen ja ulkoisen kentän, yleistetty impulssi on hiukkasen mekaanisen impulssin relativistisen lausekkeen ja kentän impulssin summa vuorovaikutustapauksessa liikkumattoman hiukkasen kanssa
joka ei ole invariantti esitys hiukkasen nopeudelle. Jotta tällaisesta esityksestä voitaisiin konstruoida jokin invariantti, käytettiin kaikissa tapauksissa ”invariantti”-suhdetta systeemin yleistetyn impulssin ja kentän impulssin erotuksen muodossa vuorovaikutustapauksessa liikkumattoman hiukkasen kanssa
Yleistetyn momentin komponenttien permutaatio invariantin konstruoimiseksi ei selvästikään ratkaise esitettyä ongelmaa. Väite, että lauseke (20) on hiukkasen mekaaninen momentti ja siten invariantti, on todistamaton ja on tarpeen käsittää kaava (20) empiirisenä. Näin ollen suurilla nopeuksilla tai voimakkaissa vuorovaikutuksissa hiukkasen ja kentän välisen vuorovaikutuksen energian riippuvuus hiukkasen liikenopeudesta jää huomiotta, mikä johtaa virheellisiin tuloksiin tai laskelmien mahdottomuuteen.
Tässä ehdotettiin systeemin yleistetyn momentin invarianttiesitystä, jossa hiukkasen ja kentän vuorovaikutusenergian riippuvuus nopeudesta otettiin huomioon:
joka on systeemin yleistetyn impulssin neliulotteinen esitys, joka perustuu lausekkeeseen liikkumattoman hiukkasen yleistetylle impulssille lepotilassa
jonka invariantti on aina yhtä suuri kuin lausekkeessa (19) riippumatta systeemin tilasta.
Variaatioperiaatteiden soveltaminen relativistisen ja kvanttiteorian rakentamiseen perustui mekaniikan rakentamisen periaatteisiin systeemin Lagrangen avulla , jota ei alun perin ollut tarkoitettu relativistisiin lähestymistapoihin. Lagrangen konstruktiossa on parametrina yksi aikamuuttuja τ = ct, joka on erotettu neliulotteisen avaruuden muuttujista (muut muuttujat edustavat riippuvuutta tästä muuttujasta τ), ja se sisältää kokonaisdifferentiaalin tämän muuttujan, hiukkasen nopeuden, suhteen. Tällaista konstruktiota ei voida hyväksyä, koska muuttujien esityksen invarianssiperiaatetta ja systeemin toiminnan kovarianttiesitystä ei voida soveltaa.
Relativistisen teorian rakentamiseksi variaatioperiaatteiden pohjalta on tarkasteltu kanonisesti määriteltyjen integraalifunktioiden variaatio-ongelman kanonisia (ei-parametrisia) ratkaisuja ja kirjoitettu mekaniikan variaatio-ongelmien kanoniset ratkaisut Minkowski-avaruuksissa. Pienimmän toiminnan, virtauksen ja hypervirtauksen variaatioperiaatteiden yhdistämisen ansiosta saadaan yleistetyn momentin kanonisesti invariantit yhtälöt. Näistä yhtälöistä saadaan toimintafunktion ja aaltofunktion lausekkeet mekaniikan yhtenäistetyn variaatio-ongelman yleiseksi ratkaisuksi.
Alempana esitämme yleistetyn invarianssiperiaatteen ja systeemin yleistetyn momentin vastaavan esityksen, relativistisen ja kvanttimekaniikan yhtälöt , annamme ratkaisut varauksen liikkeen ongelmiin vakiosähkökentässä, hiukkasen ongelmiin potentiaalikaivossa ja hiukkasen kulkuun potentiaaliesteen läpi, eksponentiaalikentän (Morse) liikkeen ongelmiin, varattujen hiukkasten ongelmiin magneettikentässä ja lisäksi annetaan vetyatomin ongelmat.




