Equations de la mécanique relativiste et quantique (sans spin)
Introduction
-Douter de tout ou croire à tout sont deux solutions également commodes;
les unes et les autres dispensent de la nécessité de la réflexion.
Henri Poincaré (1854-1912)
Je sais, je sais, mais supposons – supposons seulement ! – que la pureté du cercle nous ait aveuglés et empêchés de voir quoi que ce soit au-delà !
Je dois tout recommencer avec des yeux neufs, je dois tout repenser !
Hypathie (∼360-415 AD)
En 1913, Bohr, sur la base des formules empiriques de Balmer, construit un modèle d’atome fondé sur la quantification du moment orbital , qui sera ensuite complété par les règles de quantification plus générales de Sommerfeld. Dans ces années, naturellement, la présence d’un spin ou d’un moment magnétique intrinsèque de la particule ou, surtout, l’interaction spin-orbite, ou l’interaction avec le spin nucléaire, n’était pas supposée.
En 1916, Sommerfeld, dans le cadre des approches relativistes, a dérivé une formule pour les niveaux d’énergie d’un atome de type hydrogène, sans tenir compte du spin . Sommerfeld procéda à partir du modèle de l’atome de Bohr et utilisa la relation relativiste entre la quantité de mouvement pand l’énergie Ed’une particule libre de masse m.
où cest la vitesse de la lumière.
Dans un champ externe avec un potentiel quadridimensionnel (φ,A), on a supposé que pour une particule avec la charge qcette relation peut aussi être utilisée si on soustrait les composantes du moment quadridimensionnel du champ (qφ,qA) de l’expression pour le momentum généralisé de la particule:
Dans le cas du potentiel de Coulomb φ=Ze/r, où e est la charge de l’électron, ris la distance au noyau, et Zest un numéro atomique, on obtient en coordonnées sphériques
où Lis le moment cinétique. Les conditions de quantification de Bohr-Sommerfeld prennent la forme
où nφet nra sont les nombres quantiques orbitaux et radiaux, respectivement. Pour les niveaux d’énergie, Sommerfeld a obtenu la formule
où le nombre quantique principal n=nr+l+1=1,2,3,…, l=0,1,2,3,…,n-1, et α=1/137,036est la constante de structure fine. Cependant, dans un article publié en 1916 , Sommerfeld « a fait une erreur heureuse » et la formule dérivée a été présentée sous la forme suivante
La formule (6) décrivait parfaitement toutes les particularités de la structure du spectre de l’hydrogène et d’autres atomes similaires avec la précision limite pour ces années-là des mesures, et il n’y avait aucun doute sur l’exactitude de la formule elle-même. Par conséquent, la formule de Sommerfeld a été perçue comme empirique, et au lieu du nombre quantique l, un nombre quantique interne « mystérieux » avec des valeurs demi-entières j=1/2,3/2,5/2,….,n+1/2a été introduit, et la formule (6) a été utilisée dans la représentation
où n=nr+j+1/2=1,2,3,…,j=1/2,3/2,5/2,…,n+1/2, et l possèdent les valeurs l=0à j=1/2et l=j±1/2pour les autres. Cette formule coïncide avec le résultat d’une solution exacte des équations relativistes de Dirac en 1928 pour une particule de spin 1/2avec l’expression classique de l’énergie potentielle d’une charge immobile dans le champ de Coulomb d’un noyau de numéro atomique Zsous la forme Ur=Ze2/r.
La formule (7) indiquait aussi une étrange limitation de valeur la charge d’un noyau de numéro atomique Z<137, au-delà de laquelle la formule perd son sens. Il était également évident que dans le cadre des approches exposées, les interactions fortes et gravitationnelles, les mouvements des planètes ne sont pas décrits. Le problème Z<137ou α>1reste le problème non résolu de la mécanique quantique relativiste. En développant la formule (7) sur l’ordre des puissances Zα2 dans la série de Taylor, avec une précision de développement jusqu’aux termes par les puissances Zα6, on obtient
En 1925-1926, Schrödinger a travaillé sur la dérivation de l’équation de la fonction d’onde d’une particule décrivant les ondes de De Broglie . La dérivation de l’équation était également basée sur la relation relativiste (1) entre la quantité de mouvement et l’énergie Ede la particule, qu’il présenta à l’aide des opérateurs des carrés de l’énergie et du momentum sous la forme d’une équation pour la fonction d’onde
Comme Sommerfeld, Schrödinger utilisait la représentation suivante pour une particule dans un champ extérieur
Dans le cas d’états stationnaires d’une particule chargée dans le champ du potentiel de Coulomb pour un atome d’hydrogène, il était nécessaire de résoudre l’équation
Comme on peut le voir, l’expression quadratique de l’énergie potentielle q2φ2r/2mc2est présente dans l’équation avec un signe positif et dans le cas de champs attractifs, les solutions conduisent à certaines difficultés. À l’approche du point de singularité, en raison du signe négatif, les forces d’attraction augmentent et la présence de la singularité conduit à des limitations connues de l’ampleur des interactions (figure 1).
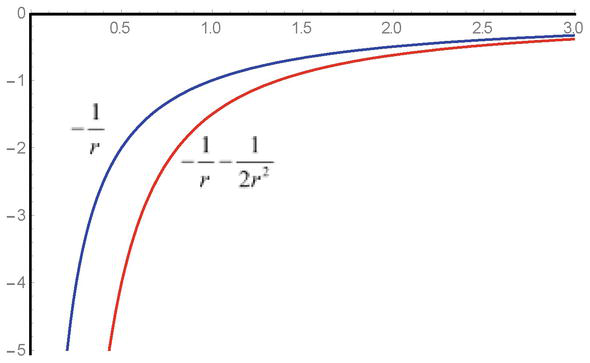
Figure 1.
Dépendance de l’échantillon du potentiel du champ attractif-1/et de l’énergie d’interaction potentielle-1/r-1/2r2dans les équations de Klein-Gordon.
Puis, le vecteur d’onde k est représenté comme
et lorsqu’on considère le problème du passage d’une particule d’énergie Eth à travers une barrière de potentiel U=qφr(Figure 2), dont la hauteur est supérieure à l’énergie de repos doublée de la particule U>2mc2, le coefficient de transmission devient unitaire, quelle que soit la hauteur de la barrière (paradoxe de Klein) .
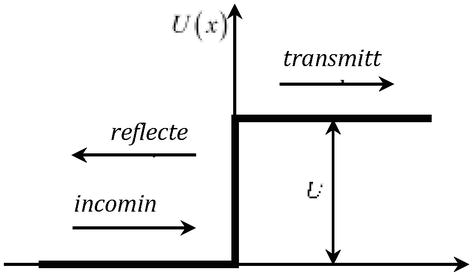
Figure 2.
Passage d’une particule à travers une barrière potentielleU.
Une autre difficulté est que, comme le montre la solution du problème des particules dans un puits de potentiel, à une profondeur suffisante, une particule de longueur d’onde ƛ=ℏ/mcc peut avoir des états liés (peut être localisée) dans une largeur de puits plus étroite que la longueur d’onde de la particule d<ƛ/2(Figure 3), ce qui contredit le principe fondamental de la mécanique quantique, le principe d’incertitude d’Heisenberg.
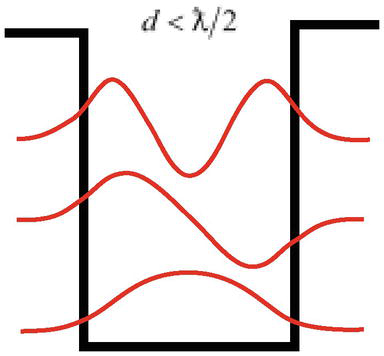
Figure 3.
Une particule de longueur d’ondeƛpeut être localisée dans un puits de largeurd<ƛ/2.
Aussi, la solution du problème d’un atome de type hydrogène est limitée par la valeur du numéro ordinal du noyau atomique Z≤68(pour l’équation de Dirac, la restriction du numéro atomique est Z≤137). La même chose en mécanique relativiste – lorsque l’on considère les interactions fortes, la solution de l’équation relativiste de Hamilton-Jacoby indique la soi-disant « chute de la particule sur le centre » .
Afin de se débarrasser du terme quadratique ou d’inverser son signe, ces dernières années, il a été proposé de représenter l’énergie potentielle dans les équations de Klein-Gordon et de Dirac comme la différence des carrés des expressions des potentiels scalaires et vectoriels (équation des ondes S) . Un tel formalisme mathématique corrige la situation, mais d’un point de vue physique de telles représentations ne sont nullement justifiées, et les champs correspondant à de tels pseudo-potentiels n’existent pas dans la nature.
Les choses sont encore pires avec la présence d’un terme quadratique du champ vectoriel, à cause du signe duquel on obtient des états inexistants dans la nature et des solutions qui contredisent l’expérience.
Selon les solutions des équations de la mécanique quantique et de Hamilton-Jacoby, il s’avère qu’une particule chargée dans un champ magnétique, en plus de tourner sur un cercle, possède également des vibrations radiales – niveaux de Landau (même dans le cas d’un moment orbital nul).
Au cours de ces 90 années, notamment dans des expériences très précises de résonance cyclotronique, aucun n’a détecté les vibrations radiales des électrons et les niveaux de Landau.
En résolvant cette équation, Schrödinger, comme Sommerfeld, a obtenu la formule (5), qui décrivait la structure du spectre de l’hydrogène de manière non exacte. De plus, à partir de la solution du problème pour une particule dans un puits de potentiel, il s’avère qu’une particule avec une longueur d’onde ƛ=ℏ/mchas bound states (est placée) dans un puits de taille arbitraire et, en particulier, beaucoup plus petite que ƛ/2. Ce fait contredit le principe fondamental de la théorie (des ondes) quantique, le principe d’incertitude.
En 1925, Schrödinger envoie ce travail aux éditeurs des ‘Annalen der Physik’ , mais il reprend ensuite le manuscrit, refuse les approches relativistes et construit en 1926 une équation d’onde basée sur l’expression hamiltonienne classique, l’équation de Schrödinger .
L’équation ne décrivait le spectre de l’atome d’hydrogène que qualitativement, cependant, elle ne présentait pas de restrictions déraisonnables ni de solutions singulières sous la forme de la formule de Sommerfeld-Dirac. Klein , Fock et Gordon ont publié l’équation relativiste basée sur l’équation d’onde pour une particule sans spin en 1926 ; elle est appelée l’équation de Klein-Fock-Gordon.
Avec la découverte du spin, la situation a changé radicalement, et en 1926 Heisenberg et Jordan ont montré que, dans le cadre de la description de Pauli du spin d’un électron, la moitié de l’énergie de l’interaction spin-orbite est égale à un terme avec une puissance de α4 dans l’expansion de la série de Taylor de la référence de l’équation de la formule de Sommerfeld va ici.
Pourquoi exactement la moitié, Thomas a essayé d’expliquer cela en 1927 par la présence d’une précession relativiste d’un électron dans le cadre de référence du mouvement le long de l’orbite . L’énergie de la précession de Thomas est exactement égale à la moitié de la valeur de l’énergie de l’interaction spin-orbite avec le signe inverse (positif), qui devrait être ajoutée à l’énergie de l’interaction spin-orbite. Toutefois, l’hypothèse incorrecte selon laquelle la fréquence de précession de Thomas est identique dans les deux cadres de référence et l’absence d’une dérivation commune et correcte pour les cadres de référence non inertiels (en rotation) ont fait naître des doutes quant à l’exactitude de ces approches. La raison de l’apparition de la moitié de l’énergie de l’interaction spin-orbite dans la formule de Sommerfeld est toujours en cours d’investigation et constitue l’un des problèmes non résolus de la physique moderne.
D’autre part, tant dans la dérivation de la formule de Sommerfeld que lors de la résolution de l’équation de Klein-Fock-Gordon pour le problème de l’atome d’hydrogène , ni le spin ni l’énergie de l’interaction spin-orbite n’ont été pris en compte initialement. Par conséquent, le fractionnement fin obtenu ne peut en aucun cas être dû à l’interaction spin-orbite. Il s’agit d’un effet relativiste mais purement mécanique, lorsque la masse (inertie) d’une particule dépend déjà de la vitesse de déplacement le long de l’orbite (du moment angulaire), à cause de laquelle le mouvement radial de l’électron change, et vice versa. C’est justement cette dépendance qui entraîne le fractionnement des niveaux d’énergie de l’électron et l’impossibilité d’en introduire un seul, le nombre quantique principal. Néanmoins, même avec cette hypothèse, l’ordre de fractionnement des niveaux selon la formule (8) est en contradiction avec la logique ; il s’avère que plus le moment angulaire orbital est grand, plus l’énergie du niveau fractionné est faible.
La représentation matricielle de l’onde de second ordre Eq. (9) par un système d’équations du premier ordre est la construction de Dirac de l’équation relativiste de l’électron (les matrices de Dirac sont la représentation particulière des nombres de Clifford-Lipschitz ). Dans la représentation standard, l’équation de Dirac pour une particule libre a la forme .
où
sont les matrices de Pauli (la matrice unité dans les formules est omise).
Pour une particule dans un champ externe, Eq. (16) s’écrit généralement sous la forme
où pour une représentation invariante dans le cas d’une particule libre, les équations sont composées pour la différence entre le momentum généralisé et le momentum du champ.
Dans le cas de l’énergie potentielle d’une charge immobile dans un champ de Coulomb, on obtient la formule de Sommerfeld-Dirac comme résultat d’une solution exacte de cette équation particulière. Là encore, bien que pour un système de spin 1/2l’énergie de l’interaction spin-orbite n’est pas prise en compte initialement, mais la moitié est obtenue à partir de la solution exacte du problème de l’atome d’hydrogène.
Des mesures plus précises de Lamb en 1947 et les améliorations ultérieures du spectre de l’atome d’hydrogène ont révélé qu’en plus des raies avec le maximum j, toutes les autres sont également dédoublées et quelque peu déplacées (le décalage de Lamb). Pour harmoniser les résultats de la théorie avec des données expérimentales plus précises sur le spectre de l’atome d’hydrogène, il fallait proposer d’autres solutions et approches que celles prévues par la dérivation de l’équation de Dirac.
Les nouvelles approches théoriques n’avaient rien donné et ne faisaient que compléter la théorie avec les propositions illogiques et non physiques pour surmonter la singularité émergente des solutions : la renormalisation, la différence finie des infinis avec la valeur désirée de la différence, et ainsi de suite. La prise en compte de la taille du noyau n’a corrigé que la valeur Z en une valeur plus grande, mais n’a pas résolu le problème Z>137. Un résultat incroyable a également été obtenu pour le problème de l’atome d’hydrogène selon lequel l’électron est situé, très probablement, au centre de l’atome, c’est-à-dire dans le noyau.
Les résultats de la résolution du problème d’une particule dans un puits de potentiel à la fois dans le cas de l’équation de Klein-Fock-Gordon et de l’équation de Dirac sont en contradiction avec le principe de base de la mécanique quantique, avec le principe d’incertitude. D’après les solutions, il s’avère qu’une particule peut être dans un état lié dans un puits de n’importe quelles dimensions, en particulier, avec la taille beaucoup plus petite que la longueur d’onde de la particule elle-même, A=ℏ/mc.
Malgré le fait que Dirac lui-même ait proposé un système d’équations relativistes linéaires du premier degré dans la représentation matricielle qui décrivait le système de spin 1/2, les contradictions n’ont pas disparu, et il est lui-même resté insatisfait des résultats de sa théorie. Comme l’écrivait Dirac en 1956, le développement de la théorie relativiste des électrons peut maintenant être considéré comme un exemple de la façon dont des arguments incorrects peuvent parfois conduire à un résultat valable. Dans les années 70, il est devenu évident que la théorie relativiste de la mécanique quantique n’existe pas, et qu’il faut chercher de nouvelles approches et équations fondamentales pour construire une théorie cohérente de la mécanique quantique relativiste. Et dans les années 80, Dirac parlait déjà des difficultés insurmontables de la théorie quantique existante et de la nécessité d’en créer une nouvelle .
La raison de l’échec de ces théories est assez simple – elle se trouve dans l’ignorance de la dépendance de l’énergie d’interaction avec le champ sur la vitesse de la particule. Le momentum généralisé du système, la particule plus le champ extérieur, est la somme de l’expression relativiste du momentum mécanique de la particule et du momentum du champ dans le cas de l’interaction avec la particule immobile
qui n’est pas une représentation invariante de la vitesse de la particule. Pour construire un quelconque invariant à partir d’une telle représentation, une relation ‘invariante’ a été utilisée dans tous les cas sous la forme d’une différence entre le momentum généralisé du système et le momentum du champ dans le cas de l’interaction avec la particule immobile
De toute évidence, la permutation des composantes du momentum généralisé pour la construction de l’invariant ne résout pas le problème posé. L’affirmation selon laquelle l’expression (20) est le moment mécanique d’une particule et donc est un invariant n’est pas prouvée et il est nécessaire d’appréhender la formule (20) comme un empirique. Par conséquent, à des vitesses élevées ou à des interactions fortes, une dépendance non prise en compte de l’énergie d’interaction de la particule avec le champ par rapport à la vitesse du mouvement de la particule, ce qui aboutit à des résultats erronés ou à l’impossibilité des calculs.
En , une représentation invariante de la quantité de mouvement généralisée du système a été proposée, où la dépendance de l’énergie d’interaction de la particule avec le champ sur la vitesse a été prise en compte :
qui est la représentation quadridimensionnelle du momentum généralisé du système basée sur l’expression du momentum généré d’une particule immobile dans un état de repos
dont l’invariant est toujours égal à l’expression (19) quel que soit l’état du système.
L’application des principes variationnels pour construire la théorie relativiste et quantique était basée sur les principes de construction la mécanique à l’aide du Lagrangien du système , qui à l’origine n’était pas destiné aux approches relativistes. La construction lagrangienne est paramétrique avec une seule variable temporelle τ = ct, isolée des variables de l’espace à quatre dimensions (les autres sont représentées par la dépendance à cette variable τ) et contient la différentielle totale par rapport à cette variable, la vitesse de la particule. Une telle construction est inacceptable à cause de l’impossibilité d’appliquer le principe d’invariance de la représentation des variables et de la représentation covariante de l’action du système.
Dans , pour construire la théorie relativiste sur la base des principes variationnels, les solutions canoniques (non paramétriques) du problème variationnel pour les fonctionnelles intégrales canoniquement définies ont été considérées et les solutions canoniques des problèmes variationnels de la mécanique dans les espaces de Minkowski sont écrites. En unifiant les principes variationnels de la moindre action, du flux et de l’hyperflux, on obtient les équations canoniquement invariantes de la quantité de mouvement généralisée. A partir de ces équations, les expressions de la fonction d’action et de la fonction d’onde sont obtenues comme solution générale du problème variationnel unifié de la mécanique.
Ci-après, on présente le principe d’invariance généralisée et la représentation correspondante du momentum généralisé du système, les équations de la mécanique relativiste et quantique , on donne les solutions des problèmes du mouvement de la charge dans un champ électrique constant, les problèmes pour une particule dans un puits de potentiel et le passage d’une particule à travers une barrière de potentiel, les problèmes du mouvement dans un champ exponentiel (Morse), les problèmes de la particule chargée dans un champ magnétique, et aussi les problèmes d’un atome d’hydrogène sont donnés.




