Rozwiązania mechaniki relatywistycznej i kwantowej (bez spinu)
Wprowadzenie
-Wątpić we wszystko lub wierzyć we wszystko to dwa równie wygodne rozwiązania;
jedno i drugie uwalnia od konieczności refleksji.
Henri Poincaré (1854-1912)
Wiem, wiem, ale przypuśćmy – tylko przypuśćmy! –
Muszę zacząć wszystko od nowa z nowymi oczami, muszę wszystko przemyśleć!
Hypatia (∼360-415 n.e.)
W 1913 roku Bohr, opierając się na wzorach empirycznych Balmera, skonstruował model atomu oparty na kwantyzacji orbitalnego momentu pędu , który został następnie uzupełniony o bardziej ogólne reguły kwantyzacji Sommerfelda. W tych latach, naturalnie, obecność spinu lub wewnętrznego momentu magnetycznego cząstki lub, w szczególności, oddziaływanie spin-orbita, lub oddziaływanie ze spinem jądrowym, nie było zakładane.
W 1916 roku, Sommerfeld, w ramach relatywistycznych podejść, wyprowadził wzór na poziomy energetyczne atomu wodoru, nie biorąc pod uwagę spinu . Sommerfeld wyszedł od modelu atomu Bohra i wykorzystał relatywistyczną zależność pomiędzy pędem i energią E swobodnej cząstki o masie m.
gdzie c jest prędkością światła.
W zewnętrznym polu o czterowymiarowym potencjale (φ,A) przypuszczano, że dla cząstki o ładunku q można również skorzystać z tej zależności, jeżeli od wyrażenia na uogólniony moment pędu cząstki odejmiemy składowe czterowymiarowego momentu pędu pola (qφ,qA):
W przypadku potencjału Coulomba φ=Ze/r, gdzie e jest ładunkiem elektronu, ris odległością od jądra, a Z jest liczbą atomową, otrzymujemy we współrzędnych sferycznych
gdzie Lis momentem pędu. Warunki kwantowania Bohra-Sommerfelda mają postać
gdzie nφ i nra są odpowiednio orbitalną i radialną liczbą kwantową. Dla poziomów energetycznych Sommerfeld otrzymał wzór
gdzie główna liczba kwantowa n=nr+l+1=1,2,3,…, l=0,1,2,3,…,n-1, a α=1/137.036jest stałą struktury subtelnej. Jednak w pracy opublikowanej w 1916 roku Sommerfeld „popełnił szczęśliwą pomyłkę” i wyprowadzony wzór przedstawił w następującej postaci
Wzór (6) doskonale opisywał wszystkie osobliwości struktury widma wodoru i innych podobnych atomów z graniczną dla tamtych lat dokładnością pomiarów, a co do poprawności samego wzoru nie było żadnych wątpliwości. Dlatego wzór Sommerfelda uznano za empiryczny, a zamiast liczby kwantowej l wprowadzono „tajemniczą” wewnętrzną liczbę kwantową o wartościach półintegralnych j=1/2,3/2,5/2,…., n+1/2 i wzór (6) został użyty w reprezentacji
gdzie n=nr+j+1/2=1,2,3,…,j=1/2,3/2,5/2,…,n+1/2, a l ma wartości l=0 przy j=1/2 i l=j±1/2 dla pozostałych. Wzór ten pokrywa się z wynikiem dokładnego rozwiązania relatywistycznych równań Diraca w 1928 roku dla cząstki o spinie 1/2 z klasycznym wyrażeniem na energię potencjalną nieruchomego ładunku w polu Coulomba jądra o liczbie atomowej Z w postaci Ur=Ze2/r.
Formuła (7) wskazywała też na dziwne ograniczenie wartości ładunku jądra o liczbie atomowej Z<137, powyżej którego wzór traci sens. Widać też było, że w ramach przedstawionych podejść, oddziaływań silnych i grawitacyjnych, ruchy planet nie są opisane. Problem Z<137lub α>1 pozostaje nierozwiązanym problemem relatywistycznej mechaniki kwantowej. Rozszerzając wzór (7) na rząd potęg Zα2 w szereg Taylora, z dokładnością do rozwinięcia do członów przez potęgi Zα6, otrzymujemy
W latach 1925-1926 Schrödinger pracował nad wyprowadzeniem równania funkcji falowej cząstki opisującego fale De Broglie’a . Podstawą wyprowadzenia tego równania była relatywistyczna zależność (1) między pędem a energią E cząstki, którą przedstawił za pomocą operatorów kwadratów energii i pędu w postaci równania dla funkcji falowej
Podobnie jak Sommerfeld, Schrödinger używał następującej reprezentacji dla cząstki w polu zewnętrznym
W przypadku stanów stacjonarnych cząstki naładowanej w polu naładowanej cząstki w polu potencjału Coulomba dla atomu wodoru konieczne było rozwiązanie równania
Jak widać, kwadratowy wyraz energii potencjalnej q2φ2r/2mc2 jest obecny w równaniu ze znakiem dodatnim i w przypadku pól przyciągających rozwiązania prowadzą do pewnych trudności. Przy zbliżaniu się do punktu osobliwości, ze względu na ujemny znak, siły przyciągające rosną, a obecność osobliwości prowadzi do znanych ograniczeń na wielkość oddziaływań (Rysunek 1).
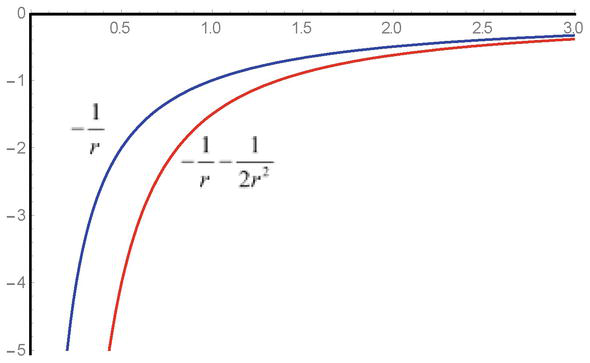
Rysunek 1.
Próbkowa zależność potencjału pola przyciągającego-1/i energii potencjalnej oddziaływania-1/r-1/2r2 w równaniach Kleina-Gordona.
Następnie, wektor falowy k jest reprezentowany jako
i przy rozważaniu problemu przejścia cząstki o energii Eth przez barierę potencjału U=qφr(rysunek 2), której wysokość jest większa od podwojonej energii spoczynkowej cząstki U>2mc2 , współczynnik transmisji staje się równy jedności, niezależnie od wysokości bariery (paradoks Kleina) .
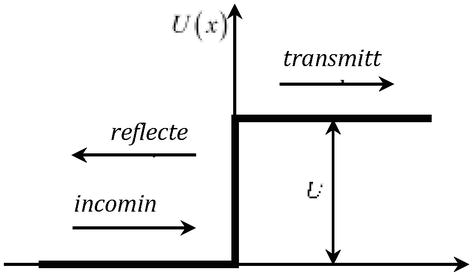
Rysunek 2.
Przejście cząstki przez barierę potencjałuU.
Inna trudność polega na tym, że jak pokazuje rozwiązanie problemu cząstki w studni potencjału, na wystarczającej głębokości cząstka o długości fali ƛ=ℏ/mccan może mieć stany związane (może być zlokalizowana) w studni o szerokości węższej niż długość fali cząstki d<ƛ/2(Rysunek 3), co przeczy podstawowej zasadzie mechaniki kwantowej – zasadzie nieoznaczoności Heisenberga.
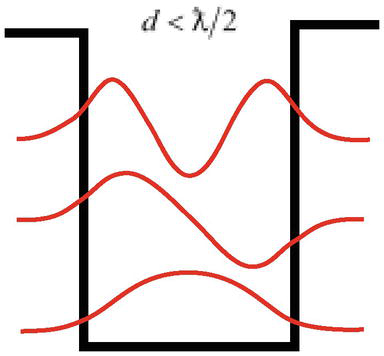
Rysunek 3.
Cząstka o długości faliƛ może być zlokalizowana w studni o szerokościd<ƛ/2.
Również rozwiązanie problemu atomu wodoru jest ograniczone przez wartość liczby porządkowej jądra atomowego Z≤68 (dla równania Diraca ograniczeniem liczby atomowej jest Z≤137). Podobnie w mechanice relatywistycznej – przy rozpatrywaniu oddziaływań silnych, rozwiązanie relatywistycznego równania Hamiltona-Jacoby’ego wskazuje na tzw. „spadek cząstki na centrum” .
Aby pozbyć się członu kwadratowego lub odwrócić jego znak, w ostatnich latach zaproponowano, aby energię potencjalną w równaniach Kleina-Gordona i Diraca przedstawiać jako różnicę kwadratów z wyrażeń potencjałów skalarnych i wektorowych (równanie S-fali) . Taki formalizm matematyczny koryguje sytuację, ale z fizycznego punktu widzenia takie reprezentacje nie są w żaden sposób uzasadnione, a pola odpowiadające takim pseudopotencjałom nie istnieją w przyrodzie.
Jeszcze gorzej jest z obecnością kwadratowego członu pola wektorowego, ze względu na znak którego otrzymujemy nieistniejące w przyrodzie stany i rozwiązania sprzeczne z doświadczeniem.
Zgodnie z rozwiązaniami równań mechaniki kwantowej i Hamiltona-Jacoby’ego, okazuje się, że cząstka naładowana w polu magnetycznym, oprócz tego, że obraca się po okręgu, posiada również drgania radialne – poziomy Landau (nawet w przypadku zerowego pędu orbitalnego).
Przez te 90 lat, szczególnie w bardzo dokładnych eksperymentach rezonansu cyklotronowego, nikt nie wykrył promienistych drgań elektronów i poziomów Landaua.
Rozwiązując to równanie Schrödinger, podobnie jak Sommerfeld, otrzymał wzór (5), który opisywał strukturę widma wodoru niezbyt dokładnie. Co więcej, z rozwiązania problemu dla cząstki w studni potencjału okazuje się, że cząstka o długości fali ƛ=ℏ/mchas bound states (jest umieszczona) w studni o dowolnych rozmiarach, a w szczególności znacznie mniejszych niż ƛ/2. Fakt ten zaprzecza podstawowej zasadzie teorii kwantowej (falowej), zasadzie nieoznaczoności.
W 1925 roku Schrödinger wysłał tę pracę do redakcji „Annalen der Physik” , ale następnie wziął rękopis, odrzucił podejścia relatywistyczne i w 1926 roku zbudował równanie falowe oparte na klasycznym wyrażeniu hamiltonowskim, równaniu Schrödingera .
Równanie opisywało widmo atomu wodoru jedynie jakościowo, nie posiadało jednak żadnych nieuzasadnionych ograniczeń ani rozwiązań osobliwych w postaci wzoru Sommerfelda-Diraca. Klein , Fock i Gordon opublikowali w 1926 roku relatywistyczne równanie oparte na równaniu falowym dla cząstki bez spinu; nazywane jest ono równaniem Kleina-Focka-Gordona.
Z chwilą odkrycia spinu sytuacja zmieniła się diametralnie i w 1926 roku Heisenberg i Jordan pokazali, że w ramach opisu spinu elektronu według Pauliego połowa energii oddziaływania spin-orbita jest równa członowi o potędze α4 w rozwinięciu szeregu Taylora równania wzoru Sommerfelda.
Dlaczego dokładnie połowa, Thomas próbował wyjaśnić to w 1927 roku przez obecność relatywistycznej precesji elektronu w ramie odniesienia ruchu wzdłuż orbity . Energia precesji Thomasa jest dokładnie równa połowie wartości energii oddziaływania spin-orbita z odwrotnym (dodatnim) znakiem, która powinna być dodana do energii oddziaływania spin-orbita. Jednak błędne założenie, że częstość precesji Thomasa jest identyczna w obu układach odniesienia oraz brak wspólnego i poprawnego wyprowadzenia dla nieinercjalnych (rotujących) układów odniesienia wzbudziły wątpliwości co do poprawności takiego podejścia. Przyczyna pojawienia się połowy energii oddziaływania spin-orbita we wzorze Sommerfelda jest nadal badana i jest jednym z nierozwiązanych problemów współczesnej fizyki.
Z drugiej strony, zarówno w wyprowadzeniu wzoru Sommerfelda jak i przy rozwiązywaniu równania Kleina-Focka-Gordona dla problemu atomu wodoru, ani spin, ani energia oddziaływania spin-orbita nie były początkowo brane pod uwagę. Dlatego też, otrzymany drobny podział nie może być w żaden sposób zawdzięczany oddziaływaniu spin-orbita. Jest to relatywistyczny, ale czysto mechaniczny efekt, kiedy masa (bezwładno¶ć) cz±stki zależy już od prędko¶ci ruchu po orbicie (od momentu pędu), przez co zmienia się ruch radialny elektronu i odwrotnie. Właśnie ta zależność, skutkuje rozszczepieniem poziomów energetycznych elektronu, oraz niemożliwością wprowadzenia tylko jednego, głównej liczby kwantowej. Niemniej jednak, nawet przy takim założeniu, kolejność rozszczepienia poziomów według wzoru (8) jest sprzeczna z logiką; okazuje się, że im większy orbitalny moment pędu, tym mniejsza energia rozszczepionego poziomu.
Odwzorowanie macierzowe fali drugiego rzędu Eq. (9) przez układ równań pierwszego rzędu jest konstrukcją Diraca relatywistycznego równania elektronowego (macierze Diraca są szczególną reprezentacją liczb Clifforda-Lipschitza ). W standardowej reprezentacji równanie Diraca dla cząstki swobodnej ma postać .
gdzie
są macierzami Pauliego (macierz jednostkowa we wzorach jest pominięta).
Dla cząstki znajdującej się w polu zewnętrznym, równanie (16) zapisuje się zwykle w postaci (16) zapisuje się zwykle w postaci
gdzie dla reprezentacji niezmienniczej w przypadku cząstki swobodnej, równania są złożone dla różnicy pomiędzy uogólnionym pędem a pędem pola.
W przypadku energii potencjalnej nieruchomego ładunku w polu Coulomba, otrzymujemy wzór Sommerfelda-Diraca jako wynik dokładnego rozwiązania tego szczególnego równania. Tam znowu, chociaż dla układu ze spinem 1/2 energia oddziaływania spin-orbita nie jest początkowo brana pod uwagę, ale połowa jest otrzymywana z dokładnego rozwiązania problemu atomu wodoru.
Dokładniejsze pomiary Lamba w 1947 roku i późniejsze ulepszenia widma atomu wodoru ujawniły, że oprócz linii z maksymalnym j, wszystkie inne są również rozszczepione i nieco przesunięte (przesunięcie Lamba). Aby zharmonizować wyniki teorii z dokładniejszymi danymi doświadczalnymi na temat widma atomu wodoru, trzeba było zaproponować inne rozwiązania i podejścia niż te, które wynikały z wyprowadzenia równania Diraca.
Nowe podejścia teoretyczne nic nie dały i tylko uzupełniły teorię o nielogiczne i niefizyczne propozycje przezwyciężenia pojawiającej się osobliwości rozwiązań: renormalizację, skończoną różnicę nieskończoności z pożądaną wartością różnicy itd. Uwzględnienie wielkości jądra poprawiło tylko wartość Z na większą, ale nie rozwiązało problemu Z>137. Niesamowity wynik otrzymano również dla problemu atomu wodoru, że elektron znajduje się najprawdopodobniej w centrum atomu, czyli w jądrze.
Wyniki rozwiązania problemu dla cząstki w studni potencjału zarówno w przypadku równania Kleina-Focka-Gordona jak i równania Diraca są sprzeczne z podstawową zasadą mechaniki kwantowej, z zasadą nieoznaczoności. Z rozwiązań okazuje się, że cząstka może być w stanie związanym w studni o dowolnych wymiarach, w szczególności o rozmiarze znacznie mniejszym niż długość fali samej cząstki, A=ℏ/mc.
Pomimo, że Dirac sam zaproponował układ liniowych równań relatywistycznych pierwszego stopnia w reprezentacji macierzowej, które opisywały układ ze spinem 1/2, sprzeczności nie zniknęły, a on sam pozostał niezadowolony z wyników swojej teorii. Jak napisał Dirac w 1956 roku , rozwój relatywistycznej teorii elektronów może być teraz traktowany jako przykład tego, jak błędne argumenty prowadzą czasem do wartościowego wyniku. W latach 70. stało się jasne, że relatywistyczna teoria mechaniki kwantowej nie istnieje i należy poszukiwać nowych, fundamentalnych podejść i równań dla skonstruowania spójnej teorii relatywistycznej mechaniki kwantowej. A w latach 80-tych Dirac mówił już o nieprzezwyciężalnych trudnościach istniejącej teorii kwantowej i konieczności stworzenia nowej .
Przyczyna niepowodzenia tych teorii jest dość prosta – tkwi w ignorowaniu zależności energii oddziaływania z polem od prędkości cząstki. Uogólniony moment pędu układu cząstka plus pole zewnętrzne jest sumą relatywistycznego wyrażenia na mechaniczny moment pędu cząstki i moment pędu pola w przypadku oddziaływania z nieruchomą cząstką
co nie jest niezmiennikiem prędkości cząstki. Aby z takiej reprezentacji skonstruować jakiś niezmiennik, zastosowano we wszystkich przypadkach relację „niezmienniczą” w postaci różnicy pomiędzy uogólnionym pędem układu a pędem pola w przypadku oddziaływania z nieruchomą cząstką
Oczywiście, permutacja składowych uogólnionego momentu pędu dla konstrukcji niezmiennika nie rozwiązuje postawionego problemu. Stwierdzenie, że wyrażenie (20) jest mechanicznym momentem pędu cząstki i dlatego jest niezmiennikiem jest nieudowodnione i konieczne jest pojmowanie wzoru (20) jako empirycznego. Stąd, przy dużych prędkościach lub silnych oddziaływaniach, nieuwzględniona zależność energii oddziaływania cząstki z polem od prędkości ruchu cząstki, co prowadzi do błędnych wyników lub niemożności obliczeń.
W , zaproponowano niezmienniczą reprezentację uogólnionego pędu układu, w której uwzględniono zależność energii oddziaływania cząstki z polem od prędkości:
który jest czterowymiarową reprezentacją uogólnionego pędu układu opartą na wyrażeniu na uogólniony pęd nieruchomej cząstki w stanie spoczynku
którego niezmiennik jest zawsze równy wyrażeniu (19) niezależnie od stanu układu.
Zastosowanie zasad wariacyjnych do konstrukcji teorii relatywistycznej i kwantowej opierało się na zasadach konstrukcji mechaniki za pomocą Lagrangianu układu, który pierwotnie nie był przeznaczony dla podejść relatywistycznych. Konstrukcja Lagrangianu jest parametryczna z jedną zmienną czasową τ = ct, wyodrębnioną spośród zmiennych przestrzeni czterowymiarowej (pozostałe są reprezentowane przez zależność od tej zmiennej τ) i zawiera całkowitą różnicę względem tej zmiennej, czyli prędkość cząstki. Taka konstrukcja jest niedopuszczalna z powodu niemożności zastosowania zasady niezmienniczości reprezentacji zmiennych i kowariantnego odwzorowania działania układu.
W celu skonstruowania teorii relatywistycznej na podstawie zasad wariacyjnych rozważono kanoniczne (nieparametryczne) rozwiązania problemu wariacyjnego dla kanonicznie zdefiniowanych całek funkcyjnych i napisano kanoniczne rozwiązania problemów wariacyjnych mechaniki w przestrzeniach Minkowskiego. W wyniku unifikacji zasad wariacyjnych najmniejszego działania, przepływu i hiperprzepływu otrzymano kanonicznie niezmiennicze równania uogólnionego pędu. Z równań tych otrzymuje się wyrażenia na funkcję akcji i funkcję falową jako ogólne rozwiązanie zunifikowanego problemu wariacyjnego mechaniki.
Poniżej przedstawiamy uogólnioną zasadę niezmienniczości i odpowiadającą jej reprezentację uogólnionego momentu pędu układu, równania mechaniki relatywistycznej i kwantowej, podajemy rozwiązania problemów ruchu ładunku w stałym polu elektrycznym, problemów cząstki w studni potencjału i przejścia cząstki przez barierę potencjału, problemów ruchu w polu wykładniczym (Morse’a), problemów cząstki naładowanej w polu magnetycznym, a także problemy atomu wodoru.




