Vergelijkingen van Relativistische en Kwantum Mechanica (zonder Spin)
Inleiding
Aan alles twijfelen of alles geloven zijn twee even handige oplossingen;
beide maken reflectie overbodig.
Henri Poincaré (1854-1912)
Ik weet het, ik weet het, maar stel – stel nou eens! – dat de zuiverheid van de cirkel ons verblind heeft van het zien van iets daarbuiten!
Ik moet helemaal opnieuw beginnen met nieuwe ogen, ik moet alles opnieuw overdenken!
Hypathia (∼360-415 AD)
In 1913 construeerde Bohr, op basis van de empirische formules van Balmer, een atoommodel gebaseerd op de kwantisering van het baanmoment, dat later werd aangevuld met de meer algemene kwantiseringsregels van Sommerfeld. In die jaren werd natuurlijk niet uitgegaan van de aanwezigheid van een spin of een intrinsiek magnetisch moment van het deeltje of, vooral, spin-baan interactie, of interactie met de nucleaire spin.
In 1916 leidde Sommerfeld, in het kader van relativistische benaderingen, een formule af voor de energieniveaus van een waterstof-achtig atoom, zonder rekening te houden met de spin . Sommerfeld ging uit van het model van het Bohr-atoom en gebruikte de relativistische relatie tussen het momentum pand de energie E van een vrij deeltje met de massa m.
waar c de snelheid van het licht is.
In een extern veld met een vierdimensionale potentiaal (φ,A) werd verondersteld dat voor een deeltje met de lading qdeze relatie ook kan worden gebruikt als we de componenten van het vierdimensionale impulsmoment van het veld (qφ,qA) aftrekken van de uitdrukking voor het veralgemeende deeltjesmomentum:
In het geval van de Coulomb-potentiaal φ=Ze/r, waarbij e de lading van het elektron is, ris de afstand tot de kern, en Z een atoomnummer, verkrijgt men in bolcoördinaten
waar Lis het impulsmoment. De Bohr-Sommerfeld kwantisatievoorwaarden hebben de vorm
waar nφen nr respectievelijk de orbitale en radiale quantumgetallen zijn. Voor de energieniveaus verkreeg Sommerfeld de formule
waarbij het hoofdkwantumgetal n=nr+l+1=1,2,3,…, l=0,1,2,3,…,n-1, en α=1/137,036 de fijnstructuurconstante is. Echter, in een artikel gepubliceerd in 1916 , Sommerfeld “maakte een gelukkige fout” en de afgeleide formule werd gepresenteerd in de volgende vorm
De formule (6) beschreef perfect alle eigenaardigheden van de structuur van het spectrum van waterstof en andere soortgelijke atomen met de voor die jaren beperkende nauwkeurigheid van de metingen, en er was geen twijfel over de juistheid van de formule zelf. Daarom werd de Sommerfeld formule als empirisch opgevat, en in plaats van het kwantumgetal l werd een “mysterieus” intern kwantumgetal met half-integer waarden j=1/2,3/2,5/2,…,n+1/2werd geïntroduceerd, en formule (6) werd gebruikt in de voorstelling
waarbij n=nr+j+1/2=1,2,3,…,j=1/2,3/2,5/2,…,n+1/2, en l de waarden l=0 bezit bij j=1/2 en l=j±1/2 voor anderen. Deze formule valt samen met het resultaat van een exacte oplossing van de relativistische Dirac vergelijkingen in 1928 voor een deeltje met de spin 1/2 met de klassieke uitdrukking voor de potentiële energie van een onbeweeglijke lading in het Coulomb veld van een kern met een atoomnummer Zin de vorm Ur=Ze2/r.
Formule (7) gaf ook een vreemde beperking aan van de waarde de lading van een kern met het atoomnummer Z<137, waarboven de formule zijn betekenis verliest. Het was ook duidelijk dat binnen het kader van de geschetste benaderingen, de sterke en gravitationele interacties, de bewegingen van de planeten niet worden beschreven. Het probleem Z<137of α>1 blijft het onopgeloste probleem van de relativistische quantummechanica. Door de formule (7) uit te breiden over de machten Zα2 in de Taylorreeks, met een nauwkeurigheid van expansie tot de termen door de machten Zα6, verkrijgen we
In 1925-1926 werkte Schrödinger aan de afleiding van de vergelijking voor de golffunctie van een deeltje dat de De Broglie golven beschrijft. De afleiding van de vergelijking was ook gebaseerd op de relativistische relatie (1) tussen het momentum pand de energie E van het deeltje, die hij voorstelde met behulp van de operatoren van de kwadraten van energie en impuls in de vorm van een vergelijking voor de golffunctie
Zoals Sommerfeld, Schrödinger gebruikte de volgende voorstelling voor een deeltje in een extern veld
In het geval van stationaire toestanden van een geladen deeltje in het veld van de Coulombpotentiaal voor een waterstofatoom moest de vergelijking
Zoals men kan zien, dat de kwadratische uitdrukking van de potentiële energie q2φ2r/2mc2 met een positief teken in de vergelijking aanwezig is en dat in het geval van aantrekkende velden de oplossingen tot bepaalde moeilijkheden leiden. Bij het naderen van het singulariteitspunt nemen door het negatieve teken de aantrekkende krachten toe en de aanwezigheid van de singulariteit leidt tot bekende beperkingen van de grootte van de interacties (figuur 1).
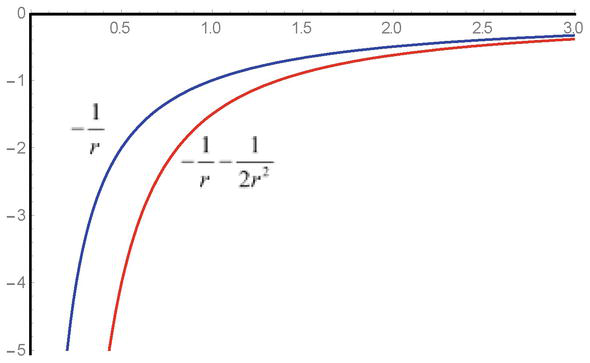
Figuur 1.
De singulariteitsafhankelijkheid van de attractieve veldpotentiaal-1/rand potentiële interactie-energie-1/r-1/2r2in de Klein-Gordon vergelijkingen.
Volgende, de golfvector kis voorgesteld als
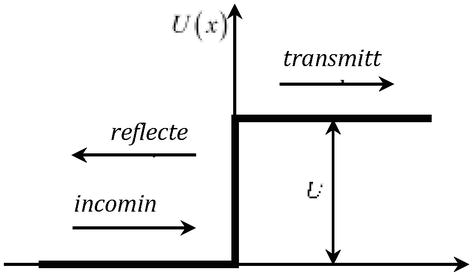
en wanneer men het probleem beschouwt van de passage van een deeltje met energie Eth door een potentiaalbarrière U=qφr(figuur 2), waarvan de hoogte groter is dan de verdubbelde rust-energie van het deeltje U>2mc2, wordt de transmissiecoëfficiënt eenparig, ongeacht de hoogte van de barrière (Klein paradox) .
Figuur 2.
Passage van een deeltje door een potentiële barrièreU.
Een andere moeilijkheid is dat, zoals de oplossing van het deeltjesprobleem in een potentiaalput laat zien, bij voldoende diepte een deeltje met een golflengte ƛ=ℏ/mcc gebonden toestanden kan hebben (gelokaliseerd kan worden) in een putbreedte die smaller is dan de golflengte van het deeltje d<ƛ/2(figuur 3), hetgeen in strijd is met het fundamentele principe van de kwantummechanica – het Heisenbergs onzekerheidsprincipe.
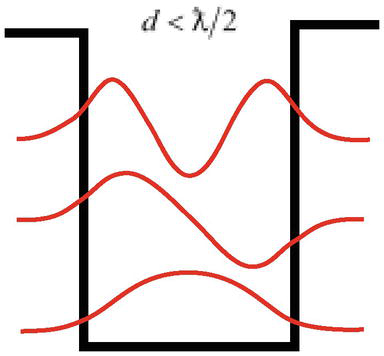
Figuur 3.
Een deeltje met een golflengteƛkan worden gelokaliseerd in een put met een breedted<ƛ/2.
Ook wordt de oplossing van het probleem van een waterstofachtig atoom beperkt door de waarde van het rangtelwoord van de atoomkern Z≤68 (voor de Dirac-vergelijking is de beperking van het atoomgetal Z≤137). Hetzelfde in de relativistische mechanica – wanneer men sterke wisselwerkingen beschouwt, geeft de oplossing van de relativistische vergelijking Hamilton-Jacoby de zogenaamde “deeltjesval op het centrum” aan.
Om de kwadratische term kwijt te raken of het teken ervan om te keren, heeft men de laatste jaren voorgesteld om de potentiële energie in de vergelijkingen Klein-Gordon en Dirac voor te stellen als het verschil van de kwadraten van de uitdrukkingen van de scalaire en vector potentialen (S-golf vergelijking). Een dergelijk wiskundig formalisme corrigeert de situatie, maar vanuit fysisch oogpunt zijn dergelijke voorstellingen geenszins gerechtvaardigd, en de velden die overeenkomen met dergelijke pseudo-potentiëlen bestaan niet in de natuur.
Het is nog erger met de aanwezigheid van een kwadratische term van het vectorveld, door het teken waarvan we in de natuur niet-bestaande toestanden krijgen en oplossingen die in tegenspraak zijn met de ervaring.
Volgens de oplossingen van de vergelijkingen van de kwantummechanica en Hamilton-Jacoby, blijkt dat een geladen deeltje in een magnetisch veld, behalve dat het in een cirkel draait, ook radiale trillingen-Landau-niveaus heeft (zelfs in het geval van nul orbitaal momentum).
In de loop van deze 90 jaar, vooral in zeer nauwkeurige cyclotronresonantie-experimenten, heeft niemand de radiale trillingen van het elektron en de Landau-niveaus gedetecteerd.
Het oplossen van deze vergelijking leverde Schrödinger, evenals Sommerfeld, de formule (5) op, die de structuur van het waterstofspectrum niet exact beschreef. Bovendien blijkt uit de oplossing van het probleem voor een deeltje in een potentiaalput, dat een deeltje met een golflengte ƛ=ℏ/mchas gebonden toestanden (wordt geplaatst) in een put van willekeurige grootte en, in het bijzonder, veel kleiner dan ƛ/2. Dit feit is in tegenspraak met het fundamentele principe van de quantum (golf) theorie, het principe van onzekerheid.
In 1925 stuurde Schrödinger dit werk naar de redactie van ‘Annalen der Physik’ , maar nam vervolgens het manuscript, weigerde de relativistische benaderingen en bouwde in 1926 een golfvergelijking gebaseerd op de klassieke Hamiltoniaanse uitdrukking, de Schrödinger vergelijking .
De vergelijking beschreef het spectrum van het waterstofatoom slechts kwalitatief, maar kende geen onredelijke beperkingen of singuliere oplossingen in de vorm van de Sommerfeld-Dirac formule. Klein , Fock en Gordon publiceerden in 1926 de relativistische vergelijking op basis van de golfvergelijking voor een deeltje zonder spin; deze wordt de Klein-Fock-Gordon vergelijking genoemd.
Met de ontdekking van de spin veranderde de situatie drastisch, en in 1926 toonden Heisenberg en Jordan aan dat, binnen de Pauli-beschrijving van de spin van een elektron, de helft van de energie van de spin-orbit interactie gelijk is aan een term met een macht van α4 in de Taylor-reeks uitbreiding van de Sommerfeld formule vergelijking referentie gaat hier.
Waarom precies de helft, Thomas probeerde dit in 1927 te verklaren door de aanwezigheid van een relativistische precessie van een elektron in het referentiekader van beweging langs de baan . De energie van de Thomas precessie is precies gelijk aan de helft van de waarde van de energie van de spin-baan wisselwerking met het inverse (positieve) teken, die bij de energie van de spin-baan wisselwerking moet worden opgeteld. De onjuiste veronderstelling dat de Thomas-precessiefrequentie in beide referentiekaders identiek is en het ontbreken van een gemeenschappelijke en correcte afleiding voor niet-inertiale (roterende) referentiekaders deden echter twijfels rijzen over de juistheid van dergelijke benaderingen. De reden voor het voorkomen van de helft van de energie van de spin-baan wisselwerking in de Sommerfeld formule wordt nog steeds onderzocht en is een van de onopgeloste problemen in de moderne natuurkunde.
Aan de andere kant, zowel in de afleiding van de Sommerfeld formule als bij de oplossing van de Klein-Fock-Gordon vergelijking voor het waterstofatoom probleem , werd aanvankelijk noch met de spin noch met de spin-baan wisselwerkingsenergie rekening gehouden. Daarom kan de verkregen fijne splitsing in geen geval te wijten zijn aan de spin-baan wisselwerking. Dit is een relativistisch maar zuiver mechanisch effect, waarbij de massa (traagheid) van een deeltje reeds afhankelijk is van de bewegingssnelheid langs de baan (van het impulsmoment), waardoor de radiale beweging van het elektron verandert, en omgekeerd. Juist deze afhankelijkheid, die leidt tot de splitsing van de energieniveaus van het elektron, en tot de onmogelijkheid er slechts één in te voeren, is het hoofdkwantumgetal. Niettemin, zelfs met deze veronderstelling, is de volgorde van splitsing van de niveaus volgens formule (8) in tegenspraak met de logica; het blijkt dat hoe groter het orbitaal impulsmoment, hoe kleiner de energie van het gesplitste niveau.
De matrixvoorstelling van de tweede-orde golf Eq. (9) door een stelsel vergelijkingen van de eerste orde is de Dirac constructie van de relativistische elektronenvergelijking (de Dirac matrices zijn de bijzondere representatie van de Clifford-Lipschitz getallen ). In de standaardvoorstelling heeft de Dirac-vergelijking voor een vrij deeltje de vorm .
waar
zijn de Pauli matrices (de eenheidsmatrix in de formules is weggelaten).
Voor een deeltje in een extern veld wordt Eq. (16) gewoonlijk geschreven in de vorm
waarbij voor een invariante voorstelling in het geval van een vrij deeltje de vergelijkingen zijn samengesteld voor het verschil tussen het gegeneraliseerde impulsmoment en het impulsmoment van het veld.
In het geval van de potentiële energie van een onbeweeglijke lading in een Coulomb-veld, verkrijgen wij de Sommerfeld-Dirac formule als resultaat van een exacte oplossing van deze bijzondere vergelijking. Ook daar wordt, hoewel voor een systeem met spin 1/2 de energie van de spin-orbit interactie in eerste instantie niet in aanmerking genomen, maar wordt de helft verkregen uit de exacte oplossing van het waterstofatoom probleem.
Nauwkeuriger metingen van Lamb in 1947 en latere verbeteringen in het spectrum van het waterstofatoom brachten aan het licht dat, naast de lijnen met de maximale j, ook alle andere lijnen gesplitst en enigszins verplaatst worden (de Lamb verschuiving). Om de resultaten van de theorie in overeenstemming te brengen met nauwkeuriger experimentele gegevens over het spectrum van het waterstofatoom, moest men andere oplossingen en benaderingen voorstellen dan bij de afleiding van de Dirac-vergelijking waren vastgelegd.
De nieuwe theoretische benaderingen hadden niets opgeleverd en vulden de theorie slechts aan met de onlogische en niet-fysische voorstellen om de opkomende singulariteit van de oplossingen te overwinnen: de renormalisatie, het eindige verschil van oneindigheden met de gewenste waarde van het verschil, enzovoorts. Het rekening houden met de grootte van de kern corrigeerde alleen de Z-waarde naar de grotere waarde, maar loste het Z>137-probleem niet op. Een ongelooflijk resultaat werd ook verkregen voor het probleem van het waterstofatoom dat het elektron zich hoogstwaarschijnlijk in het centrum van het atoom bevindt, dat wil zeggen in de kern.
De resultaten van de oplossing van het probleem voor een deeltje in een potentiaalput zowel in het geval van de Klein-Fock-Gordon vergelijking als van de Dirac vergelijking zijn in tegenspraak met het basisprincipe van de kwantummechanica, met het onzekerheidsprincipe. Uit de oplossingen blijkt dat een deeltje in een gebonden toestand kan zijn in een put met willekeurige afmetingen, in het bijzonder met de afmeting veel kleiner dan de golflengte van het deeltje zelf, A=ℏ/mc.
Ondanks het feit dat Dirac zelf een stelsel lineaire eerstegraads relativistische vergelijkingen in de matrixvoorstelling voorstelde dat het systeem met spin 1/2 beschreef, verdwenen de tegenstrijdigheden niet, en bleef hij zelf ongelukkig met de resultaten van zijn theorie. Zoals Dirac in 1956 schreef, kan de ontwikkeling van de relativistische elektronentheorie nu worden beschouwd als een voorbeeld van hoe onjuiste argumenten soms tot een waardevol resultaat kunnen leiden. In de jaren ’70 werd duidelijk dat de relativistische theorie van de kwantummechanica niet bestaat, en dat moet worden gezocht naar nieuwe, fundamentele benaderingen en vergelijkingen om een consistente theorie van de relativistische kwantummechanica te construeren. En in de jaren ’80, sprak Dirac reeds over de onoverkomelijke moeilijkheden van de bestaande quantumtheorie en de behoefte om een nieuwe te creëren.
De reden voor het falen van deze theorieën is vrij eenvoudig-het is in het negeren van de afhankelijkheid van de interactie-energie met het veld op de snelheid van het deeltje. Het gegeneraliseerde momentum van het systeem, het deeltje plus het externe veld, is de som van de relativistische uitdrukking voor het mechanische momentum van het deeltje en het veldmomentum in het geval van interactie met het onbeweeglijke deeltje
wat geen invariante weergave is van de snelheid van het deeltje. Om uit zo’n voorstelling een invariant te construeren, werd in alle gevallen een “invariante” relatie gebruikt in de vorm van een verschil tussen het veralgemeende momentum van het systeem en het veldmomentum in het geval van interactie met het onbeweeglijke deeltje
Het is duidelijk dat de permutatie van de componenten van het gegeneraliseerde momentum voor de constructie van de invariant het gestelde probleem niet oplost. De bewering dat de uitdrukking (20) het mechanisch impulsmoment van een deeltje is en daarom een invariant is, is onbewezen en het is nodig de formule (20) als een empirische te beschouwen. Daarom, bij hoge snelheden of sterke interactie, een onverklaarde afhankelijkheid van de energie van de deeltjesinteractie met het veld op de snelheid van de deeltjesbeweging, die tot de onjuiste resultaten of de onmogelijkheid van berekeningen leidt.
In werd een invariante voorstelling van het gegeneraliseerde momentum van het systeem voorgesteld, waarin de afhankelijkheid van de interactie-energie van het deeltje met het veld van de snelheid in aanmerking werd genomen:
die de vierdimensionale voorstelling is van het gegeneraliseerde momentum van het systeem op basis van de uitdrukking voor het gegeneraliseerde momentum van een onbeweeglijk deeltje in rusttoestand
waarvan de invariant altijd gelijk is aan de uitdrukking (19), ongeacht de toestand van het systeem.
De toepassing van variatieprincipes om de relativistische en kwantumtheorie te construeren was gebaseerd op de principes van de constructie van de mechanica met behulp van de Lagrangiaan van het systeem , die oorspronkelijk niet bedoeld was voor relativistische benaderingen. De Lagrangiaanse constructie is parametrisch met de ene tijdsvariabele τ = ct, uitgezonderd van de variabelen van de vier-dimensionale ruimte (de rest wordt vertegenwoordigd door de afhankelijkheid van deze variabele τ) en bevat het totale differentiaal ten opzichte van deze variabele, de snelheid van het deeltje. Een dergelijke constructie is onaanvaardbaar wegens de onmogelijkheid om het principe van invariantie van de vertegenwoordiging van variabelen en de covariante vertegenwoordiging van de actie van het systeem toe te passen.
Om de relativistische theorie op basis van variatieprincipes te construeren, zijn de canonieke (niet parametrische) oplossingen van het variatieprobleem voor canonisch gedefinieerde integrale functionalen beschouwd en zijn de canonieke oplossingen van de variatieproblemen van de mechanica in de Minkowski-ruimten geschreven. Door de variatieprincipes van kleinste actie, stroming en hyperstroming te verenigen, worden de canonisch invariante vergelijkingen voor het gegeneraliseerde momentum verkregen. Uit deze vergelijkingen worden de uitdrukkingen voor de actiefunctie en de golffunctie verkregen als de algemene oplossing van het verenigde variatieprobleem van de mechanica.
Hieronder stellen wij het veralgemeend invariantieprincipe voor en de overeenkomstige voorstelling van het veralgemeend impulsmoment van het systeem, de vergelijkingen van de relativistische en kwantummechanica, geven de oplossingen van de problemen van de ladingsbeweging in een constant elektrisch veld, de problemen voor een deeltje in een potentiaalput en de doorgang van een deeltje door een potentiaalbarrière, de problemen van de beweging in een exponentieel veld (Morse), de problemen van geladen deeltje in een magnetisch veld, en ook de problemen van een waterstofatoom worden gegeven.




