Svårtsekvationer i relativ- och kvantmekaniken (utan spinn)
Inledning
-Då tvivla på allting eller tro på allting är två lika bekväma lösningar;
båda gör att man inte behöver reflektera.
Henri Poincaré (1854-1912)
Jag vet, jag vet, men tänk om – bara tänk om! – cirkelns renhet har förblindat oss från att se något bortom den!
Jag måste börja om från början med nya ögon, jag måste ompröva allt!
Hypathia (∼360-415 e.Kr.)
1913 konstruerade Bohr, med utgångspunkt i de empiriska formlerna från Balmer, en atommodell som byggde på en kvantisering av orbitala rörelsemängden , som senare kompletterades med de mer generella Sommerfeld-kvantiseringsreglerna. Under dessa år antogs naturligtvis inte förekomsten av ett spinn eller ett inneboende magnetiskt moment hos partikeln eller, i synnerhet, spin-orbit växelverkan eller växelverkan med kärnans spinn.
År 1916 härledde Sommerfeld, inom ramen för relativistiska ansatser, en formel för energinivåerna hos en väteliknande atom, utan att ta hänsyn till spinnet . Sommerfeld utgick från Bohr-atomens modell och använde den relativistiska relationen mellan rörelsemängden och energin E hos en fri partikel med massan m.
där c är ljusets hastighet.
I ett yttre fält med en fyrdimensionell potential (φ,A) antogs det att för en partikel med laddningen q kan denna relation också användas om vi subtraherar komponenterna av fältets fyrdimensionella rörelsemängd (qφ,qA) från uttrycket för den generaliserade partikelrörelsemängden:
I fallet med Coulombpotentialen φ=Ze/r, där e är elektronens laddning, ris avståndet från kärnan och Zär ett atomnummer, erhåller vi i sfäriska koordinater
där Lis vinkelimpulsen. Bohr-Sommerfelds kvantiseringsvillkor har formen
varvid nφoch nrär orbitala respektive radiella kvanttal. För energinivåerna fick Sommerfeld fram formeln
där det huvudsakliga kvantantalet n=nr+l+1=1,2,3,…, l=0,1,2,3,…,n-1, och α=1/137,036är finstrukturkonstanten. I en artikel som publicerades 1916 gjorde Sommerfeld emellertid ”ett lyckligt misstag” och den härledda formeln presenterades i följande form
Formeln (6) beskrev perfekt alla särdrag i strukturen hos spektrumet hos väte och andra liknande atomer med den för dessa år begränsande noggrannheten i mätningarna, och det fanns inget tvivel om att formeln i sig var korrekt. Därför uppfattades Sommerfelds formel som empirisk, och i stället för kvanttalet l fanns ett ”mystiskt” internt kvanttal med halva heltalsvärden j=1/2,3/2,5/2,….,n+1/2infördes, och formel (6) användes i representationen
där n=nr+j+1/2=1,2,3,…,j=1/2,3/2,5/2,…,n+1/2, och l har värdena l=0 vid j=1/2och l=j±1/2för andra. Denna formel sammanfaller med resultatet av en exakt lösning av de relativistiska Dirac-ekvationerna 1928 för en partikel med spinn 1/2med det klassiska uttrycket för den potentiella energin för en orörlig laddning i Coulombfältet hos en kärna med atomnummer Zin i formen Ur=Ze2/r.
Formel (7) indikerade också en märklig begränsning av värdet på laddningen hos en kärna med atomnummer Z<137, över vilken formeln förlorar sin betydelse. Det var också uppenbart att inom ramen för de beskrivna tillvägagångssätten, den starka och gravitationella växelverkan, beskrivs inte planeternas rörelser. Problemet Z<137eller α>1förblir ett olöst problem inom den relativistiska kvantmekaniken. Genom att expandera formeln (7) över ordningen av potenser Zα2 i Taylor-serien, med en expansionsnoggrannhet upp till termerna av potenser Zα6, får vi
Under åren 1925-1926 arbetade Schrödinger med att härleda ekvationen för en partikelvågs vågfunktion som beskriver De Broglie-vågorna . Ekvationen baserades också på den relativistiska relationen (1) mellan partikelns impuls och energi E, som han presenterade med hjälp av operatörerna för energins och rörelsens kvadrater i form av en ekvation för vågfunktionen
Likt Sommerfeld, Schrödinger använde följande representation för en partikel i ett yttre fält
I fallet med stationära tillstånd av en laddad partikel i fältet för Coulombpotentialen för en väteatom var det nödvändigt att lösa ekvationen
Som framgår, Det kvadratiska uttrycket för den potentiella energin q2φ2r/2mc2finns i ekvationen med ett positivt tecken och i fallet med attraherande fält leder lösningarna till vissa svårigheter. När man närmar sig singularitetspunkten, på grund av det negativa tecknet, ökar de attraktiva krafterna och närvaron av singulariteten leder till kända begränsningar av interaktionernas storlek (figur 1).
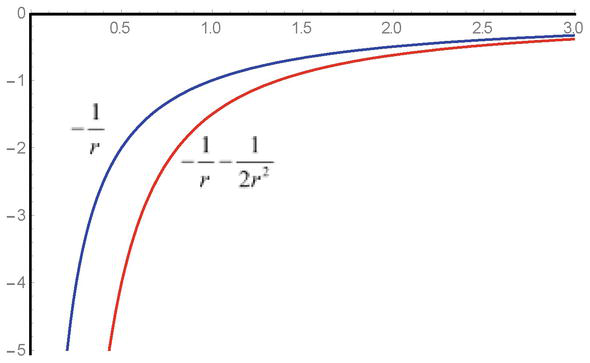
Figur 1.
Sampelberoendet av attraktionsfältspotentialen-1/och den potentiella interaktionsenergin-1/r-1/2r2i Klein-Gordonekvationerna.
Nästan, vågvektorn kis representeras som
och när man betraktar problemet med passagen av en partikel med energin Eth genom en potentialbarriär U=qφr(Figur 2), vars höjd är större än partikelns dubbla viloenergi U>2mc2, blir överföringskoefficienten enhetlig, oavsett höjden på hindret (Klein-paradoxen).
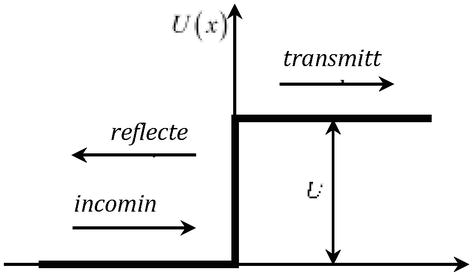
Figur 2.
Passage av en partikel genom ett potentiellt hinderU.
En annan svårighet är att, som lösningen av partikelproblemet i en potentiell brunn visar, på tillräckligt djup kan en partikel med en våglängd ƛ=ℏ/mccan ha bundna tillstånd (kan lokaliseras) i en brunnsbredd som är smalare än partikelns våglängd d<ƛ/2(figur 3), vilket strider mot kvantmekanikens grundläggande princip, Heisenbergs osäkerhetsprincip.
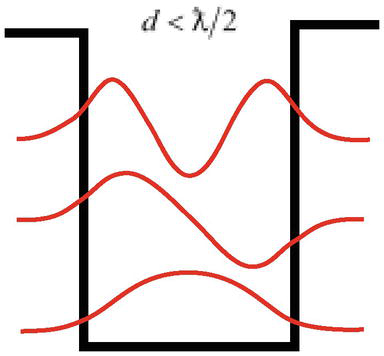
Figur 3.
En partikel med en våglängdƛkan lokaliseras i en brunnsbredd d<ƛ/2.
Också lösningen av problemet med en väteliknande atom begränsas av värdet på atomkärnans ordningsnummer Z≤68(för Dirac-ekvationen är begränsningen av atomnumret Z≤137). Samma sak i relativistisk mekanik – när man tar hänsyn till starka växelverkningar visar lösningen av den relativistiska Hamilton-Jacoby-ekvationen det så kallade ”partikelfallet i centrum” .
För att bli av med den kvadratiska termen eller vända på dess tecken har det på senare år föreslagits att representera den potentiella energin i Klein-Gordon- och Dirac-ekvationerna som skillnaden mellan kvadraterna av uttrycken för skalär- och vektorpotentialer (S-vågsekvationen) . En sådan matematisk formalism korrigerar situationen, men ur fysikalisk synvinkel är sådana representationer inte på något sätt motiverade, och de fält som motsvarar sådana pseudopotentialer existerar inte i naturen.
Det är ännu värre med närvaron av en kvadratisk term i vektorfältet, på grund av vars tecken vi får obefintliga tillstånd i naturen och lösningar som motsäger erfarenheten.
Enligt lösningarna på kvantmekanikens ekvationer och Hamilton-Jacoby, visar det sig att en laddad partikel i ett magnetfält, förutom att rotera i en cirkel, också har radiella vibrationer-Landau-nivåer (även i fallet med noll banmoment).
Under dessa 90 år, särskilt i mycket noggranna cyklotronresonansförsök, har ingen upptäckt elektronernas radiella vibrationer och Landau-nivåerna.
Som lösning på denna ekvation fick Schrödinger, liksom Sommerfeld, formeln (5), som inte exakt beskrev strukturen hos vätgasspektrumet. Dessutom, från lösningen av problemet för en partikel i en potentiell brunn, visar det sig att en partikel med en våglängd ƛ=ℏ/mchas bundna tillstånd (är placerad) i en brunn av godtycklig storlek och, i synnerhet, mycket mindre än ƛ/2. Detta faktum motsäger den grundläggande principen för kvant(våg)teorin, osäkerhetsprincipen.
In 1925 skickade Schrödinger detta arbete till redaktörerna för ”Annalen der Physik” , men tog sedan manuskriptet, vägrade de relativistiska tillvägagångssätten och byggde 1926 upp en vågekvation baserad på det klassiska hamiltoniska uttrycket, Schrödingerekvationen .
Ekvationen beskrev vätgasatomens spektrum endast kvalitativt, men den hade dock inga orimliga begränsningar eller singulära lösningar i form av Sommerfeld-Diracformeln. Klein , Fock och Gordon publicerade 1926 den relativistiska ekvationen baserad på vågekvationen för en partikel utan spinn; den kallas Klein-Fock-Gordon-ekvationen.
Med upptäckten av spinnet förändrades situationen drastiskt, och 1926 visade Heisenberg och Jordan att inom Pauli-beskrivningen av en elektrons spinn är halva energin i spinn-orbit-växelverkan lika med en term med en potens av α4 i Taylor-serieexpansionen av sommarfeldformeln ekvationsreferensen går här.
Varför exakt hälften, Thomas försökte förklara detta 1927 genom närvaron av en relativistisk precession av en elektron i referensramen för rörelse längs banan . Energin i Thomas precession är exakt lika med halva värdet av energin i spin-orbit växelverkan med omvänt (positivt) tecken, vilket bör läggas till energin i spin-orbit växelverkan. Det felaktiga antagandet att Thomas precessionsfrekvensen är identisk i båda referensramarna och avsaknaden av en gemensam och korrekt härledning för icke-inertiella (roterande) referensramar gav dock upphov till tvivel om riktigheten av sådana tillvägagångssätt. Orsaken till att halva energin för spin-orbitinteraktionen uppträder i Sommerfeldformeln undersöks fortfarande och är ett av de olösta problemen inom den moderna fysiken.
Å andra sidan togs varken spinnet eller energin för spin-orbitinteraktionen i beaktande från början, både vid härledningen av Sommerfeldformeln och vid lösningen av Klein-Fock-Gordon-ekvationen för väteatomproblemet . Därför kan den erhållna fina uppdelningen inte på något sätt bero på spin-orbit-växelverkan. Detta är en relativistisk men rent mekanisk effekt, när massan (trögheten) hos en partikel redan beror på hastigheten längs banan (vinkelmomentet), vilket gör att elektronens radiella rörelse förändras och vice versa. Just detta beroende, som leder till att elektronens energinivåer delas upp och att det är omöjligt att införa endast ett, det huvudsakliga kvantantalet. Ändå, även med detta antagande, strider ordningen för uppdelning av nivåerna enligt formel (8) mot logiken; det visar sig vara så att ju större orbitalt vridmoment, desto mindre energi i den uppdelade nivån.
Matrisrepresentationen av den andra ordningens våg Eq. (9) genom ett system av ekvationer av första ordningen är Dirac-konstruktionen av den relativistiska elektronekvationen (Dirac-matriserna är den särskilda representationen av Clifford-Lipschitz-talen ). I standardrepresentationen har Dirac-ekvationen för en fri partikel formen .
där
är Pauli-matriserna (enhetsmatrisen i formlerna utelämnas).
För en partikel i ett yttre fält gäller Eq. (16) vanligtvis skrivas i formen
där för en invariant representation i fallet med en fri partikel ekvationerna är sammansatta för skillnaden mellan det generaliserade momentet och fältets moment.
I fallet med den potentiella energin hos en orörlig laddning i ett Coulombfält får vi Sommerfeld-Dirac-formeln som ett resultat av en exakt lösning av denna speciella ekvation. Även där, även om det gäller ett system med spinn 1/2, beaktas inte energin i spinn-orbit-interaktionen inledningsvis, utan halva erhålls från den exakta lösningen av problemet med väteatomen.
Närmare Lamb-mätningar 1947 och efterföljande förbättringar av spektrumet för väteatomen avslöjade att förutom linjerna med det maximala j även alla andra linjer är uppdelade och något förskjutna (Lamb-förskjutningen). För att harmonisera teorins resultat med mer exakta experimentella data om väteatomens spektrum var man tvungen att föreslå andra lösningar och tillvägagångssätt än vad som fastställts genom härledningen av Dirac-ekvationen.
De nya teoretiska tillvägagångssätten hade inte gett något och kompletterade bara teorin med ologiska och icke-fysiska förslag för att överbrygga den framväxande singulariteten i lösningarna: renormalisering, ändlig skillnad av oändligheter med önskat värde på differensen, och så vidare. Genom att ta hänsyn till kärnans storlek korrigerades endast Z-värdet till ett större värde, men löste inte Z>137problemet. Ett otroligt resultat erhölls också för problemet med väteatomen, nämligen att elektronen med största sannolikhet befinner sig i atomens centrum, det vill säga i kärnan.
Resultaten av lösningen av problemet för en partikel i en potentiell brunn, både när det gäller Klein-Fock-Gordon-ekvationen och Dirac-ekvationen, står i motsättning till kvantmekanikens grundprincip, till osäkerhetsprincipen. Av lösningarna framgår att en partikel kan befinna sig i ett bundet tillstånd i en brunn med valfria dimensioner, i synnerhet med en storlek som är mycket mindre än partikelns egen våglängd, A=ℏ/mc.
Trots att Dirac själv föreslog ett system av linjära första gradens relativistiska ekvationer i matrisrepresentationen som beskrev systemet med spinn 1/2, försvann inte motsägelserna och han själv förblev missnöjd med resultaten av sin teori. Som Dirac skrev 1956 kan utvecklingen av den relativistiska elektronteorin nu betraktas som ett exempel på hur felaktiga argument ibland leder till ett värdefullt resultat. På 70-talet stod det klart att den relativistiska teorin för kvantmekaniken inte existerar, och att man bör söka efter nya, grundläggande tillvägagångssätt och ekvationer för att konstruera en konsekvent teori för den relativistiska kvantmekaniken. Och redan på 80-talet talade Dirac om de oöverstigliga svårigheterna med den befintliga kvantteorin och behovet av att skapa en ny .
Anledningen till att dessa teorier misslyckas är ganska enkel – den ligger i att man ignorerar beroendet av växelverkningsenergin med fältet av partikelns hastighet. Systemets generaliserade momentum, partikeln plus det yttre fältet, är summan av det relativistiska uttrycket för partikelns mekaniska momentum och fältets momentum vid växelverkan med den orörliga partikeln
vilket inte är en invariant representation av partikelhastigheten. För att konstruera någon invariant från en sådan representation användes en ”invariant” relation i alla fall i form av en skillnad mellan systemets generaliserade rörelsemängd och fältets rörelsemängd vid interaktion med den orörliga partikeln
Det är uppenbart att permutationen av komponenterna i det generaliserade momentet för konstruktionen av invarianten inte löser det ställda problemet. Påståendet att uttrycket (20) är en partikels mekaniska rörelsemängd och därför är en invariant är obevisat och det är nödvändigt att uppfatta formeln (20) som en empirisk. Vid höga hastigheter eller stark växelverkan uppstår därför ett oredovisat beroende av energin i partikelns växelverkan med fältet på partikelns rörelsehastighet, vilket leder till felaktiga resultat eller omöjliga beräkningar.
I , föreslogs en invariant representation av systemets generaliserade rörelsemängd, där beroendet av partikelns interaktionsenergi med fältet av hastigheten beaktades:
som är den fyrdimensionella representationen av systemets generaliserade rörelsemängd baserad på uttrycket för den generaliserade rörelsemängden hos en orörlig partikel i viloläge
dess invariant är alltid lika med uttrycket (19) oberoende av systemets tillstånd.
Användningen av variationsprinciper för att konstruera den relativistiska och kvantteorin baserades på principerna för konstruktion av mekaniken med hjälp av systemets lagrangian , som ursprungligen inte var avsedd för relativistiska tillvägagångssätt. Lagrangiankonstruktionen är parametrisk med den enda tidsvariabeln τ = ct, som är utpekad från variablerna i det fyrdimensionella rummet (resten representeras av beroendet av denna variabel τ) och innehåller den totala differensen med avseende på denna variabel, partikelns hastighet. En sådan konstruktion är oacceptabel på grund av omöjligheten att tillämpa principen om invarians i representationen av variablerna och den kovarianta representationen av systemets verkan.
I , för att konstruera den relativistiska teorin på grundval av variationsprinciper, har de kanoniska (icke-parametriska) lösningarna av variationsproblemet för kanoniskt definierade integralfunktionaler betraktats och de kanoniska lösningarna av mekanikens variationsproblem i Minkowskirummen har skrivits. På grund av att man förenar variationsprinciperna för minsta verkan, flöde och hyperflöde erhålls de kanoniskt invarianta ekvationerna för det generaliserade rörelsemängden. Från dessa ekvationer erhålls uttrycken för aktionsfunktionen och vågfunktionen som den allmänna lösningen på mekanikens enhetliga variationsproblem.
Nedan presenterar vi den generaliserade invariansprincipen och motsvarande representation av systemets generaliserade rörelsemängd, ekvationerna för relativistisk mekanik och kvantmekanik , ger lösningarna på problemen med laddningsrörelse i ett konstant elektriskt fält, problemen för en partikel i en potentiell brunn och passagen av en partikel genom en potentiell barriär, problemen med rörelsen i ett exponentiellt fält (Morse), problemen med en laddad partikel i ett magnetiskt fält, samt även problemen med en väteatom ges.




